|
РусАрх |
Электронная научная библиотека по истории древнерусской архитектуры
|
Источник: Афанасьев К.Н. Опыт пропорционального анализа. М., 1998. Все права сохранены.
Размещение электронной версии в открытом доступе произведено: http://piramyd.express.ru. Все права сохранены.
Иллюстрации приведены в примечаниях.
Размещение в библиотеке «РусАрх»: 2007 г .
К.Н. Афанасьев
Опыт пропорционального анализа
Книга К.Н. Афанасьева содержит существенно важные для архитектурной математики суждения и данные. Во введении, названном "Об архитектуре и математике. О соразмерности и пропорции" установлены основные рассматриваемые понятия. Во второй главе "Хасира, зодчий Древнего Царства Египта" автор предлагает анализ египетского рельефа, изображающего зодчего Древнего Египта, как пример пиктографического письма, несущего значительный объем математикой информации. Во второй главе "Парфенон и Эрехтейон. Античный ордер и канон Поликлета" речь идет об анализе пропорций этих памятников с помощью обнаруженного автором "канона Поликлета". В третьей главе "От Парфенона до Софии Киева и Новгорода" предлагается анализ ансамбля афинского Акрополя и устанавливается последовательная связь архитектурной теорий Древнего Египта, Античной Греции и Рима, Византии и Киевской Руси.
Об архитектуре и математике, о соразмерности и пропорции
Математика для творческого труда архитектора издавна признается чем-то очень важным, необходимым и плодотворным. И все же архитектурная наука так до сих пор и не разработала должным образом этот, можно сказать, кардинальный вопрос теории. Речь идет не только о ремесленном или техническом вооружении зодчего, о реализации идеи в проекте и сооружении, но и о творческом процессе поиска, о «формах» самой идеи, о «формах» художественного мышления. Мы далеки еще от создания строгой теории гармонизации архитектурной формы. В настоящее время необходимо хотя бы накопить и привести в должный порядок уже имеющиеся у нас данные, полученные в результате анализа архитектурной формы памятников исторического прошлого. За длительный период человеческой цивилизации создано немало произведений исключительной красоты. Эти произведения могут явиться примером использования зодчим в своем творческом труде математических закономерностей. Памятники архитектуры, получившие широкую известность как образцы пропорциональности и гармонии, буквально пронизаны математикой, целочисленными расчетами и геометрией. Таковы: пирамиды Египта, Парфенон и другие храмы античности, София Константинопольская, Джвари в Грузии, церковь Покрова на Нерли... Наши усилия в данном случае направлены на накопление данных аналитических исследований, без претензии на завершенную теоретическую систему мыслей и наблюдений. Но все же, прежде чем обратиться к аналитическим исследованиям, необходимо сделать несколько предварительных замечаний. Простое единичное, да и не только простое - всякое сложное число, - результат измерения, является количественным показателем. Речь идет о сравнении с эталоном, будь то антропометрические данные: палец, пядь, локоть или иные установленные общественным опытом меры длины. Отношение чисел (размеров) устанавливает соразмерность элементов. Пропорция - это равенство, или «соразмерность соразмерностей». И далее гармония - цепочка пропорций - своеобразная мелодия, охватывающая все произведение и устанавливающая пропорциональность целого. Таково краткое и в некоторой мере условное значение терминов, широко используемых нами в последующем изложении. Когда речь идет об искусстве архитектуры, то количественные методы познания имеют ограниченное значение. Архитектура не измеряется величиной - количественными показателями, простым измерением формы. Определение же соразмерностей в отличие от измерения является актом, подготовляющим ее к качественной оценке. Измерение (или размер) - это количественная категория, а результат соизмерения (или соразмерность) - в какой-то мере качественная. И измерение, и соизмерение оформляются на языке математики. Качественность соразмерности устанавливается и понимается в связи с ее смыслом, значением, обусловленностью. Прочность обеспечивается опытом, облеченным в математическую "форму": удобство определяется габаритами, установленными динамикой деятельности человека и также выражается языком математики. Художественность конструктивной и функциональной деятельности обусловлена стремлением созидающей воли к совершенству. Искусство занято «прочтением» закономерностей мира - космоса, природы, человека и тем самым его произведения обусловлены не только сущностью созидаемого объекта, что присуще дизайну, но и той информацией, которую творец - художник сумел увидеть и понять в окружающей его среде. Такие произведения, обращенные к чувствам и разуму человека, обогащают его жизненный опыт и формируют его мировоззрение. Возможна ли количественная оценка качества? И какая роль в этом случае пришлась бы на долю математики? Суждения по этим вопросам были бы небезынтересны. В настоящее время в области искусства, преимущественно архитектуры, делаются попытки вое шире и шире использовать математические методы, но до сих пор оценка качества произведений искусства удобными для измерения количественными категориями, оказывается для современной науки непосильной. На помощь приходит не число, оформляющее процесс измерения, а соразмерность и пропорция. В них выражаются качественные характеристики произведения, но опять же не в виде соразмерности и пропорции самих по себе, т. к. и они являются той же абстрактно-математической категорией, а постольку, поскольку они оформляют сравнение однородных взаимосвязанных по смыслу и значению явлений. Число, отношение, пропорция - это математические понятия, носящие абстрактный характер, но зачем они нам, эти понятия, если бы за ними не было породившего их опыта многообразной жизни. Однако, как непосильно для арифметики сложение разных именованных чисел, так же невозможно сопоставление, соизмерение разнородных элементов, складывающихся в произведение искусства. Нельзя искать математического выражения для всех элементов композиции, великое множество вопросов, в том числе и соразмерности и пропорции решаются интуицией, или искусством. Качественная оценка очень трудна для искусства. Оказываются совершенно неуместными методы сравнения, основывающиеся на усредненных показателях. Если море глубокое, а река мелкая, то это не значит, что корабли следует строить в расчете на усредненную величину. Методы экстраполяции так же нельзя признать пригодными и надежными для оценки произведения искусства. Нельзя обобщающую оценку явления определять как механическую сумму оценок его элементов. Как правило, среди множества элементов композиции имеются несколько главных формообразующих, определяющих ее, часто вопреки многим другим немаловажным соображениям. Например, город Венеция сооружен вопреки важнейшим градостроительным законам, но все же он прекраснейший город мира. Надо согласиться с тем, что экспертная оценка произведения, основанная на интуиции знатоков своего дела, является наиболее естественной и надежной. Этот метод подразумевает не оценку по элементам (или факторам), а композиции в целом. Композиция в ее законченном виде имеет почти обязательно новое по отношению к ее элементам качество, которое нельзя предугадать исходя из анализа «анатомических» подробностей. Не следует ли признать метод оценки, основавший на интуиции экспертов и находящийся вне пределов анализа и точного эксперимента, имеющим большое самостоятельное значение и право на существование? Это не значит, что первичный количественный анализ явления не должен занимать наше внимание. Напротив, цветы растут на вскопанных грядках. Математика является языком, методом оформления анализа, обобщения и прогнозирования. Но не следует во всем полагаться только на математические выкладки, хотя все виды познания мы стремимся совершенствовать и подготовлять к математическим формам выражения, которые, в свою очередь, в порядке «обратной связи» диктуют определенный характер проводимых исследований. И все же каждый предмет имеет свои неподверженные математизации законы развития, осмыслять которые бывает необходимо вне точных измерений. Вступая, казалось бы, в противоречие с ранее высказанными мыслями, можно предположить, что если разные объекты исследования, измеренные разными мерами, соизмеряются одними и теми же пропорциональными характеристиками, то они будут все же в чем-то, пусть с очень большой степенью обобщения, соответствовать друг другу. Эта мысль будет выглядеть чрез меру парадоксально и даже нелепо, если мы вздумаем сопоставлять в принципе несравнимое. Но один и тот же пропорциональный строй может в чем-то очень важном сопоставить и даже сроднить столь различные вещи, как, например, египетские пирамиды с холмами и даже горными образованиями; или колонны греческого дорического или ионического ордера с фигурой человека. В этом случае возникают ассоциативные связи - важнейший, хотя порой и неосознанный источник образной характеристики произведения архитектуры. Смысл, идея произведения, ассоциативные связи, метафора, конечно, рождаются в каждую историческую эпоху из суммы сложных этических, моральных, философских общественных взглядов, а короче и точнее - основаны на мировоззрении человека. Гармонические особенности произведения» как мы уже сказали, нельзя рассматривать в отрыве от идеи произведения, однако они коренятся в какой-то мере и в физиологических особенностях человеческого восприятия. Математическая характеристика физиологического механизма (органов чувств) является подосновой гармонизации формы, как в архитектуре и живописи, так и в музыке... Однако восприятие гармонии произведения искусства отнюдь не ограничено физиологическим процессом, оно сопричастно творчеству. Чем глубже проникаешься особенностями творческого процесса, тем произведение понятнее. Соприкосновение с большим искусством воспитывает эстетические чувства человека. Восприятие произведения - не пассивный процесс; сопереживание - сопоставление идеи произведения с мировоззрением, формирующим идеалы зрителя, - процесс творческий. Таким образом, и создание произведения искусства, и активное восприятие его, - творчество. Математика существует самостоятельно как бы вне собственно научного исследования, а равно и художественного творчества. Она является неизменным, обязательным «орудием» или даже своего рода «методом» (затрудняюсь сказать точнее), вооружающим исследователя, ученого или художника, придавая «форму» и конкретность нашим знаниям. Однако ее абстрактный характер не может служить основанием к абсолютизации ее значения. В такого рода ошибке гнездится формалистическое истолкование архитектурной формы. Используя математические методы для формирования наших наблюдений, нельзя забывать о возможности того, что в самой природе, вне нашего сознания, коренятся математические законы формообразования. Вполне естественно возникает вопрос, является ли математика продуктом чистого абстрактного мышления, вооружающим человека для познавательной и творческой деятельности или математический характер закономерностей - свойство формотворчества самой природы, а художник или естествоиспытатель эти закономерности улавливает и изучает? Умеет ли природа считать? Ответить на такой парадоксально поставленный вопрос - дело философов... По-видимому, человеческий гений оттачивает орудие познания - математику, а в природе есть что изучить при помощи такого «орудия». Об этом свидетельствуют геометрические закономерности космоса, рисунок цветов, пропорциональность фигуры человека и многое другое. Наличие гармонии в природе подтверждается пением птиц; от музыкального сочетания звуков даже собаки приходят в нервное состояние. Но ни птиц, ни собак нельзя удивить красотой произведения архитектуры. Восприятие музыкальной гармонии в известной степени может быть отнесено за счет биологических свойств органов слуха. Восприятие гармонии архитектурных форм, очевидно, далеко не в такой же степени объясняется строением человеческого глаза. Восприятие гармонии в изобразительных искусствах необходимо отнести к тренированному, воспитанному опытом человеческому сознанию. В богатейшей информации, полученной человеком посредством глаза, необходимо разобраться, для этого человек сопоставляет пространство и предметную среду, иначе говоря, измеряет их. Очень трудно найти соответствие закономерностям в произведениях искусств, на которых основывается гармонизация их форм, с законами формообразования в природе. Возможно, именно это соответствие, которое с очень скромными успехами настойчиво ищет художник, упорно ускользает от научного анализа. По средствам математических закономерностей вне ассоциативного мышления, вне мировоззрения, психологии человека... невозможно даже пытаться решать художественные задачи. Нельзя забывать об условиях формообразования, имеющих в основе образное мышление, причем математические методы сохраняют значение способа реализации идеи, даже если проблемы гармонизации формы не возникают или не ставятся вовсе. Рассматривая творческий процесс работы современного нам архитектора, мы встречаемся очень часто, быть может, в подавляющем числе случаев, с решением задачи соразмерностей и формы без каких-либо математических построений. Мы имеем в виду своего рода «интуитивно-рисовальные» методы творчества, которые могут быть особенно эффективными при решении сложных, заново поставленных задач, и предлагать композиционно интересные решения. Современная изобразительная техника значительно превосходит возможности изображения проектируемого сооружения в прошлом, что и формирует творческий метод современного зодчего. Ни в коем случае не отказываясь от достижений современной изобразительной техники и «рисовальных» методов работы зодчих, следует все же отдать себе отчет в том, что по своим музыкально гармоническим достоинствам зодчество далекого прошлого несомненно превосходит достижения современной архитектуры. Оба метода, как «математический», так и «рисовальный», находятся в тесном взаимодействии. Мы даже достаточно много говорим о рисовании геометрией при помощи простейших геометрических приемов, об альбоме Виллара де Гоннекура(1), заполненном множеством такого рода рисунков. Но можно говорить и, наоборот, о геометрических построениях на основе рисунка... На оба метода в разных модификациях искусство архитектуры опиралось всегда. Они служили не только целям оформления, но и поискам самой идеи произведения. В данном сборнике мы останавливаемся на примерах, характеризующих рабочий метод художника - зодчего, относящийся к отдаленному историческому прошлому. Актуальность этой проблемы заключается в том, что искусство прошлого существует и для современного человека отнюдь не в качестве мертвых музейных экспонатов, а живых волнующих произведений искусства, хотя и родившихся в Древнем Египте, античной Греции и, более того, в пещере Альтамира. Знакомство с элементами - частями целого и даже очень глубокое и тщательное изучение их дает относительное представление о целом. Умение понять целое, обобщить и соподчинить друг другу частности - особое свойство человека - художника. На каждом «уровне» суждений возникает новый смысл, новые качественные наблюдения. В некотором родстве с этим свойством интеллекта стоит интуиция - способность суммировать все многообразие жизненного опыта, что не может осуществить никакой точный расчет. Механика интуиции для нас до сей поры таинственна. Несомненно все же, что опыт является ее основой. Но о прямой пропорциональности опыта и интуиции не может быть речи. Более того, иной раз перенасыщенность знаниями и опытом служит для интуиции помехой. Интуиция, ассоциативное и образное мышление на своей начальной фазе обходится без математики, но оформление итогов творческого процесса без опоры на математику просто невозможно, по крайней мере, если речь идет о созидательной архитектурной деятельности. Искусство воспитывает и развивает чувственный аппарат человека и оно же приводит в порядок образное богатство природы, делая ее доступной или «удобной» для восприятия. В этом процессе математическое оформление играет очень важную роль. В поэзии, а также в музыке строгие ритм и такт подобны биению сердца и дыханию. Это и есть основа музыкальной и поэтической формы, а для архитектуры этой основой служит соразмерность и пропорциональность. Однако выразительности и экспрессии архитектура может достичь вовсе не обязательно средствами гармонии и пропорциональности. Современная архитектура ищет предельного эффекта и в этих целях она оперирует бессодержательными геометрическими формами и совсем не нуждается ни в их соразмерности, т. к. они бессодержательны, ни в пропорциональности. Ей становится чуждо само понятие гармонии. Гармония и пропорциональность произведения предполагает в зрителе определенный интеллектуальный уровень. Необходимо понять и почувствовать внутреннюю логику архитектуры. Понять архитектуру, следующую закономерностям природы космоса, ищущую общественный идеал прекрасного, можно чувством и разумом. Творчество вне всяких закономерностей может лишь удивить. Стремление к крайне экспрессивной форме вряд ли следует признать тенденцией с большим будущим. Экспрессивность, рассчитанная не на думающего и тонко чувствующего зрителя, быть может, способна возбудить сильные, но поверхностные эмоции. В архитектуре утонченность композиции, изысканность гармонического строя и сила эмоционального воздействия очень часто не совпадают и даже находятся в противодействии. Быть может не стоит обращать так много внимания на гармонические основы шедевров архитектуры исторического прошлого, имея ввиду современные тенденции в творчестве архитекторов? Если бы это было так, то все наши усилия были бы напрасны.
Хасира, зодчий Древнего Царства Египта
Сведения, которыми мы располагаем о древнем Египте, получены в весьма значительной степени из ознакомления с множеством рельефных изображений. Эти рельефы в изобилии покрывали стены и колонны древних гробниц и храмов. Они относятся ко всем периодам истории Египта: Древнему, Среднему и Новому Царствам, встречаются также и в позднее время. Они обладают качеством стойкой стилистической формы и в египетском искусстве занимают весьма важное место. Смысл множества рельефных изображений заключается, прежде всего, в их "информативности", или повествовательности, что играло большую роль, имея в виду особенности погребального и религиозного культа. Это было пиктографическое письмо очень высоких достоинств.
Изучая эти рельефные изображения, мы знакомимся буквально со всеми сторонами жизни Египта: хозяйственной деятельностью, организацией строительных работ, охотой и рыболовством, бытом, социальной характеристикой общества, а также важнейшими историко-политическими событиями. Рельефы Египта - подлинная энциклопедия жизни древнейшей цивилизации. И очень важно, что решение "утилитарной" задачи оказалось сопряженным с эстетическими композиционными закономерностями.
Письменность посредством рисунков была древнейшим способом передачи информации, она предшествовала письму иероглифами, которые обозначали отдельные слова и понятия. Это была письменность, еще не имевшая отношения к передаче звуковой речи. Вслед за тем следующим этапом развития явились иероглифы, означающие отдельные слоги. Слогов значительно меньше, чем слов - письменность становилась проще. И вот здесь-то пролегает рубеж развития письменности. Человек воспроизводит уже не события, не образы, а ищет обозначения звуков, сначала слогов, а затем и отдельных букв. Рождается буквенный алфавит.
Алфавит - одно из важнейших изобретений человека, лишь при помощи букв оказалось возможным письменно "воспроизводить" речь человека и в свою очередь оказывать влияние на формирование языка. Но одновременно алфавитная письменность утеряла замечательное свойство пиктографии быть понятной разноязычным народам, к тому же не умудренным грамотой. Буквенная письменность явилась, быть может, одним из факторов, приведших к разобщенности языка и культуры соседствующих групп населения.
Приходит на ум, что библейская легенда о "разноязычии", взаимном непонимании народов Вавилонии, строивших башню как символ мирового господства, имела в виду складывавшуюся в ту пору алфавитную клинопись (признаем, однако, что это замечание не имеет серьезного исторического основания).
Но не следует "скидывать со счетов" возможность дальнейшего развития по своим путям пиктографического письма вслед за рождением алфавита, воспроизводящего отдельные звуки. Человек верхнего палеолита овладевает техникой изображения. Он изображает, что видит и по возможности, как видит. Это в принципе реалистическая живопись с оттенком импрессионизма. Замечательная роспись сводов пещеры Альтамира по своему значению для истории живописи можно приравнять разве что плафону Сикстинской капеллы. Неолит ознаменован рождением изображения-знака, порождающего пиктографию. Дальнейшее развитие - это иероглиф-слово, иероглиф-слог, иероглиф-буква. Но эволюция собственно пиктографии не останавливается. В самом деле, в той или иной степени информация присутствует в любом произведении изобразительного искусства на всех этапах.
Таким образом, основная идея пиктографического письма - передача сведений при помощи изображений - остается в немалой степени целью изобразительного искусства. Художественное качество изображений во взаимоотношении с идеей произведения, с точки зрения его "информативности", делает искусство зеркалом общественного сознания.
Можно проследить пути развития пиктографии вплоть до стенописи в византийских и русских храмах, серий гравюр Дюрера, Хогарта, Гойи или даже таких единичных (вне серии) композиций, как, например, "Сватовство майора" П. Федотова, которая может быть приравнена к целому повествованию. Даже немое кино - по идее, динамическое пиктографическое письмо в своем предельном развитии.
Во всех этих росписях, гравюрах, живописных произведениях ведется рассказ или, как любят говорить теперь, предлагается "информация" об античных мифах, о евангельских или библейских событиях в последовательных эпизодах с анализом психологических переживаний, дается социально-бытовая характеристика семьи или изображение сцены, подобной театральной, что сближает творчество художника с работой драматурга и режиссера.
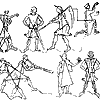
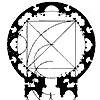
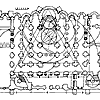
Древним звеном пиктографии, развивающимся параллельно иероглифическому письму, является культура древнеегипетского рельефа. Эти рельефы по характеру являются своего рода монументализированным рисунком, он отнюдь не многословен, все в нем подчинено идее повествования. Художник не стремится к изображению окружающего его мира, он не озабочен изображением пространства как такового, он не интересуется перспективными построениями. Можно думать, что не слишком мудреная система линейной перспективы просто была вне внимания египетского художника. Перспектива не была ему необходима... Художник не изображает предмет, как его можно увидеть, а повествует о нем, желая дать возможно более полную информацию. Информативность изображений достигается абстрагированием методов его начертания. Он руководствуется выработанными длительным опытом канонами и образцами, а главное - методами изображения. Например, человек изображается одновременно в профиль и фронтально. Глаз человека - прямо. Голова - в профиль, плечи развернуты также фронтально, ноги - снова в профиль. Условность изображения совершенно очевидна, но информацию о человеке мы получаем таким образом гораздо более достоверную, чем рассматривая объект наблюдения в перспективе и ракурсе. В самом деле, по изображению архитектора Хасира (иначе Сира-ха) можно ему купить шляпу нужного размера, сшить костюм и купить ботинки! Перед нами своеобразный чертеж-изображение человека и его размерная и пропорциональная характеристика (илл. 1 ).
Вспомним архитектурные чертежи недавнего прошлого (ХVI-ХVII веков), которые делались вне правил начертательной геометрии, архитектор решал стоящие перед ним задачи, совмещая планы с фасадами... Современный нам архитектор, проектируя, чертит строго в ортогональных проекциях. На этих чертежах решаются задачи соразмерности и пропорциональности. На их основе осуществляется строительство. Перспективный вид и даже модель здания не могут заменить такой чертеж.
Отметим, что египетские рельефы почти всегда сопровождаются пояснительными текстами, эти иероглифы композиционно тесно с ними скомпонованы. Это лишний раз свидетельствует об их близком родстве.
Пиктография продолжает жить и в наши дни, ее идея не утратила своего значения и кто знает, какова ее дальнейшая судьба.
Информация, которую дает произведение искусства, может быть самой различной. Прежде всего, речь идет об изображении предметов, их форме и соразмерности, затем о предметах во взаимодействии, различных событиях, бытовых, хозяйственных, производственных сценах и многом другом. Для рассказа об этих подчас очень сложных для изображения и понимания сюжетов оказалось необходимым выработать канонические приемы изображения, а, следовательно, и композиции. Законы соразмерности изображаемого предмета обусловливают соразмерности в сюжете, что, в свою очередь, приводит к закономерному композиционному построению целого. Все это становится ясным при анализе рельефного изображения Хасира, вооруженного профессиональным инструментом (жезлами) и сопровождаемогопышной титулатурой, написанной иероглифами, немало украшающими композицию(2).
Древнеегипетский рельеф является примером пиктографического письма в его изысканном развитом виде, в котором информативность сочетается с математическим расчетом изображения и всей композиции наряду с канонической формой и строгой соразмерностью частей. К тому же, несмотря на столь жесткие рамки творчества, а может быть в каком-то смысле и благодаря им, художник добивается удивительно тонкой нюансировки рисунка. Это свидетельствует о его высоком мастерстве и наблюдательности. Синтез этих качеств обеспечивает своеобразие, гармонические достоинства древнеегипетского рельефа.
Пропорциональный геометрический анализ произведений не только архитектуры, но и изобразительного искусства давно привлекает внимание исследователей. Речь идет равно как о пропорциональном каноне идеальной человеческой фигуры, о чем неизменно заботились художники Египта, Греции, раннего Средневековья, эпохи Возрождения, так и о композиционных закономерностях самого произведения, о гармонизации формы изображения и закономерностях композиции. Изобразительное искусство как бы сближается с архитектурной формой и композиция у обоих искусств подчиняется единым законам гармонии.
Однако в отличие от архитектора, рисуя, художник опирается на некий пропорциональный "каркас" изображения, а не на геометрическую форму изображаемого предмета. Это отлично иллюстрируется изображениями широко известного альбома средневекового мастера, архитектора и художника Виллара де Гоннекура. Геометрические схемы, положенные в основу изображений, не обозначают их форму. Это своего рода "триангуляция", которая определяет самые общие закономерности и "организует" рисунок. К такого же рода приемам начертания рисунка обращаемся и мы, анализируя изображение Хасира.
Для "разбивки" сооружения в натуре при его возведении необходимы измерительные приборы. В наше время это рулетка, нивелир и теодолит.
Древнеегипетский, античный и средневековый зодчие действовали при помощи шнура, позволявшего осуществлять "разбивку" сооружения, опираясь на классическую геометрию построения при помощи циркуля и линейки. Во время строительных работ эти инструменты заменяли натянутым шнуром (линейка) и тем же шнуром, закрепленным одним концом при помощи вбитого в грунт колышка (циркуль).
Но далеко не всякое геометрическое построение удобно производить на месте строительства в масштабах иногда значительных по размеру сооружений. В этих случаях осуществлялись построения, при помощи заранее изготовленных масштабных реек, или "жезлов".
Б. А. Рыбаков указывает в своих исследованиях и докладах на древние сказания о кентавре, или в русских текстах "китоврасе", олицетворяющем профессию зодчего, и обращает наше внимание на четыре "жезла", которыми он вооружен. Эти жезлы, как указывает автор, служили целям перенесения "в натуру" необходимых соразмерностей(3). Эти своеобразные измерительные линейки, по-видимому, заготовлялись зодчим для возведения проектируемого им здания, а может быть они имели универсальный характер и использовались при строительстве многих сооружений.
Размышляя о том, каких размеров были эти «жезлы китовраса», мы можем предположить, что один из них был равен пяди или футу или иной основополагающей мере длины. Другой жезл приравнен диагонали квадрата со стороной, равной первому жезлу, третий находился в отношении золотого сечения или его "функции", а четвертый, быть может, находился с первым жезлом в соотношении высоты равностороннего треугольника и его стороны. Эти соотношения размеров жезлов китовраса нами названы как возможные, и настаивать на том, что именно эти отношения и никакие другие использовались мудрым китоврасом во всех случаях, никак нельзя.
Ознакомившись в подлиннике в Каирском музее с прекрасно сохранившимся рельефом по дереву эпохи Древнего Царства, изображающим зодчего Хасира, мы обращаем внимание на то, что он "вооружен" тремя жезлами и специальным чернильным прибором(4).
Невольно приходит в голову предположение, что это и есть жезлы, которые служили ему для разбивки сооружений на месте и определения его соразмерностей - своего рода рулетка древнеегипетского зодчего.
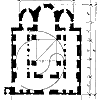
В портрете Хасира в полном соответствии с традициями египетского искусства мы встретились с ортогональностью изображения, дающей основание надеяться на возможность его масштабного измерения (схема соразмерностей 1).
Хасира держит в левой
руке большой и малый жезлы и письменный прибор. По поводу абсолютных размеров
большого жезла можно только гадать. Сравнивая его с возможным ростом зодчего,
можно предположить, что этот жезл имел размер примерно 135-
У нас нет необходимых
знаний, чтобы углубляться в метрологический анализ, заметим лишь, что размер
жезла не измеряется целым числом локтей - мах (
Большой жезл, в котором мы хотели бы видеть измерительную рейку, может быть просто посохом, с которым мы часто встречаемся на древнеегипетских изображениях. Но если это и так, то почему бы посоху не быть одновременно и измерительной рейкой? Заметим, что Хасира держит этот жезл на весу, а не опирается на него, кроме того, у него нет навершия, обычного для посоха, и держит его зодчий совершенно точно посередине.
Если большой жезл равен
135-
Если действительно малый
жезл равен одному локтю (
А рост Хасира, измеренный по масштабу,
достигает
Почему же при определении размеров большого жезла понадобилось диагональ квадрата со стороной, равной локтю, удваивать? Быть может потому, что этот жезл служил одновременно и посохом или для измерения требовалась большая линейка. Возможно также, что на нем делались какие-то отметки для дополнительных делений. Сравнивая эти жезлы можно встретиться с построением ряда дополнительных соразмерностей.
Третий жезл, который держит Хасира в правой руке, своеобразной формы, он имеет какое-то ритуальное значение. Таким жезлом знатные египтяне снабжаются весьма часто. Но все же необходимо проверить, быть может, он имеет размеры, согласованные с двумя первыми жезлами?
И в самом деле, этот жезл
(fg) соотносится с половиной большого жезла (cd) как сторона
квадрата с диагональю его половины (1,12 v т. н. "функция золотого
сечения" 
). Тем самым ритуальный жезл (fg) в
сумме с длиной большого жезла относится к своей удвоенной длине в отношении
золотого сечения - 
Этот жезл членится на рукоятку и наконечник так, что его рукоятка и весь жезл соотносятся как сторона квадрата и его диагональ.
Соотношение размеров всех трех жезлов дают богатую гамму отношений, позволяющих строить самые прихотливые пропорциональные формы. Как именно использовались эти жезлы зодчим, в какой степени они универсальны, мы еще не знаем, но так или иначе, все эти пропорции часто встречаются при анализе архитектурной формы сооружений Древнего Египта и не могут быть случайными. Это обязывает нас сделать соответствующие выводы.
Теперь обратим внимание
на то, как держит жезлы Хасира. Большой жезл и жезл с наконечником расположены
на рельефе под прямым углом. Причем указывает он на точку j большого
жезла и определяет своим положением два смежные египетские треугольника с
целочисленными сторонами 3, 4 и 5. Вершина острых смежных углов этих
треугольников 
определена контуром окружности с диаметром
равным и совмещенным с большим жезлом. Эти смежные углы в cумме равны прямому
углу большого также целочисленного треугольника 
, вписанного в
полуокружность с диаметром, равным большому жезлу. Эти построения настолько
наглядны, что не вызывают никаких сомнений в их подлинности.
Очевидно желание художника показать на рельефе соотношения, осуществляемые при помощи всех трех жезлов. Как мы уже говорили, они дают примеры построения отношений: стороны и диагонали квадрата, "двойного золота", функции золотого сечения и целочисленного египетского треугольника. Приходится удивляться столь тщательной разработке египетскими зодчими подобных пропорциональных соответствий.
Обратимся теперь к
композиционным закономерностям этого замечательного рельефа в целом. Нетрудно
заметить, что размещенная над рельефом иероглифическая надпись с титулатурой
зодчего имеет прямоугольную рамку со сторонами, соотносящимися как катеты
египетского треугольника, т.е. 
, причем размеры этой
рамки прямо повторяют катеты большого египетского треугольника 
, о
котором мы только что говорили. Как следствие большой жезл оказался равен
диагонали рамки надписи 
.
Изображение самого Хасира
разместилось на доске прямоугольной формы в рамке, имеющей соотношение сторон, равное
золотому сечению 
. Меньшая сторона этой рамки приравнена
большой стороне обрамления надписи.
Чуть отклоняющийся от горизонтального
положения жезл с наконечником: если продолжить его ось до пересечения с
границами изображения, то эти границы окажутся почлененными v левая в отношении
, а правая v в отношении золотого сечения.
Если таким же образом продолжить ось большого жезла до пересечения с верхней и
нижней границами изображения, занятого фигурой Хасира, то нижняя граница будет
почленена в отношении 1 к 2, а верхняя v в пропорции "двойного
золота", близкого по значению отношению 
.
Продолженная до пересечения с рамкой изображения ось малого жезла вверху придется на угол, а нижнюю границу членит в отношении функции золотого сечения.
Сделаем теперь попытку проследить построение пропорций изображения фигуры самого Хасира (схема соразмерностей 2).
Высота изображения Хасира
до плеч (места срастания ключиц) оказывается равной трем локтям 
, или
трем малым жезлам. Первое членение приходится на колени, второе v на талию,
определенную поясом юбочки, и третье v на уровень плеч, оно же определяет
величину шага. Опущенная рука приходится на середину высоты фигуры, также не
считая голову. Четвертая часть определяет ширину плеч и сгиб руки в локте, тот
же размер определяет и шаг, измеряемый от пяты до пяты. Талия равна половине
ширины плеч. Высота головы приравнена 1/5 высоты фигуры
до плеч. Длина ступни также равна 1/5 высоты. Таким образом,
узловые членения фигуры человека определяются при помощи наложенных друг на
друга членений его высоты на 3, 4 и 5.
Общий контур фигуры легко определяется двумя симметричными равнобедренными треугольниками с общей вершиной, имеющими каждый высоту в два раза большую, чем основание. Основание же равно ширине плеч и шагу, измеренному "в свету", это четверть высоты фигуры. Высота фигуры (не считая головы) определяется равнобедренным треугольником, имеющим высоту в три раза большую, чем основание, равное шагу Хасира, измеренному по наружному контуру.
Знакомясь с альбомом Гоннекура, мы видели начертания, подобные установленным нами. Однако почему Гоннекур называет такую схему "романским каноном" (или римским?), остается неясным.
Эта геометрическая схема, определяющая абрис фигуры, в более поздних изображениях Древнего Египта усложняется. Так, в нарушение симметрии шаг замеряется уже от пяты до пяты, а не в просвет шагающей фигуры, как у Хасира, и пр. Материала для аналитических исследований содержится в египетских рельефах предостаточно и надо надеяться, они послужат благодатной темой для будущих исследований.
Во всей истории искусств мы не встречаем ничего подобного египетским рельефам. Наиболее близкие им рельефы Ассирии, приобретая новые качества, теряют ту точность и многообразие информации, которыми они отличались.
Предложенный анализ рельефного изображения Хасира v древнеегипетского зодчегоvвельможи Древнего царства (III тысячелетие до н. э.), приводит к важному заключению. Каждый жест зодчего, находящиеся в его руках инструменты, пропорции фигуры, композиция самого изображения - все определяется расчетом или геометрическим построением. Перед нами не рисунок или рельеф в современном понимании, а своего рода чертеж. Математические соразмерности вооружают художника в его труде, являются своего рода «формой» его художественной интуиции.
Самый скрупулезный анализ одного, даже пусть замечательного произведения искусства, не может дать исчерпывающих данных и установить характерные черты рабочего метода художника. Над изучением древнеегипетского рельефа, как мы уже отметили, его "информативности" и закономерности художественной формы и композиции придется еще очень много потрудиться.
Для подтверждения достоверности выводов проведенного исследования и нашего права использовать при анализе всю сумму геометрических построений вплоть до золотого сечения, мы приведем дополнительно некоторые, на наш взгляд, убедительные свидетельства.
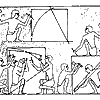
Так, напомним о другом египетском
рельефе(5), также относящемуся к Древнему Царству (2800-
Один из каменщиков
обрабатывает блок, имеющий соотношение сторон, равное отношению стороны
квадрата к диагонали его половины 
. Это отношение - так
называемая функция золотого сечения (термин, предложенный И. В. Жолтовским). С
помощью той же диагонали, но повернутой около другого своего конца, мы можем
построить прямоугольник в пропорции золотого сечения.
Второй блок камня
обрабатывают три каменщика, этот блок имеет соотношение сторон . Это
соотношение получило очень широкое распространение в искусстве. Во-первых, оно
легко образуется из египетского треугольника. Во-вторых, оно весьма близко к
"двойному золоту", т. к. отношение двух меньших отрезков пропорции
золотого сечения относятся к одному большему отрезку как 
,
т.е. весьма близко к отношению 
. В-третьих, отношение 
весьма близко к отношению граней кубов, из
которых один вдвое по объему превышает другой - 
. (Заметим, что
такое изысканное произведение как «Троица» А. Рублева написано на доске,
имеющей именно такое соотношение сторон v )
Третий блок имеет соотношение
сторон равным 
, что соответствует катетам целочисленного
треугольника 20, 21, 29. То, что в данном случае имеется в виду именно такой
треугольник, демонстрируется одним из каменщиков, измеряющим диагональ блока,
которая в этом случае должна быть равной 29.
Таким образом, одно это
изображение убедительно свидетельствует об осведомленности древнеегипетских
зодчих, а, следовательно, скульпторов и художников о соотношениях египетского и
других целочисленных треугольников, об отношении "функции" и золотого
сечения, а также значении такого соотношения как . Все это
указывает на достоверность проведенного нами анализа изображения Хасира с
использованием всей суммы упомянутых отношений.
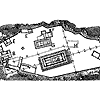
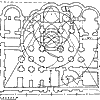
И, наконец, для полной убедительности и понимания необычайной роли и значения, которое имели математические характеристики художественной формы в древнеегипетском искусстве, напомним о пропорциональности пирамид Хеопса, Хефрена и Микерина, образующих ансамбль в Гизе (илл. 2 ).
Нет сомнений в том, что, предпринимая строительство таких гигантов, зодчие очень и очень внимательно рассчитывали все их размеры. Иначе невозможно мыслить организацию этого чрезвычайного по масштабам строительства. Точные соразмерности этих сооружений не вызывают ни малейших сомнений. Однако, анализируя форму пирамид, мы встречаемся с некоторыми трудностями. Дело в том, что пирамиды потеряли свой облицовочный слой и их точный первоначальный размер остается на совести обмеряющих и реконструирующих их форму исследователей. В литературе встречаются обмерные данные, несколько отличающиеся друг от друга(7). Строительство, вероятно, велось вначале без лицевого слоя, так как иначе свести все четыре грани в одну точку v вершину пирамиды было бы невозможно. Облицовку проводили, начиная с верха, что и обеспечивало точность и остроту формы. Впоследствии за многовековую историю, облицовочный слой был почти полностью утрачен.
Пирамида Хеопса имеет
стороны основания: 230,41, 230,51, 230,60 и 
(8) . Анализ
пропорций пирамиды Хеопса не оставляет и тени сомнения в том, что зодчие
древнего Египта превосходно знали и высоко ценили отношение золотого сечения.
Пирамида Хефрена
построена на основе отношений сторон священного египетского треугольника. Ее
поперечный разрез определяется двумя треугольниками, сблокированными своими
большими катетами. Проверим. Сторона основания равна 
.
Обмерные данные,
приведенные в ВИА(9), несколько иные, по-видимому, определены в другом уровне,
но они дают тот же результат: 
. Архитектурные формы
пирамиды Хефрена как нельзя лучше свидетельствуют об использовании зодчими
Египта целочисленного треугольника 3, 4, 5.
Пирамида Микерина имеет
сторону основания 
. И в этом случае мы имеем вполне
устраивающие нас результаты, так как отклонение от абсолютно точного
соотношения незначительно и может быть отнесено на счет неточных обмеров
памятника и реконструкции облицовочного слоя, а равно и ошибок в строительстве.
Итак, анализ архитектурной формы пирамид ансамбля в Гизе неопровержимо свидетельствует о том большом значении, которое имели для построения архитектурной формы еще в Древнем Египте, за З000 лет до нашей эры, целочисленный египетский треугольник, недаром называемый священным, и отношение золотого сечения, получившее также в последствии название дивной, божественной пропорции.
Парфенон и Эрехтейон. Античный ордер и канон Поликлета
Внимание историков
античной архитектуры прежде всего сосредоточивается на памятниках афинского
Акрополя. В
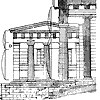
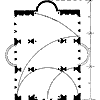
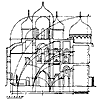
Храм сооружен из пентелийского белого мрамора, со временем приобретшего теплый желтоватый цвет (илл. 3). Мраморные блоки укладывались насухо и соединялись металлическими вкладышами. Даже кровля покрывалась мраморными пятисантиметровыми плитами - "черепицей". Храм относится к числу широко распространенных периптериальных античных храмов, отличие его заключается в пропорциональном гармоническом строе.
?Биография» Парфенона
полна самых подчас драматических событий. Около девяти веков существовал храм
Афины Парфенос, но вслед за торжеством христианской религии - этой важнейшей
гранью человеческой истории - Парфенон становится храмом Богородицы. В
Эрехтейоне и Пропилеях также располагаются христианские церкви. В годы
Латинской империи (1204-
Эпоха Ренессанса в Европе
XV-XVI веков не знала античной греческой культуры. Памятники Акрополя оставались
в неизвестности. Лишь с XVII века посетители Афин делятся своим восторгом от
красоты хорошо еще сохранившихся памятников архитектуры Акрополя. Орден
капуцинов составляет первый план Афин и Акрополя (
С XVIII века возрастает
внимание к античному искусству. Винкельман пишет свой знаменитый труд «Историю
искусства древности». В
Многое следовало бы рассказать об этом исключительных достоинств храме, но в данном случае речь идет преимущественно о его гармоническом « пропорциональном строе. Опубликовано много вариантов пропорционального анализа Парфенона. И мы, в свою очередь, имеем в виду предложить свой вариант системы пропорций, которая, как нам кажется, приближает к пониманию метода гармонизации архитектурной формы античными зодчими. Конечно, мы далеки от мысли буквально воспроизвести во всех деталях метод творческого труда зодчего и ограничимся лишь тем, что все наши ухищрения не будут нарушать круга возможных знаний античных мастеров архитектуры и не выйдут за пределы античной науки.
Необходимо так же отметить, что указанные ниже пропорциональные закономерности, если не все, то многие из них, ранее были уже установлены другими исследователями, мы же сосредоточим усилия на рассмотрении последовательной цепи пропорциональных построений, обеспечивающей формальное гармоничное совершенство столь значительного для художественной культуры человечества памятника архитектуры, каким является Парфенон. Приступая к пропорциональному анализу Парфенона, следует иметь в виду, что обмеры храма, которые были сделаны многими авторами, а, следовательно, и опубликованные чертежи, иногда заметно отличаются друг от друга. А это значит, что и пропорциональные отношения, отмечаемые нами, не могут быть совершенно точными. Кроме того, и при возведении памятника неизбежны хотя бы незначительные погрешности. Своеобразие архитектурной формы Парфенона заключается в наличии курватуры, которая служит оптическим коррективам, обеспечивающим правильное видение архитектурной формы. Стилобат храма не строго горизонтален, а слегка выпуклый, колонны разного диаметра и пр. Храм по идее прямолинеен, на самом же деле в его контурах нет почти ни одной строго прямой линии. Процесс проектирования, очевидно, заключался в гармонически рассчитанной форме, которая вслед за тем корректировалась по законам курватуры, или восприятия. Именно поэтому мы можем встретиться при анализе с некоторыми не только вызванными случайными обстоятельствами, но и предусмотренными зодчим в процессе проектирования отклонениями от расчетной нормы. Некоторые деформации памятника могут быть отнесены на счет времени, землетрясений и, наконец, взрыва.
Характер производства работ и строительного материала требовал в работе предельной точности. Каждый отдельный блок мрамора обрабатывался отдельно по установленным зодчим размерам. Если в таких условиях не быть абсолютно точным, то камень не ляжет на свое место, что и обусловливает в античной архитектуре точное соблюдение всех соразмерностей. Данные нашего анализа основываются на прекрасно выполненных чертежах увража M. Collignon(10), содержащего обмерные данные и сопровождающий текст. Проверка геометрических закономерностей обмерными данными при наличии достаточно крупных и точных чертежей вряд ли должна быть признана обязательной. Погрешности в построении будут заметны и на чертеже, но все же для суждения о точности построения соразмерностей мы будем проверять предлагаемые геометрические по своей природе закономерности не только чертежом, но и данными натурных обмеров.
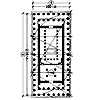
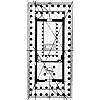
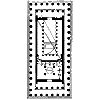
Стилобат Парфенона,
измеренный по верхней кромке, имеет меньшие стороны (восточного и западного
фасадов), равные по обмеру
Мы не склонны видеть в 100-футовом стилобате модуль в современном понимании этого термина. Это тот размер, с которого начинается проектирование, тот размер, который служит заданием для зодчего, тот размер, который устанавливается, быть может, по совету зодчего заказчиком. Используя музыкальный термин, мы в данном случае говорим о "тонике". Главный восточный фасад - ширина храма подобна, по Витрувию, расстоянию между уключинами корабля, в соответствии с которым определяются все его соразмерности... Витрувий упоминает в качестве модульного размера диаметр колонн. И действительно, диаметр колонны имеет значение как мера, используемая для определения соразмерностей ордера. Это модуль чисто ремесленный и определяется зодчим, исходя из размеров ордера. Понятно, что размеры всего здания, его величина, определяются заказчиком, а диаметр колонн устанавливается по законам гармонии зодчим и только самим зодчим.
В качестве примера можно привести соразмерности в плане античного жилого дома. Модулем соразмерности явился размер ложа для человека; или, что то же у японского жилого дома: соразмерности плана устанавливаются размерами циновки. Этими "функциональными" нормативами руководствуются зодчие в процессе проектирования или строительства. Заметим кстати, что в современном проектировании архитектор в своем творчестве буквально задавлен множеством нормативов, не оставляющих для него возможности точно соизмерять форму сооружения. Проектирование ведется при наличии большого числа плохо согласующихся друг с другом «размеров, принятых за исходные» (по Витрувию).
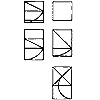
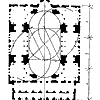
Соотношение меньшей
стороны стилобата храма и его большей стороны приравнено отношению стороны
квадрата и удвоенной диагонали его половины 
. Отношение стороны квадрата к
диагонали его половины было названо "функцией золотого сечения" и
широко нами используется 
. Квадрат служит основанием для построения
целого ряда соразмерностей (рис. «Квадратные» соразмерности). Речь идет не
только о простейшем соотношении стороны квадрата и его диагонали 
или
ряде вписанных друг в друга квадратах, а также о построении отношения стороны
квадрата к его стороне в сумме с полудиагональю 
, и
вышеназванного соотношения функции золотого сечения - стороны квадрата и
диагонали его половины и особенно для нас важного отношения
стороны квадрата к диагонали его половины в сумме с половиной стороны исходного
квадрата, т. н. "золотого сечения" 
и производные к ним.
Все эти соотношения
легко осуществляются в натуре при помощи весьма несложных геометрических приемов
и по методам построения весьма близким друг другу. Не следует думать, что
отношение золотого сечения или &q" золотого сечения это нечто
глубокомысленное и математически сложное. Напомним, что отношением золотого
сечения называется отношение целого к большей части, равным отношению большей
части к его меньшей части. 
.
Отношение большой и малой
сторон стилобата Парфенона может быть выражено, минуя функцию золотого сечения,
непосредственно при помощи золотого сечения (схема соразмерностей 1). В самом
деле, контур стилобата может быть построен при помощи прямоугольника в
отношении золотого сечения и второго, сопряженного с ним прямоугольника
золотого сечения, имеющего большую сторону равной и совмещенной с меньшей
стороной большого прямоугольника. Нетрудно видеть, что оба приема построения
стилобата храма идентичны - 
. Или еще проще: соотношение сторон
стилобата устанавливается соотношением 
. По обмеру меньшая
сторона стилобата равна 30,89. Вычисляя большую сторону в соответствии с
установленными соотношениями, получим 
. По обмеру тот же размер
равен 69,50. Расхождение между теоретическим размером и обмерными данными равно
Заметим, что строители Парфенона Иктин и Калликрит в данном случае не проявили особой изобретательности, например, храм Геры в Пестуме (или т. н. базилика, относящаяся еще к VI в. до н. э.), имеет то же соотношение сторон, измеренных по кромке стилобата, что и Парфенон; у храма Зевса в Олимпии (ок. V в. до н. э.) мы вновь встречаем все то же отношение. Здесь же заметим, что установление границ архаического и классического периодов в истории искусств античной Греции для развития архитектурных форм вряд ли имеет серьезное обоснование.
Однако следует обратить
внимание на то, что длина сторон у Парфенона совершенно точно соответствует
отношению простых чисел 
. 
(расхождение в 
, а практически оказалось
удобнее оперировать для расчетов и строительства отношением 
или 
. Тем более что в Древней Греции рассчитать
точно отношение иррационального по своей природе размера, такого, например, как
сторона квадрата и диагональ его половины, было затруднительно, а соотношение для них было достаточно точным решением
этой задачи.
В такого рода постановке вопроса можно видеть характеристику древнегреческой прикладной математики или, по крайней мере, расчетных методов, к которым прибегали древнегреческие зодчие, устанавливающие соразмерности своих сооружений. Конечно, единичный пример не может служить достаточно серьезным основанием для далеко ведущих выводов, но в данном случае пример уж очень весомый.
Установив ширину и длину храма, мы могли бы обратиться к определению его высоты, но прежде все же мы выясним основные соразмерности сооружения в плане.
Ширина целлы, измеренная
по наружным стенам, соотносится с уже установленной нами длиной храма в
отношении меньшего и удвоенного большого отрезка золотого сечения (схема
соразмерностей 2). Соотношение выдержано весьма точно 
, по обмеру же
ширина целлы равна
Cтороны целлы, измеренные
по наружным стенам без портиков, соотносятся, как и стороны стилобата, т. е.
меньшая сторона - ширина целлы относится к большей стороне как меньший отрезок
относится к удвоенному большему отрезку функции золотого сечения 
. Это
отношение определяет одновременно глубину портика. Это весьма точно
установленное соотношение не может быть заменено отношением , как
это было сделано при определении размеров стилобата, что и свидетельствует
лишний раз о преимущественном внимании к иррациональным построениям, когда
соотношение устанавливается в относительно меньшем размере.
Глубины внешнего и внутреннего портиков восточного и западного фасадов храма равны друг другу.
Портики восточного и западного фасадов храма по глубине приравнены половине ширины целлы, измеренной по наружным стенам. Указанная соразмерность получается сама собой как следствие предшествующих построений. Интересно и здесь отметить, что соразмерности или пропорции, заложенные в построении, как бы множатся, продолжая одни других.
Диаметр колонн относится к глубине внешнего портика восточного и западного фасадов храма в золотом сечении.
Диаметр основания колонн внутреннего портика относится к его глубине как один к двум.
Ступенька стилобата выступает за его верхнюю кромку на меньший отрезок золотого сечения, если больший отрезок приравнен основанию колонн.
Стена целлы со стороны входа (с востока и запада) приравнена по толщине диаметру колонн, 3аметим, что толщина стены в этом случае "видна" человеку, входящему внутрь храма.
Ширина целлы, измеренная
в интерьере, соотносится с полной шириной храма в золотом сечении: 
, по обмеру - 19,18.
Продольный размер целлы в интерьере (в сумме с опистодомом) относится к полной длине храма также в золотом сечении. Иначе говоря, поперечный размер целлы и ее продольный размер соотносятся так же, как стороны храма, измеренные по кромке стилобата (см. выше) и повторяют отношение длины и ширины целлы, измеренные извне по стенам, что оказалось возможным благодаря разным толщинам ее продольных и торцевых стен.
Поперечная стена, разделяющая наос и опистодом, членит храм по оси на две части в золотом сечении (схема соразмерностей 3). При этом продольный размер опистодома приравнен большему отрезку золотого сечения по отношению к половине общей длины целлы.
Опистодом имеет соотношение сторон
равное 
(с небольшим приближением).
Центральный неф наоса равен половине его полной ширины или 1/3 его длины (измерение ведется по основанию колонн).
Глубина нефа в пределах колоннады приравнена стороне квадрата, равной ширине нефа в сумме с большим отрезком золотого сечения, если меньшим отрезком будет сторона того же квадрата.
Высота ордера и, что то же самое,
высота храма так относится к ширине главного фасада, равной 100 греч. футам,
как та же ширина фасада относится к длине храма (см. след. рис.). Соотношение
высоты ордера и ширины храма равно , и в этом случае высота
ордера равна 
м. По обмеру она равна
Если полную высоту ордера поделить в
отношении золотого сечения и вслед за тем меньший отрезок вновь поделить в
отношении золотого сечения, то больший отрезок в повторном членении определит
размеры антаблемента. По расчету высота антаблемента равна: 
; 
, по обмеру же - 
, а вслед за тем 2 поделить, в свою
очередь, на 5, то три части из пяти определят антаблемент 
м.
Очевидно, что зодчий и в этом случае предпочел дело иметь с целочисленными
величинами очень близких к значению иррациональных построений. Точка в нашем
построении находится в верхней части колонны на высоте
Антаблемент Парфенона членится на
архитрав (1,34), фриз(1,34) и карниз (0,61). Карнизный камень равен по толщине
меньшему отрезку, если архитрав (или фриз) разделить в пропорции "двойного
золота" или 4 : 5 
см, по обмеру также 
или к архитраву, равному фризу, как .
Имея в виду принципиально важный вопрос теории пропорционирования, заключающийся в характеристике малой по размеру и крупной архитектурной формы, обратимся к сравнению дорического ордера Парфенона и дорического ордера Пропилей афинского Акрополя. У ребенка голова относительно его роста велика, у взрослого человека - значительно меньше. Исходя из этого тезиса, мы ожидаем каких-то изменений в пропорциях крупного ордера Парфенона и ордеров Пропилеев меньшего размера.
Большой ордер Пропилей имеет высоту
равную 
.
Малый дорический ордер Пропилей имеет
высоту, равную .
Но что для нас является совершенно неожиданным, так это тождественность пропорции всех трех дорических ордеров, несмотря на столь значительные различия в их абсолютных размерах. (Кстати, заметим, что детей греки изображали в пропорциях, близких к взрослым).
Размеры антаблемента по отношению к величине ордера у Парфенона (см. выше) соотносятся как большой отрезок золотого сечения, членящего меньший отрезок золотого сечения от общей величины ордера. Совершенно то же соотношение размеров антаблемента и высоты ордера мы встречаем как у большого, так и малого ордеров Пропилей.
Расстояние между колоннами у Парфенона (в рядовом случае) устанавливается в отношении к диаметру колонны в пропорции "двойного золота". С тем же отношением мы встречаемся у большого и малого ордеров Пропилей.
Фриз и архитрав антаблемента Парфенона равны по высоте. С тем же отношением мы встречаемся в обоих ордерах Пропилей.
"Вертикальный" размер
карниза у Парфенона равен меньшему отрезку пропорции "двойного
золота" 
по отношению к размерам фриза или равного
ему архитрава. А у дорических колоннад Пропилей карнизное венчание антаблемента
приравнено меньшему отрезку золотого сечения по отношению к размерам фриза, в
чем и заключается единственное различие в пропорциях этих ордеров.
Приведенные данные свидетельствуют, что греческие зодчие классического периода V в. до н. э. не ставили в прямую связь пропорции дорического ордера от его абсолютных размеров. Вывод, прямо надо сказать, неожиданный. И все же было бы очень интересно и важно проследить композиционную связь масштабности сооружения и его пропорциональности не на одном - двух примерах, а с более солидным обоснованием.
Следует напомнить, что отношение
"двойного золота" равно 0,806, что весьма близко отношению 
. Попутно вспомним, что отношение ребер
куба и куба удвоенного объема так же весьма близко отношению и
равно 0,79З. Все это требует, как мы уже говорили выше, особого внимания к
отношению , которое имеет как бы тройной
"коэффициент полезного действия".
Отношение ордеров, а, следовательно,
и колонн Парфенона и восточного портика Пропилей по высоте ближе всего к
отношению двойного золота. Тем самым любопытно отметить, что отношение объемов
колонн Парфенона и восточного портика Пропилей устанавливается отношением 
(13) . Вообще говоря, соотношение объемных
тел установить очень непросто, но в данном случае при строгой идентичности
пропорций колонн и при отношении их линейных размеров близком к 0,79, задача
решается вполне удовлетворительно. Такого рода наблюдение особенно интересно,
так как пропорциональный строй античной архитектуры не мог, на наш взгляд,
игнорировать проблему пропорционирования объемов.
Можно думать, что совершенство древнегреческой скульптуры сознательно или инстинктивно основывается на гармонии объемов, и рано или поздно мы должны будем заняться вплотную исследованием этого вопроса, не удовлетворяясь проблемой удвоения куба.
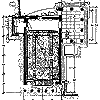
Эрехтейон - храм на афинском
Акрополе сооружен в 421-
Храм сооружен в ионическом стиле.
Композиционная сложность Эрехтейона в данном случае не является предметом наших суждений. Заметим лишь, что зодчий, сооружавший в конце V в. этот необычайный храм, сумел наилучшим образом активно войти в ансамбль Акрополя и, прежде всего, сопоставить его с архитектурой Парфенона. Ансамбль в этом случае строится на принципе гармонического контраста, но не контраста противоречия. Соседство с Эрехтейоном обогащает архитектуру Парфенона. Его строгая, простая и величественная архитектура находит в Эрехтейоне своего рода "отдых" - развлекая человека, быть может, "утомленного" этим величием. Приближаясь к "человеческому" масштабу, Эрехтейон становится как бы ближе по своей архитектуре к жилищу человека, а не дому богов-героев.
Анализ соразмерностей Эрехтейона весьма сложен. Чтобы до конца разобраться во всех деталях построения его архитектурной формы, необходимо затратить очень много сил, внимания и времени. Подробный анализ дал бы полную картину изысканного мастерства древнегреческого зодчества и гармонических основ искусства классической Греции.
В данном случае мы ограничиваемся лишь анализом структурных элементов храма и соразмерностей его ордера.
Прежде чем обратиться к изучению пропорций ионического ордера портиков Эрехтейона, мы должны установить их общий размер, а потому обратить внимание на размеры и соразмерности плана этого удивительного сооружения.
Основной объем храма с портиком ориентирован по традиции на восток. Западный портик оказался высоко поднятым и обеспечивает освещение перегороженного поперечной стеной интерьера храма. Большой глубокий просторный северный портик с входом, обрамленным замечательным наличником, делает этот вход в храм если не главным, то равнозначным входу восточного портика. Назначение портика Кариатид остается неясным. Быть может, он служил своего рода трибуной при проведении каких-то религиозных или общественных празднеств.
Ширина основного объема храма
равна
У Эрехтейона, как и у старого храма
Афины, соотношение ширины и длины равно 
; 
м; по
обмеру так же точно - 22,32.
Северный портик выступает за пределы
западной стены храма на размер, определяемый диагональю основного объема храма.
Причем полная длина храма, считая выступающую часть северного портика,
соотносится с шириной храма как 
, т.е. в пропорции плана
Парфенона. 
; по обмеру - 
. Однако
необходимо обратить внимание, что 
. Иначе говоря,
соотношение сторон двух функциональных "квадратов" 
устанавливается
также, как и у Парфенона: упрощенным соотношением (
).
Иначе говоря, портик выступает на 1/4 часть ширины храма.
Если южную стену храма по длине
разделить на равные четыре части, то мы получим продольный размер портика
Кариатид. 
, по обмеру также 5,58.
Портик Кариатид выступает от южной
стены храма по отношению к его продольному размеру в отношении 
.
Изнутри в плане он имеет соотношение сторон 
- соотношение выдержано
точно.
Положение западной грани северного
портика определено выше. Восточная грань его определяется 1/3 длины
северного фасада храма. Глубина портика, измеренная по кромке стилобата до ант,
относится к его ширине в золотом сечении. Ширина и длина северного портика за
колоннами соотносится как . Это соотношение повторяет принцип
построения портика Кариатид.
Эрехтейон расположен на рельефе. По высоте западного и северного фасадов его высота оказалась приравненной ширине, иначе говоря, основной объем храма представляется как бы составленным из двух кубов.
Определив основные соразмерности храма в плане, обратимся к определению высоты каждого из четырех ордеров Эрехтейона . Величина ордера естественно устанавливается из размеров самого сооружения и является прямым следствием размеров храма.
Высота храма, а также ордера
восточного портика в сумме с меньшей долей золотого сечения от его высоты
приравнена ширине портика (или всего храма): 
, по обмеру -
Антаблемент приравнен половине малого
отрезка золотого сечения всей высоты ордера: 
м, по обмеру то же -1,53.
Диаметр колонны под капителью равен
архитраву -
Высота колонны восточного портика
Эрехтейона соотносится с высотой колонн Парфенона в золотом сечении или,
точнее, как - 
.
Высота колонн восточного портика
Эрехтейона относится к колоннам Пропилей как - 
.
Все четыре ордера Эрехтейона имеют прямую пропорциональную взаимозависимость.
Обращает на себя внимание
сопоставление пропорций, основанных на иррациональном отношении золотого
сечения и простейших однозначных цифр. Так, северный портик и портик Кариатид
изнутри в плане в интерьере определяются отношением , а извне
пропорцией золотого сечения.
Ордер северного портика имеет соотношения, установленные, как и у других ордеров, отношениями золотого сечения и в то же время с добавкой по высоте симы характеризуется простейшими цифрами. Однако такие сопоставления еще не получили своего убедительного истолкования, но очевидно, что противопоставление этих методов не обосновано, необходимо искать их взаимопроникновение.
Мы не будем загромождать повествование излишними подробностями. Детальный анализ пропорций Парфенона и Эрехтейона - дело чрезвычайно интересное и имеющее большое значение для истории искусства античности, но в данном случае перед нами стоят ограниченные цели: провести сравнение между античным ордером и каноном человеческого тела, установленным древнегреческой скульптурой. Это сравнение уже давно "на языке" искусствоведения и истории архитектуры, но нам этого мало, это сравнение необходимо провести на базе точного анализа, аргументированного геометрией.
Наилучшим примером для анализа пропорций идеального человеческого тела, установленных античными греческими скульпторами, мы избираем, прежде всего, Дорифора работы Поликлета. Это тем более основательно, что именно этой скульптуре было присвоено наименование "Канон".
Длина ног Дорифора равна половине его роста.
Поделив высоту Дорифора в отношении , определяем положение пупка.
Поделим верхний отрезок, в свою очередь, на 3 равные части: одна часть определит размер головы.
Половина верхнего отрезка определит голову и шею до плечевого пояса или ключиц.
Наша задача заключается также в определении пропорций человека, которые откорректированы Праксителем в IV в. до н. э., и сопоставить их, если это окажется возможным, с пропорциональным построением архитектурных ордеров.
Длина ног у Гермеса работы Праксителя равна половине роста человека
Разделив рост человека в пропорции золотого сечения, установим положение пупка.
Разделив верхний меньший отрезок золотого сечения пополам, устанавливаем основание шеи (ключицы, как указано выше).
Если разделить тот же меньший отрезок золотого сечения в свою очередь в золотом сечении, то размер головы будет определен его меньшим отрезком.
Если нижний больший отрезок золотого сечения от высоты человека разделить в золотом сечении, то обозначится положение колен.
Если же нижнюю половину от высоты человека поделить пополам, то также определится положение колен.
Длина рук приравнена половине высоты человека без учета головы.
Плечи, измеренные по плечевым суставам, могут быть приравнены голове и шее или половине меньшего отрезка золотого сечения от роста человека.
Античный канон человеческой фигуры интересно проследить в его становлении и развитии. Анализ пропорций скульптур VI в. до н. э. - Кор и Куросов дает примеры использования тех же пропорций, что и в V в. Некоторые изменения канона мы встречаем уже в IV в. и в эпоху эллинизма. Тема эта может быть положена в основу специального детального исследования.
Проведенный анализ пропорций античных скульптур человеческой фигуры основан на золотом сечении, это отнюдь не противоречит свидетельству древних авторов - Плиния, Варрона, которые говорили о "квадратных" скульптурах Поликлета. Напомним, что простейший метод построения пропорции золотого сечения основан на элементарных геометрических построениях квадрата и его диагоналей. Было бы неосновательно ограничивать "квадратные" построения только диагональю и стороной квадрата.
Для наших целей данных проведенного анализа вполне достаточно. У нас есть веское основание говорить об аналогии в приемах построения античными архитекторами и скульпторами пропорций ордера и скульптуры человека. Уже в архаическую эпоху в Греции установлена система ордеров в архитектуре и были установлены пропорции человеческого тела, что мы видим на примере Кор и Куросов. Изысканная и пластически совершенная скульптура и архитектура классики V в. не опрокинула системы пропорциональности архаики, а ее усовершенствовала.
При сравнении приемов построения
пропорций ордера и скульптуры человека очевидным кажется полное совпадение
методов. У дорического ордера, почлененного в отношении , меньший отрезок,
поделенный в свою очередь в той же пропорции, устанавливает размеры
антаблемента, подобным же образом определяется у скульптуры размер головы.
Равно как у ионического ордера, так и в скульптуре Праксителя, почлененных в
золотом сечении, верхняя меньшая часть, поделенная пополам, определяет
антаблемент ордера и голову человека с шеей до плечевого пояса. И тут и там
устанавливаются несущие и несомые элементы фигуры и ордера.
Аналогия в построении пропорций ордера и человека не является чем-то неожиданным. Более того, она предсказывалась в самых общих суждениях, содержащихся у разных авторов. Особенно ярко о скульптурной пластике античной архитектуры говорит Н. И. Брунов(16). Мы же в данном случае стремились к конкретизации этой идеи в соразмерностях и пропорциях.
В отличие от суждений Н. И. Брунова, наш пропорциональный анализ говорит не о колонне, а о полном ордере как аналоге человека, причем антаблемент, а не капитель является его "головой". При этом указание на кариатиды, как бы заменяющие колонны, должно быть откорректировано; они "вставляются" в ордер, заменяя лишь части колонны без антаблемента, капители и базы. Они лишь сопоставляются в общем виде с идеей ордера и человека.
От Парфенона до Софии Киева и Новгорода
Парфенон
"Гекатонпедос. Храм
на Акрополе в честь Девы (Парфенон), построенный афинянами (447-
"Гекатомпедон. Храм Афины, сторона которого равна ста греческим футам. Потому-то он и был назван так. Некоторые называют его Парфеноном (Большая Этимология)"(17). В противоречие с этим во Всеобщей истории архитектуры (гл. II, кн. 2) Гекатомпедоном назван старый храм, на фундаментах которого частично расположился Эрехтейон. Но не в этом суть дела, в данном случае нас интересует лишь то, что у Парфенона, как мы уже установили ранее, главные торцевые фасады по ширине, измеренные по кромке стилобата, равны 100 греч. футам (г. ф.).
Если верить справочникам,
г. ф. равен
Последующая судьба этих ста г. ф. удивительна. Сто г. ф. мы встречаем в качестве исходного размера, использованного для построения плана ряда значительных сооружений, начиная с V в. до н. э. вплоть до XIII в. н. э. - по крайней мере, на протяжении восемнадцати веков! Это ли не удивительно. Проследить эту своеобразную "эстафету" и является одной из наших задач.
Итак. О пропорциях
Парфенона мы достаточно подробно говорили в предыдущем очерке. Здесь же
повторим, что отношение сторон храма, измеренных по кромке стилобата, устанавливается
квадратом и двумя прямоугольниками золотого сечения с большей стороной, равной
стороне исходного квадрата. (Варианты построения контура Парфенона в плане см.
в предыдущем очерке) Построение выполнено довольно точно. Ошибка не превышает 1/3
процента длины храма. Однако соотношение сторон храма приравненное еще точнее соответствует обмерным данным.
Но "исходный размер", приравненный
Попытки объяснить, почему
храму приданы именно такие, а не какие-либо иные размеры, могут быть сделаны в
связи с анализом архитектурного ансамбля и размерами самой скалы Афинского
Акрополя. В самом деле, ширина Акрополя по линии восточного главного фасада
Парфенона равна
Соизмеримость храма и всего холма Акрополя предопределяет его стофутовый размер и характеризует принципы формирования древнегреческими зодчими архитектурного ансамбля.
Сто футов как некий
типовой размер встречались в греческой архитектуре, по-видимому, и раньше. Так,
храм Зевса Олимпийского имеет по длине около
Грандиозный купольный храм с обширным портиком хорошо сохранился до наших дней. Он расположен на небольшой площади современного Рима, затесненной улочками и переулками. Жилые дома, измельченные множеством окон и промежуточных карнизиков, контрастируют с крупными архитектурными формами Пантеона. Кажется, что храм сооружен для высших целей и не имеет отношения к повседневным заботам человека. Окон у храма нет, освещается он круглым отверстием, обращенным в небо, расположившимся в центре купола. Однако интерьер храма не следует сравнивать с каким-то гротом или пещерой. Совсем нет, отверстие вверху как бы сближает его с небосводом, придает ему "космический характер". Большой глубокий 16-колонный портик отчуждает храм от окружающего его пространства и в то же время служит промежуточным звеном между интерьером храма и внешним миром.
Идея произведения -
замысел зодчего, архитектурно-образный строй храма заключается в его куполе,
имеющем диаметр, равный
Купол Пантеона - это дерзновенная инженерная конструкция и одновременно чистая, классически ясная архитектурная форма. Опрокинутая над вами гигантская полусферическая каменная чаша, материальность которой подчеркнута кессонами, вначале не кажется столь большой. Она имеет героический, преувеличенный масштаб и заставляет человека представлять себя в соответствии с куполом героем или олимпийцем. Это даже не героический, а божественный масштаб, как и должно быть у храма - обиталища всех богов.
Размер вещей постигается сравнением с ростом человека, недаром меры длины определяются его членами: пядь, фут, шаг, палец... Но если пирамиды Египта или Пантеон Рима представить себе в пустыне, где не с чем их сравнитъ, то что нам определит их размеры? С жилищем, даже покинутым людьми, все ясно, о масштабе человека нам расскажут двери, окна, скамья, печь, а о сооружении для богов - каков Пантеон Рима. О виадуках, о крепостных стенах и иных инженерных сооружениях, их масштабности мы судим не по росту человека, а по человеческим трудам, возможностям организации строительства, и главным критерием архитектурного масштаба являются оптимальные размеры конструкций. Пантеон достиг предельных возможностей бетонно-кирпичной техники. Купол того же размера, выполненный из тончайших железобетонных сводов, не показался бы нам столь же масштабно величественным.
Как показали исследования
Шеданна (1892-93 гг.), сооружение было воздвигнуто при императоре Адриане в
110-
Итак, основной архитектурной идеей и одновременно конструктивной достопримечательностью сооружения является купол, а вслед за тем портик храма, поэтому анализ соотношений, определяющих их размеры, должен быть нашей главной задачей.
Если мы опишем около квадрата со стороной, равной ста г. ф., окружность, то такая окружность определит в интерьере размеры круглого зала Пантеона. Сто г. ф. являются в данном случае модулем - исходным размером для построения архитектурной формы сооружения. Толщина стен ротонды определяется разностью между ее внутренним диаметром и стороной вписанного квадрата(20).
Греческий фут равен
Ширина портика Пантеона,
измеренная изнутри, т.е. без учета толщины колонн, равна тем же
Портик членится внутренними колоннами на три части. Средняя, обрамленная колоннами, приравнена большому отрезку золотого сечения, а боковые нефы - малому. Глубина портика приравнена ширине его средней части.
Пропорции "конечной
формы" плана Пантеона заключаются в соотношении наружного диаметра ротонды
и полной его длины с портиком, равном . Соотношение ширины
портика и диаметра ротонды равно 
.
Большой ордер в интерьере Пантеона приравнен по высоте малому отрезку золотого сечения по отношению к радиусу ротонды. Малый ордер соотносится с большим как сторона и диагональ квадрата. При этом общая высота двух ордеров оказалась лишь на незначительную долю больше ее радиуса. Пята свода расположена на уровне карниза малого ордера. Таким образом, общая высота интерьера равна его диаметру с очень небольшим превышением.
Высота Пантеона до
верхнего карниза приравнена
Говоря о типологических
особенностях Пантеона, нельзя не отметить наличие в римской архитектуре других
круглых в плане и перекрытых куполом сооружений. Наличие установившихся традиций
в сооружении купольных зданий может быть наглядно подтверждено, например,
сравнением Пантеона с купольным залом в термах около Бай, сооруженным еще во
2-ой половине I в. до н. э., т.е. за два столетия до Пантеона. Тот зал
освещался так же как Пантеон, через отверстие в зените купола. Его диаметр был
ровно в два раза меньше купола Пантеона и равен
Базилика Максенция на плане римского
Форума привлекает внимание своими размерами. Мощными бетонными сводами была
перекрыта площадь в
Помимо базилики Максенция в Риме существовали еще также очень большие по размерам базилики: Эмилия, Юлия, Ульпия. Но эти базилики существенно и принципиально иные, чем базилика Максенция. Своды ее центрального нефа покоятся всего на четырех внутренних опорах, базилики же Эмилия, Юлия и Ульпия членятся на нефы десятками колонн. Генезис формы этих базилик, очевидно, связан с перистильными композициями, периптером и его интерьером. Базилика же Максенция не следует этому пути развития и столь же очевидно связана с относительно новыми типологическими формами. Опереть своды на широко расставленные опоры оказалось возможным в связи с использованием крестовых сводов, получивших в Риме широкое распространение. В частности, при помощи большого масштаба крестовых сводов перекрывались центральные залы римских терм.
Для уяснения архитектурных форм базилики Максенция, равно как и Пантеона, нет необходимости привлекать небольшие и неточно датируемые памятники Сирии и Малой Азии. На наш взгляд, как базилики, так и Пантеон являются продуктом чисто римской строительной культуры.
Строительство базилики было самым крупным предприятием Максенция, который за пять лет своего правления успел сделать очень много для блеска и красоты императорского Рима. Если конструктивной, а равно и архитектурной особенностью Пантеона является купол невиданных ранее размеров, то базилика замечательна гигантского размера крестовыми сводами.
Надо сказать, что в конструкциях опор, на которых покоились крестовые своды базилики, наблюдается некоторая странность. Дело в том, что основания сводов поддерживались кронштейнами, выступающими из торцов могучих поперечных стен боковых нефов. Эти стены членят малые нефы на три части и несут превосходные кессонированные коробовые своды. Странность заключается в том, что эти кронштейны подперты мощными гранитными колоннами, которые сами по себе могли бы выдержать нагрузку от сводов без каких бы то ни было кронштейнов, а кронштейны, по-видимому, могли бы удержать своды без всяких колонн. Некоторые авторы высказывают предположение, что эти колонны были чисто декоративными, имея в виду, что их можно убрать, не обрушив своды. Однако это утверждение вряд ли справедливо, ведь передавая очень большую нагрузку от огромного бетонного свода через посредство кронштейна на торец поперечной стены нельзя было рассчитывать, несмотря на ее монументальность, на статическое равновесие при неравномерной осадке этой стены. В связи с несимметрично расположенной сосредоточенной нагрузкой от свода и были установлены колонны, способные принять на себя всю тяжесть свода, стена же работала благодаря этому нормально и в то же время воспринимала тот распор, который мог появиться в связи с теми или иными деформациями свода. (Высказанное суждение следует проверить на основе детального изучения конструкций сооружения и его фундаментов).
Заметим здесь же, что если мы правы и римские зодчие действительно осознали статические особенности работы монолитной стены с вплотную к ней примыкающей каменной колонной, то это могло бы пролить свет на смысл, рождение и генезис многих архитектурных форм позднеримской, византийской, а вслед за ней романской архитектуры.
С приходом к власти императора Константина базилика Максенция была закончена. Однако ее композиция была переосмыслена и в результате сооружена дополнительная апсида по поперечной оси сооружения. В этом сопоставлении продольной и поперечной осей можно видеть зачатки идеи центричной композиции типа крестово-купольных базилик Византии.
Анализ основных соразмерностей плана базилики Максенция дает следующие результаты.
Ширина базилики изнутри равна
Соотношение ширины базилики и ее длины в интерьере равно отношению стороны квадрата и его диагонали. Эти соотношения в сопоставлении друг с другом определяют толщину опорных пилонов.
Ширина малых боковых нефов и среднего
нефа соотносится как .
Соотношение ширины базилики,
измеренной извне по нартексу, с ее полной длиной равно .
Приведенные соразмерности, как Пантеона, так и базилики Максенция свидетельствуют о практическом применении трактата Витрувия и о самом методе творческого труда римского зодчего.
Напомним, что трактат Витрувия относится к 40-20 годам I века до н. э. Античных рукописей до наших дней не дошло. Пятнадцать известных списков труда Витрувия датируются IX-XI вв., а еще целый ряд списков относится к XIII-XV векам. Это свидетельствует, что античная теория архитектуры не теряет своего значения для позднего Рима, Византии и всего Средневековья.
Витрувий говорит не только о наличии соразмерностей сооружения, но и методе его начертания в определенной последовательности. Необходимо вчитаться в текст Витрувия. Он говорит, что «ихнография есть надлежащее и последовательное применение циркуля и линейки для получения очертаний плана на поверхности земли» (книга I, гл. II, п. 2). Нетрудно увидеть прямое противоречие: Витрувий говорит о циркуле и линейке и одновременно о поверхности земли, на которой устанавливаются контуры сооружения уже в натуральном масштабе, для чего никакие циркуль и линейка уже не годятся. В этом случае необходим достаточно большой шнур. Очевидно, сказанное Витрувием равно относится к проектированию, составлению чертежа, и к разбивке сооружения уже на строительной площадке.
Мы должны обратить внимание на последовательность построения формы сооружения и конечно, прежде всего, на первое звено построения: "Соразмерность есть ... соответствие отдельных частей всего целого одной части, принятой за исходную" (там же, п.4).
Исходная для всего построения величина, очевидно, устанавливается по заданию заказчика в силу тех или иных "внешних" причин и соображений. (В современной практике это - "плановое задание", нормы и габариты оборудования... Иначе говоря, современный нам архитектор имеет дело с множеством нормативов, что и обусловливает его тщетные попытки гармонизации форм возводимого здания.)
Храм Софии в Константинополе,
сооруженный в эпоху Юстиниана зодчими Анфимием из Трала и Исидором из Милета в
532-
Купол, покоящийся на четырех опорах посредством треугольных парусов или пандативов, а иногда и тромпов, был важнейшей типологической и конструктивной формой, характерной для византийского храмостроения. (Строительство базиликальных храмов без купола также имело место в ранний период истории Византии, но в последствии не было распространенным.)
Именно эта конструктивная форма купола на пандативах была положена в основу архитектурного замысла при строительстве уникального храма - храма Софии Премудрости Божией. Сферический купол как нельзя лучше подошел для символической, образной характеристики христианского храма. Купол Софии принципиально отличен от купола Пантеона. Рим создает мощный, конструктивно понятный купол, Византия же лишает купол Софии массы и веса - это небосвод над интерьером храма .
В храме Софии именно на куполе было сосредоточено все внимание зодчих. Вполне закономерно купол явился исходной формой, которая в последующих построениях определила меру всех соразмерностей сооружения. По терминологии Витрувия, размеры купола явились "исходным размером", но не тектонических форм сооружения, а размеров куполов, образующих своего рода "гармонию сфер". Купол лишается массы и веса, повисает над головами молящихся своего рода небосводом.
Зодчие разрабатывают структуру и гармонию не конструктивной оболочки, а пространства интерьера. Квадратный в плане центр храма перекрывается куполом, в основании которого кольцо света - часто расположенные окна вовсе лишают купол массы и весомости. Треугольные паруса, которым надлежит передать тяжесть купола на столбы, повисают как бы без нагрузки и делают свое дело незримо: столбы не обозначены в интерьере, а прячутся за стенами, облицованными мрамором, рисунок которых как бы подчеркивает легкость и невесомость самой стены.
Пространство центральной части храма развивается по оси восток - запад полуциркульными "апсидами" того же радиуса, что и центральный купол. Восточная и западная грандиозные "апсиды" в свою очередь членятся каждая тремя меньшими апсидами. В результате перед посетителем развертывается хотя и сложное, но ясное по структуре и форме перекрытое куполом и полукуполами гармоничное пространство храма с оболочкой, лишенной материальности. Такой принцип ограждения пространства храма зрительно предельно легок, к тому же своды покрыты сияющими золотым фоном мозаиками.
Обратим внимание прежде всего на горизонтальную проекцию купола в плане сооружения. Это точный круг, вписанный в квадрат. Но купол получил со временем искаженную форму. Имеющиеся отклонения объясняются разрушениями и восстановлением купола, а так же деформациями, которым подвергалось сооружение в силу имевшего место распора или сейсмических толчков. За длительный срок существования храма причин для искажения формы купола имелось немало. По замыслу купол сферический и в плане очерчивается окружностью. Первоначально это так и было.
Основание купола лежит на
"кольце", образованном смыкающимися грандиозными
парусами-пандативами, посредством которых тяжесть купола передается на четыре
опоры. В настоящее время купол имеет диаметр, равный в направлении восток -
запад
Первоначальный купол, упавший во
время землетрясения, был выполнен как продолжение сферической поверхности
парусов и таким образом был менее чем полусферой и более плоским, чем купол,
сооруженный позднее. Мы же должны, устанавливая диаметр первоначального купола,
приравнять его стороне подкупольного квадрата, измеренного по основанию стен.
Стороны подкупольного квадрата по вышеупомянутому обмеру равны удивительно
точно
В итоге мы с полной достоверностью
устанавливаем, что купол храма Св. Софии имел диаметр
Любопытно проследить, что если
диаметр купола храма Св. Софии равен
В византийском храмостроительстве существовала устойчивая традиция, следуя которой зодчий или ктитор, приступавший к возведению храма, устанавливая его модульный размер, исходили из уже существовавших храмов и, прежде всего из размеров центрального купола.
Начиная анализ с измерения купола, а затем и несущих его столпов, мы следуем издавна установившимся традициям византийского зодчества.
Прекрасным свидетельством тому, что подобная последовательность построения соразмерностей храма действительно имела место при составлении чертежа или разбивки плана в натуре, служит стихотворение Константина Родосского (или Родия) - византийского писателя, жившего в Х веке(25). В тексте этого стихотворения дано отчетливое описание строительства ц. Двенадцати Апостолов в Константинополе, буквально в той же последовательности, как мы предполагаем.
Оно начинается с описания, как на строительной площадке определяется центральный подкупольный квадрат, как вслед за тем устанавливается положение четырех столбов по углам этого квадрата. Дается ему наименование "мезомфалос" (m e s o m j a l o d ), что значит "сердцевина", "средоточие". В стихотворении подчеркивается первостепенное значение главного купола с изображением Христа.(26)
Продольная ось храма ориентирована на восток - запад, поперечная - на юг - север (схема соразмерностей 1). Заметим, что в христианском храмостроительстве ориентация восток - запад выдерживается не очень точно. Возможно, что продольная ось храма устанавливалась в направлении восхода солнца на время закладки фундаментов храма, к тому же обусловленного контуром горизонта на месте строительства. Храм Св. Софии ориентирован с отклонением на юг примерно на 40» (!).
Затем мы должны определить положение квадрата, имеющего сторону, равную проектному диаметру центрального купола и описанного около круга, являющегося его горизонтальной проекцией
Границы всего храма в интерьере определяются при помощи построенного нами квадрата и его диагоналей. Продольный размер определяется весьма точно полудиагональю исходного квадрата. Поперечный размер также очень точно - диагоналями его половины. В результате мы получаем план храма в целом весьма близкий к квадрату, но несколько отличающийся от него. Математическое выражение в цифрах этой пропорции довольно сложно, что и доказывает геометрическое происхождение этой соразмерности.
Если сторона исходного квадрата равна
100, то продольный размер храма будет равен 
, а поперечный 
. Следовательно, отношение сторон равно 
. Подобное построение мы можем проследить в
плане некоторых других византийских и русских храмов. Это очень тонкое,
нюансовое отношение надо при последующем анализе, что называется, "взять
на вооружение".
Интересно отметить, что при таком построении боковых нефов поперечные размеры храма и соотношение сторон те же, что и у Парфенона. Иначе говоря, храм Св. Софии может служить "футляром" для прославленного храма античности. Что это - случайность, преднамеренное подражание или следствие общего метода построения архитектурной формы? Об этом можно только гадать.
Апсиды, покрытые полукуполами, имеющими тот же диаметр, что и главный купол, фланкируют его с востока и запада, принимая на себя возможный распор. Центры апсид отступают на 1/6 радиуса купола. Этот размер определяет толщину подпружных арок, оставшихся так и не выявленными, которые без раскреповки переходят в полукупола больших "апсид". (Именно этот размер был ранее определен нами ошибочно на основании неточного чертежа храма.)
Алтарный проем в восточной апсиде и равный ему проем с запада, в котором размещается центральный вход, определились стороной квадрата, вписанного в полукружие, очерчивающее большие апсиды.
Центральное звено боковых нефов приравнено стороне квадрата, вписанного в окружность - горизонтальную проекцию центрального купола. Тем же построением определяется аркада в подпружных северной и южной арках, а так же внутренняя грань опорных пилонов.
Крайние восточные в западные звенья боковых нефов приравнены 1/4 части длины храма. Тем самым установлена толщина пилонов.
Ширина малых нефов приравнена половине ширины центрального нефа. Соотношение, ставшее традиционным и ранее наблюдавшееся у базиликальных сооружений.
Малые полуциркульные своего рода экседры или конхи, перекрытые полукуполами, очерчиваются радиусом, равным радиальным размерам парусов в плане. Алтарная апсида очерчена тем же радиусом, что и "конхи".
Чем вызвано, что стены храма имеют разную толщину, остается необъяснимым, хотя благодаря этому отношение длины и ширины храма, измеренных изнутри, оказалось равным отношению длины и ширины храма, измеренных извне (не считая нартексов).
Ширина внутреннего нартекса приравнена ширине малых нефов. Внешний нартекс, сооруженный впоследствии, имеет ширину в отношении к ширине внутреннего нартекса в "золотом сечении".
Нартексы несколько меньше полной
ширины храма (и приравнены с очень небольшом приближением удвоенной стороне
подкупольного квадрата), что соответствует отношению ширины храма, измеренной в
пределах нартекса, и его длины как 
.
"Ихнография" плана получает
тем самым прекрасную иллюстрацию. Начальное звено построения - стофутовый купол
и конечная форма плана определяются отношением (схема соразмерностей 2), что
полностью соответствует указаниям Витрувия.
Вертикальные размеры храма по традиции устанавливаются непосредственно из размеров плана сооружения. Традиция эта появилось из трудностей, возникающих при построении иррациональных геометрических отношений в вертикальной плоскости. Конечно, подобные трудности для изощренных геометров, какими были Исидор и Калликрат не слишком значительны, но традиция есть традиция. При становлении плана сооружения, его разбивке и закладке фундаментов происходит "рождение" постройки, как говорит Барбаро, комментируя Витрувия(27).
Изображение фасада или внутреннего вида здания, сооружения, должно соответствовать плану, ибо в противном случае вещь рождающаяся и вещь растущая вверх, не будут одним и тем же. Это суждение означает, что при построении вертикальных размеров сооружения приходится искать им соответствия в размерностях плана.
Первоначальный купол храма обрушился.
Предполагается, что он был гораздо более плоским и имел радиус кривизны тот же,
что и паруса. (И в этом случае радиус кривизны купола был бы тот же, что и у
Пантеона в Риме.) Но это, однако, не означает, что радиус купола в его
основании сколько-нибудь отличался от
Основание купола или кольцо
смыкающихся парусов расположено на высоте, соотносящейся к стороне
подкупольного квадрата как 
.
Вторым важнейшим размером в разрезе
храма является высота, на которой покоятся: пяты подпружных арок, основания
восточного и западного полукуполов, а также полукуполов, перекрывающих малые
апсиды и алтарного и, соответственно, входного свода. Основание всех этих арок
и сводов расположено на высоте в отношении к пролету подпружных арок или
диаметру купола (.
Таким образом, пролет подпружных арок
соотносится с их высотой как . Напомним, что отношение получило
в византийской и древнерусской архитектуре большое распространение, возможно в
связи с близостью его к решению задачи удвоения куба 
, а также к
отношению двойного золота 
.
Эти немногие данные определяют основные размеры сооружения по высоте.
Проведенный анализ соразмерностей Софии Константинопольской - этого удивительного, своеобразного, прекрасного храма Византии, дает возможность обратить внимание на значение труда Витрувия для архитектуры Византии.
Храм Софии в Салониках сооружен через два века после Константинопольской Софии. Уже нет речи о воздушном геометризме, о нематериальности и невесомости архитектурных конструкций. Если у храма Константинопольской Софии мы измеряли пространственные построения, то теперь у Софии в Салониках купол покоится на четырех мощных сводах, которые лежат на четырех массивных пилонах, их размеры мы и должны определить.
Ц. Софии в Салониках является дальнейшим и надо сказать далеко ушедшим от прототипа, каким является храм Софии Константинопольской, образцом византийской церкви. В ней мы еще не видим сформировавшегося типа крестово-купольной постройки, однако, узкие поэтажные арочные проемы в массивных пилонах уже являются своего рода обходным кулуаром, а пилоны в плане приобретают вид четырех подкупольных столбов. Конечно, этот храм не одинок, формирование типа крестово-купольного храма, а равно и крестового храма иллюстрируется рядом интереснейших сооружений той же эпохи, как, например, Календер Джами в Константинополе, ц. Успения в Никее и др.
Ста футам у храма Софии в Салониках
приравнены полная ширина храма в интерьере от южной до северной наружных стен.
Диаметр центрального купола в три раза меньше диаметра купола Софии
Константинопольской. Соответственно куполу сторона подкупольного квадрата равна
Внутренняя грань западной стены устанавливается диагональю подкупольного квадрата, восточная стена, определяющая положение апсид, устанавливается той же диагональю за вычетом стороны подкупольного квадрата.
Размеры четырех подкупольных столбов определяются окружностью, описанной вокруг подкупольного квадрата. Это построение получило впоследствии и в древнерусской архитектуре очень широкое распространение. Сторона больших опорных пилонов с арочным проемом определяется диагональю подкупольного квадрата за вычетом радиуса центрального купола.
Южная и северная боковые ветви крестовой в плане центральной части храма приравнены 1/3 стороны подкупольного квадрата. Западная ветвь креста приравнена 2/3 стороны подкупольного квадрата.
Ширина обходного нефа приравнена 1/3 ширины центрального крестообразного пространства в пределах его угловых пилонов. Боковые нефы в сумме со столбами приравнены стороне подкупольного квадрата.
Наружные стены имеют толщину, приравненную к стороне квадратных столбов.
Глубина алтаря приравнена стороне подкупольного квадрата.
Ширина сооружения, измеренная извне,
и его длина, соотносятся как .
Три апсиды несколько уже храма и не соответствуют его нефам, что может быть объяснено желанием зодчего придать ширине и длине храма более контрастное соотношение, в данном случае приравненное золотому сечению.
Проследить многовековую эволюцию развития архитектурных форм в Византии с точки зрения строительного ремесла, математического вооружения зодчих было бы, конечно, очень интересно и явилось бы далеко еще не исчерпанным источником наших знаний о византийской науке и культуре. Но это большой, капитальный труд. Мы же спешим проследить "эстафету" архитектурной культуры от одного памятника до другого. В данном случае храм Софии в Салониках, как мы считаем, является отнюдь не соседним, но звеном цепи преемственности, связывающей русскую архитектуру XI века с Византией.
Храмы Киева и Великого Новгорода
София Киевская и София
Новгородская. Оба храма сооружены почти одновременно. Ярослав Мудрый
закладывает храм Софии в Киеве в
Но все же следует заметить, что оба храма оригинальны и близкого образца в пределах Византии не имеют. Их своеобразие заключается во множестве пересекающихся нефов и крестовых столбах. Богослужение нельзя было наблюдать из глубины храма, а хоры сооружались без казалось бы должного внимания к алтарю. И если вглядываться в структуру храмов, то невольно приходят в голову фрагменты частично вскрытых раскопками руин Большого дворца в Константинополе, имеющего подобную нашим храмам мелкоячеистую структуру. Эта аналогия заставляет нас признать храмы Софии на Руси и особенно Софию Киевскую храмами - дворцами и недаром на хоры вел отдельный вход и живопись, сохранившаяся на лестнице, имела исключительно светское, а не религиозное содержание. К тому же, хоры освещались верхним светом и второй ярус галереи служил прекрасным балконом.
За длительный срок существования храмы неоднократно достраиваются, перестраиваются, ремонтируются, реставрируются. Изучая их архитектуру, прежде всего задаешься вопросами: как же выглядел храм первоначально и что в нем возникло впоследствии? Но в обоих случаях имеющиеся проекты реконструкции первоначального облика либо игнорируются, либо в чем-то дополняются или исправляются. Молодые исследователи заново вновь и вновь обращаются к решению этой задачи.
Общий размер храма без
больших папертей приравнен
Они могли возникнуть вскоре после возведения сооружения или даже во время строительства. Исследование, внимательное изучение сооружения может установить время возведения той или иной его части, но с известной степенью точности, а вот это-то и является подчас причиной возникновения дискуссий и нескончаемых споров. В этих спорах и мы принимаем деятельное участие. Но нам в первую очередь важны не изменения в архитектуре этих замечательных храмов, а первоначальный проектный, зодческий замысел и только вслед за тем последовательная история его существования.
У Софии Киевской обсуждаются последовательность сооружения папертей и лестничных башен, у Софии Новгородской спорным является также время сооружения папертей и особенно их второго этажа. Вопрос для историка архитектуры стоит так: каков был в том и другом случае зодческий замысел и что относится к его изменению, как в процессе строительства, так и впоследствии?
Наряду с поисками литературных источников, материальных свидетельств, особое значение приобретает архитектурно-композиционный анализ.
Если мы внимательно посмотрим на последний проект реконструкции первоначальных архитектурных форм храма Софии Киевской, то увидим, что окружающие его паперти своими размерами как бы умаляют значение самого храма. Они лишь на толщину стены уже главного нефа. Они кажутся пристроенными впоследствии. Это предположение становится уверенностью, когда мы обратим внимание на то, что малая галерея, окружая храм полностью, затемнена широкими папертями. Следует предположить, что наружные паперти сооружались вопреки или лучше сказать, сверх того, что было замыслено зодчим.
Естественно было бы высказать предположение и о том, что малые галереи храма первоначально были одноэтажными и тогда храм в уровне хоров получил бы хорошую освещенность . Эту мысль подтверждают обмерный чертеж Д. Иванова и реконструкции Ф. Солнцева, Н. Брунова, А. Новицкого и др. Однако если бы это было так, то галерея безусловно была бы отрезана от храма осадочным швом. О наличии такого шва мы не осведомлены, а поэтому не должны на таком варианте настаивать. Северо-западная башня могла быть сооружена ранее папертей, так как она может быть связана со вторым ярусом галерей непосредственно. (Диаметр ее приравнен 1/2 диагонали подкупольного квадрата.)
Юго-западная башня не имеет непосредственной связи со вторым ярусом галереи, ее диаметр равен ширине папертей и сооружена она была, по-видимому, одновременно с ними, хотя полностью исключить вариант сооружения и этой лестничной башни вне связи ее с папертями нельзя. Достаточно вспомнить постановку подобных башен впоследствии в ХII в. у некоторых храмов Новгорода и Владимира. Наружные же паперти храма, исходя из композиционных соображений, не могут быть отнесены к первоначальному замыслу зодчего. И нет нужды в том, что очень авторитетные ученые настойчиво утверждают, что паперти якобы были сооружены одновременно с самим собором. Несомненно, зодчий, сооружая основной корпус собора, о них еще и не подозревал. Да и сами паперти могли быть сооружены не одновременно, а последовательно, прежде всего западная, затем южная и лишь затем северная. Такая последовательность композиционного мышления зодчего нам кажется несомненной. Об этом же говорят проекты реконструкции храма, предложенные Д. Ивановым, Ф. Солнцевым, Н. Бруновым, А. Новицким, К. Конантом, И. Моргилевским. И аналитические исследования пропорций говорят о том же.
В строгом соответствии с
рекомендациями Витрувия, мы начинаем с первичного размера, заданного заказчиком
или установленного зодчим. Этим размером был диаметр купола или сторона
подкупольного квадрата Софии Киевской -
Построение подкупольного
квадрата не очень точно. Строго говоря, это не квадрат, а едва выраженный ромб,
и его диагонали разнятся одна от другой на 20-
Квадратная сердцевина
крестчатых столбов приравнена своей диагональю к размеру паруса и равна
разности полудиаметра подкупольного квадрата и его полустороны. Тому же размеру
равна толщина стен храма. Столбы приобретают крестчатую форму при помощи
диагонали полуквадрата сердцевины столба, отмеренной от его середины.
(Построение отношения "золотого сечения": стороны квадрата относятся
к диагонали полуквадрата в сумме с половиной его стороны как 
)
Окружающие подкупольный квадрат со всех четырех сторон малые нефы, в том числе и восточный алтарный неф, построены подобным же образом, ширина их в сумме со столбом равна разности между диагональю подкупольного полуквадрата и половиной его стороны. Тот же прием геометрического построения "золотого сечения" мы встречаем в пропорциях плана ц. Софии Константинопольской.
Ширина алтарного нефа в пределах второй раскреповки у основания апсид приравнена половине ширины большого нефа.
Центр большой апсиды определяется вершиной равностороннего треугольника со стороною, равной восточной стороне подкупольного квадрата и совмещенной с ней. Диаметр апсиды равен высоте того же равностороннего треугольника. С построением пропорций малых апсид можно познакомиться по чертежу.
При помощи диагонали центрального звена уже построенного нами первого южного, а также северного и западного нефов, с учетом толщины столбов устанавливаются соответственно ширина соседних нефов храма. При этом ширина вторых малых нефов оказывается очень близкой ширине соседних первых нефов, но не равна им.
Малые нефы по ширине несколько разнятся и разница эта соответствует в ту же меру разнящимися друг от друга диагоналями, при помощи которых производится построение.
Храм в интерьере по
ширине в пределах всех пяти нефов и четырех поперечных нефов в сумме с апсидой
имеет одну и ту же величину. Соотношение выдержано весьма точно, длина храма
превышает его ширину лишь на 15-
Равносторонний треугольник со стороной, равной ширине храма, определяет, если принять за его основание внутреннюю грань западной стены, центр главной апсиды. Построение выдержано не совсем точно, что объясняется уже отмеченными выше ошибками в построении плана.
Необходимо отметить, что
ширина, а равно и длина храма, измеренная без галерей, но с наружными
пилястрами, равна
Извне длина храма
относится к его ширине как . Таким образом, храм и без больших
папертей получает завершенную пропорциональную форму.
Диаметр северной лестничной башни (изнутри) приравнен полудиагонали подкупольного квадрата. Диаметр южной башни (изнутри) приравнен диаметру центральной апсиды.
После сооружения больших
галерей изнутри длина и ширина храма соотносятся как . Извне
соотношения сторон храма (без апсид) равно . В разрезе, опять же в
полном согласии с Витрувием, храм имеет прямое соответствие с его размерами в
плане.
Высота храма равна его длине (без окружающих его галерей). Длина измеряется от западной стены и до центра апсиды, высота - от пола до основания купола.
Барабан центральной главы
храма имеет соотношение высоты к диаметру, равное . Сечение
купола отличается от строго сферической формы, для его геометрического анализа
необходимы натурные шаблоны. Основание барабана располагается по высоте, равной
половине ширины храма, измеренной с первоначальными галереями (см. схему).
Шелыга свода, перекрывающего большой неф, располагается на высоте, равной ширине или длине храма в пределах его трех центральных нефов.
Пята подпружных арок и пята сводов расположены на высоте, равной половине длины храма или расстояния от центра храма до западной стены.
Высота апсиды равна полной ее глубине. Неправильная форма поверхности полукупола выполнена в расчете на мозаичное изображение ("Оранта"), благодаря чему оно при том или ином освещении получает ряд живописных бликов. Основание полукупола, перекрывающего апсиду, заложено на высоте, равной расстоянию от центра храма до центра апсиды. Хоры расположены на высоте, равной половине высоты главных подпружных арок, или, с некоторым приближением, ширине большого нефа.
По поводу архитектурных
форм храма Софии в Новгороде спор ведется, как мы уже сказали, о времени строительства
наружных папертей, апсид у них и о времени надстройки над ними второго яруса. С
точки зрения авторского зодческого замысла, задача реконструкции решается
достаточно убедительно (см. илл. 8 на вкладке). Мы и теперь настаиваем на
ранее, еще в 1944-
Храм имел паперти сооруженными одновременно с храмом и принадлежащими к первоначальному зодческому замыслу. Об этом свидетельствует высота храма, приравненная к его длине, измеренной вместе с папертью; наличие наружных порталов на фасадах храма во втором ярусе и др.
Приделы в восточной части южной и северной паперти были сооружены впоследствии. Апсиды, сооруженные изначально, не могли бы иметь в своем основании следов ранее существовавших крестчатых столбов; западная стена приделов или восточная стена папертей не могла быть запроектирована зодчим на столь не обусловленном структурой храма месте.
Изначально паперти храма
были одноярусными. При двухэтажных папертях не было надобности сооружать
аркбутаны, обеспечивающие разную осадку стен, что было необходимо при различной
высоте стен; сооружение второго яруса затемняет храм и даже обесценивает ранее
сделанные окна. Перекрытие второго яруса многоцентровой полуаркой большого
пролета (
Гончарные горшки в забутовке пазух сводов, перекрывающих первый ярус папертей, свидетельствуют о том, что второй ярус папертей воздвигался позже, уже следующим поколением зодчих. Как ни пытаться, но объяснить такую несообразность, как строительство монументальных тяжелых стен второго яруса паперти на глиняных пустотелых горшках в их основании, положенных для облегчения нагрузки на своды, небрежностью, забывчивостью архитектора никак нельзя.
Предложенный нами ранее проект реконструкции храма остается не опровергнутым, хотя и недоделанным в части устройства арочных проемов в приделах папертей, как равно наружного входа в башню лестницы. Кроме того, необходимо заметить, что в процессе исследования храма остались нерешенными детали примыкания башни в приделах второго яруса к стенам паперти, а также неясен характер использования западного звена Мартирьевской паперти.
Основное расхождение с предложенным нами проектом изложено Г. М. Шнайдером в статье "Первичный замысел и последующие изменения галерей и лестничной, башни Новгородской Софии".(29) Оно заключается в ошибочном указании на одновременность сооружения второго яруса галерей. С нашей точки зрения, второй ярус был сооружен уже впоследствии, быть может, вскоре, но после окончания строительства и вопреки первоначальному замыслу.
Заманчивым предположением является желание новгородцев соорудить свой храм Софии в размер Софии Киевской. И в самом деле, длина и ширина обоих храмов оказались совершенно точно равными у обоих храмов. Сам храм Софии в Новгороде несколько меньше, но сооружение больших папертей позволило достичь размеров в плане храма Софии Киевской. Это объясняет наличие широких папертей у храма в Новгороде и свидетельствует о наличии у киевского храма малых галерей. Убедившись в превосходстве больших папертей на примере новгородского храма, киевляне в свою очередь сооружают широкие паперти и у своего храма как раз того же размера, что и новгородцы.
Установленные нами соразмерности и пропорции плана храма Софии Новгородской следующие.
Подкупольный квадрат,
имеющий сторону, равной диаметру купола, является "началом"
последующих построений и приравнен
Диаметры купола и
барабана главы равны 6,10 -
Размеры южного и северного нефов приравниваются половине ширины центрального нефа или половине стороны подкупольного квадрата, то же построение малых нефов можно получить, приравняв их вместе со столбами половине диагонали подкупольного квадрата.
Размеры западного и восточного (алтарного) нефов устанавливаются при помощи диагонали подкупольного полуквадрата.
Заметим, что два последних построения повторяют построение контура плана Софии Константинопольской. Центральная часть храма в пределах подкупольного квадрата, четырех столбов и окружающих его со всех четырех сторон малых нефов в точности повторяет пропорции храма Софии Константинопольской, в пределах его наружных стен.
Все малые нефы строятся последовательно с помощью диагоналей больших звеньев малых смежных внутренних нефов, причем совпадение этого построения с обмером в натуре полное. Ширина этих нефов различная, но точно соответствует диагонали среднего звена плана соседних нефов.
Глубина большой апсиды равна ее диаметру, в свою очередь равному ширине большого продольного нефа.
Ширина папертей южной (Мартирьевской), северной и западной (Корсунской) приравнивается каждая ширине большого нефа. Однако в связи с неточностью построении в натуре подкупольного квадрата, а, следовательно, и больших нефов, паперти по размерам соответственно отличаются друг от друга. Так, западная паперть несколько шире других и точно равна диаметру апсиды, что к тому же дает возможность удобнее разместить круглую лестницу в звене паперти, отличном в плане от квадрата. Таким образом, неточность, допущенная в построении подкупольного квадрата, явилась причиной преувеличения диаметра апсиды, а вслед за тем и преувеличения размера западной паперти. Все это красноречиво рассказывает нам о методах разбивки сооружения в натуре.
Внутренний диаметр лестницы равен ширине двух малых южных нефов. Круглый столб лестницы имеет диаметр, равный ширине маршей.
В интерьере полная ширина храма соотносится с его длиной, как сторона равностороннего треугольника и его высота.
Извне ширина храма
соотносится с длиной (без апсид) как .
Соразмерности храма в разрезе.
Высота храма с некоторым
приближением, обусловленным неувязками в построении, равна его длине. Высота
храма равна
Соотношение ширины храма
(без паперти) и высоты равно .
Верхний карнизик в интерьере храма располагается на половине его высоты.
Основание свода апсиды расположено на этом карнизике, повышенном на высоту солеи.
Высота храма до основания барабана центральной главы равна длине храма от западной стены до центра апсиды.
Пята подпружных арок расположена на высоте, равной ширине храма в пределах трех центральных нефов.
Хоры расположены на высоте, равной половине ширины храма.
Первый карнизик расположен на высоте, равной ширине малого нефа в сумме с примыкающими к нему столбами.
Барабан центральной главы по высоте, измеренной внутри храма, равен его диаметру. Окна барабана по высоте равны ширине малых нефов или полудиагонали подкупольного квадрата.
Пяты свода, а равно и арок под хорами, расположены на высоте, равной ширине двух малых нефов.
Более детальное рассмотрение соразмерностей этих двух древнейших храмов Руси может многое рассказать об истории строительного искусства и ремесла. Пропорциональный анализ является далеко не исчерпанным источником сведений, относящихся к истории отечественной архитектуры.
Подводя итог нашей "эстафете", мы обнаруживаем в предельно разнообразных архитектурных формах ее звеньев неизменный геометризм построения. Математика, геометрия являются "оформлением" строительной деятельности, без которых она просто невозможна. Недаром геометрия оказалась впереди других наук и вооружила человека в его строительной, как, впрочем, и всякой иной созидательной деятельности.
Евклид и его геометрия оказались без особых изменений на вооружении зодчих Египта (даже в доевклидовские времена), Греции, Рима, Византии, Древней Руси. И мы не побоимся высказать, казалось бы, парадоксальное суждение о том, что геометрия Евклида сохраняет свое значение и для современного строительства. Геометрия помогает не просто строить, она, выполняя технические функции, одновременно гармонизирует форму и, более того, служит одним из важных средств образной характеристики произведений архитектуры.
Приведенные выше наблюдения дают повод для размышлений и инженеру-строителю, и архитектору-художнику. Уровень математических знаний, с которыми мы встретились в процессе пропорционального анализа, остается в пределах элементарных геометрических закономерностей и простейших арифметических чисел. Дело здесь не в умении оперировать сложными математическими вычислениями и построениями, а в простейших "консонансных" числах, доступных восприятию органами чувств человека.
Мы, анализируя пропорции
сооружений исторического прошлого, как бы наблюдаем за действиями зодчего. Он
не прибегает к измерению частей здания, а он строит их на основе простых
законов соразмерности; он в принципе прибегает к мерам длины лишь однажды,
определяя исходный размер для последующей цепочки соразмерностей. Во всем этом
мы имели возможность убедиться. Этот размер определялся "по образцу",
примеру ранее сооруженных зданий и выражался округлым значением мер длины. Мы
встретились со 100-футовым размером Парфенона; через шесть веков (!) тот же
100-футовый размер применен строителями Пантеона Рима; еще через два века в том
же Риме сооружается базилика Максенция и ее размер определяется теми же ста
футами; еще через два века купол Софии Константинопольской оказывается равным
тем же
Мы накопили много примеров использования этого размера. Факт распространения этой меры - ста греческих футов - во времени от Парфенона V в. до н. э. до Киевской Руси XI-XII веков н. э. и на территории от Рима до Новгорода свидетельствует о своеобразной градостроительной дисциплине, единой шкале масштабности и устойчивости меры длины.
илл. 1
1.Hans R. Hahnloser. Villard de Honnecourt. Austria, Graz, 1972. Taf. 35 - 37.
2.Анализ рельефа Хасира
содержится в докладе и трудах XXXII научной конференции Московского
архитектурного института (март
Рисунок из альбома Виллара де Гоннекура.
3.Б. А. Рыбаков. Архитектурная математика древнерусских зодчих. "Советская археология", « 1, 1957, с. 84-86.
4.В Каирском музее хранятся еще несколько подобных изображений, выполненных той же техникой, но значительно хуже сохранившихся. Там же имеются несколько подлинных жезлов, которые ждут тщательного изучения.
Зодчий Хасира. Схема соразмерностей 1.
Зодчий Хасира. Схема соразмерностей 2.
5.История Древнего мира. Т. 1. Древний Восток. М., 1936, с. 176.
6.К. Н. Афанасьев. Построение архитектурной формы. М., 1961.
Изображение каменотесов на египетском рельефе.
илл. 2
7.Мы используем обмерные данные, содержащиеся в одном из наиболее достоверных источников v I.E.S. Edwards. The Pyramids of Egypt. London, 1976.
Пирамиды Хеопса, Хефрена и Микерина. Схема соразмерностей.
8.Для характеристики гармонических качеств пирамиды отметим, что каждая ее треугольная грань имеет форму, близкую к равностороннему треугольнику (19 : 20), а диагональный разрез пирамиды имеет соотношение грани пирамиды к диагонали квадратного основания равным очень близко к 1 : 1,5 или 2 : 3.
9.Всеобщая история архитектуры. М., 1944, т. I, с. 88
илл. 3
10.M. Collignon.
11.Небольшая неточность -
?Квадратные» соразмерности
План Парфенона. Схема соразмерностей 1.
План Парфенона. Схема соразмерностей 2.
План Парфенона. Схема соразмерностей 3.
12.Н. И. Брунов. Пропорции античной и средневековой архитектуры. М., 1935.
Парфенон: ордер. Дорифор Поликлета: схема соразмерностей.
Пропилеи. Большой и малый ордер.
13.Колонны восточного портика Пропилей меньше колонн западного портика на величину плинта, на котором они установлены.
14.Архитекторы Филокл и Архилох лишь наблюдали за строительством, но, по-видимому, авторами проекта не были.
Эрехтейон. План.
15.Обмерные данные заимствованы из книги: J. Paton, The Erechteum.
Гермес Праксителя:
схема соразмерностей.
16.Н. И. Брунов. "Парфенон и Эрехтейон", М., 1973.
17.Цит. по сборнику: Архитектура античного мира. М., 1940, с.345.
Акрополь. План.
18.См. Н.И. Брунов. Пропорции в античной и средневековой архитектуре. М., 1935, с. 60
19.?Илиада», Песнь XXIII, строка 164
Пантеон. План.
20.Чертежи, план, разрез, фасад заимствованы из книги обмеров Дегоде "Les Edifices Antiques de Rome dessine s et me sure s exactement par Antoine Desgodetz Architecte. A Paris 1697». Несмотря на давнее издание, публикуемые в нем обмеры отличаются полной достоверностью и точностью.
21.Названия «греческий» и «римский» футы имеют условный характер, наличие этих мер можно проследить в классической Греции V века, и в Древнем Риме. Сотношение футов можно приравнять к 20 : 21, или сторонам целочисленного треугольника - 20, 21, 29.
Базилика Максенция
Базилика Максенция. Схема соразмерностей.
Храм Софии в Константинополе
Храм Софии в Константинополе. План.
22.E.Swift, Hagia Sophia. New York, 1940 p.159.
23.В
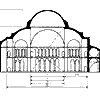
Храм Софии в Константинополе. Продольный разрез.
24.Древнегреческий фут
равен
25.Греческий текст этого
стихотворения, относящийся к 931-944 гг., был опубликован французскими
филологом Леграном и археологом Рейнахом (E. Legrand et F. Reinach. Description des oeuvres d' art et de
l' eglise des S. Apo tres de Constantinope par Constantin le Rhodien // Revue
des Etudes greques IX, 1896, p. 32-103.
26.См. подробнее: К. Н. Афанасьев. "Построение архитектурной формы древнерусскими зодчими". М., 1961, с. 209-210.
27.Десять книг об архитектуре Витрувия с комментариями Даниеле Барбаро. М., 1938, с. 29.
Храм Софии в Салониках. План
Храм Софии в Киеве. План.
Храм Софии в Киеве. Продольный разрез.
28.Подробно см.: К. Н. Афанасьев. "Проект реконструкции храма Софии в Новгороде". Приложение к книге "Построение архитектурной формы древнерусскими зодчими". М., 1961.
29.Сборник "Древнерусское искусство". М., 1977.
Храм Софии в Новгороде. План.
Храм Софии в Новгороде. Продольный разрез
30.Б. М. Полевой. "Искусство Греции”. М., «Искусство», в 3-х томах, 1970-75.
Все материалы библиотеки охраняются авторским правом и являются интеллектуальной собственностью их авторов.
Все материалы библиотеки получены из общедоступных источников либо непосредственно от их авторов.
Размещение материалов в библиотеке является их цитированием в целях обеспечения сохранности и доступности научной информации, а не перепечаткой либо воспроизведением в какой-либо иной форме.
Любое использование материалов библиотеки без ссылки на их авторов, источники и библиотеку запрещено.
Запрещено использование материалов библиотеки в коммерческих целях.
Учредитель и хранитель библиотеки «РусАрх»,
академик Российской академии художеств