РусАрх

 

Электронная научная библиотека

по истории древнерусской архитектуры

 

 

О БИБЛИОТЕКЕ

ИНФОРМАЦИЯ ДЛЯ АВТОРОВ

КОНТАКТЫ

НА ГЛАВНУЮ СТРАНИЦУ САЙТА

НА СТРАНИЦУ АВТОРА

 

 

Источник: Черепнин Л.В. Русская хронология. М., 1944. Все права сохранены.

Сканирование материала и размещение его электронной версии в открытом доступе произведено: www.russiancity.ru (Русский город. Архитектурно-краеведческая библиотека). Все права сохранены.
Размещение в библиотеке «РусАрх»: 2006 г.

 

 

Л.В. Черепнин

Русская хронология


 Предисловие

 

        Кафедра вспомогательных исторических дисциплин Историко-Архивного Института ГАУ НКВД СССР уже в первые годы своей работы поставила себе задачу подготовки пособий по предметам ее преподавания. Слабая разработка в предыдущие годы многих из вспомогательных исторических дисциплин и отсутствие специалистов по некоторым из них требовали нередко не только большой предварительной исследовательской работы, но и затрудняли подыскание компетентных авторов, которые могли бы взяться за подобные пособия. Все эти трудности удалось преодолеть в последнее время. В 194243 уч. году под руководством покойного заведующего кафедрой проф. А. Н. Сперанского, много сделавшего для организации педагогической и научной работы кафедры, было приступлено, наконец, к подготовке некоторых основных пособий: проф. Н. С. Чаев в Ленинграде уже к 1942 г. написал пособие по палеографии, которое А. Н. Сперанский предполагал дополнить и расширить. Все последние годы своей жизни А. Н. Сперанский (сконч. 9 января 1943 г.) много работал над пособием по дипломатике. Труды Н. С. Чаева и А. Н. Сперанского остались однако незаконченными. По поручению кафедры еще при жизни А. Н. Сперанского Л. В. Черепнин начал свои работы над пособиями по хронологии и метрологии, для которых использовал также работы Н. В. Устюгова.
        Приняв заведывание кафедрой после А. Н. Сперанского, я считал необходимым прежде всего продолжить работу кафедры по подготовке пособий и довести ее до определенного конца. На основании имевшихся предположений в начале 19431944 уч. года кафедрой был разработан план подготовки пособий в 1943-1945 гг.; этот план предусматривал не только окончание уже начатых работ по хронологии и метрологии, но также приготовление пособий по палеографии, дипломатике, которые должны составить части 1 и 2 пособий, а также но сфрагистике, геральдике, древне-русскому языку, исторической географии, историческому источниковедению и некоторым другим предметам. Работа была распределена прежде всего между членами кафедры: А. И. Андреевым, Е. А. Василевской, В. К. Лукомским, А. А. Новосельским и Л. В. Черепниным.
        Выполняя этот план, Л. В. Черепнин закончил начатые еще в 1942 г. работы по хронологии и метрологии, которые и являются первыми по времени выхода в свет пособиями, подготовляемыми кафедрой. В настоящее время Л. В. Черепнин подготовил также пособие по палеографии, в части своей написанное покойным проф. Н. С. Чаевым; Е. А. Василевская заканчивает первую

-7-

часть пособия по древне-русскому языку; А. И. Андреев занят подготовкой (пособия по дипломатике. В 1945 г. намечено подготовить пособие по сфрагистике (А. И. Андреев), геральдике (В. К. Лукомский), древненрусскому языку (ч. II, Е. А. Василевская) и др.
        Пособие по хронологии Л. В Черепнина вместе с приготовленным тем же автором пособием по метрологии основаны прежде всего на тех трудах по хронологии и метрологии, которые в небольшом количестве имеются в русской исторической литературе XVIII-XX вв. При неразработанности многих вопросов этих дисциплин, посвященных изучению старых единиц времени, веса, денежного счета и т. п., Л. В. Черепнину пришлось некоторые вопросы разработать заново, и его пособия являются не только обычными работами этого типа, подводящими итоги сделанного ранее, но также новыми исследованиями в области вопросов, неразрешенных до него; они несомненно помогут студентам в их работе, но привлекут также внимание специалистов-историков, которые найдут в них много нового и ценного по хронологии и метрологии.
        Главное Архивное Управление НКВД СССР, считая работу кафедры ио подготовке пособий одной из основных ее задач и всемерно содействуя этой работе, включило пособия, приготовляемые кафедрой в свой издательский план 1944-1945 гг. Изданием пособий по хронологии и метрологии Главное Архивное Управление начинает серию пособий по вспомогательным историческим дисциплинам.


Заведующий кафедрой вспомогательных
исторических дисциплин Историко-
Архивного Института ГАУ НКВД СССР
доктор исторических наук А. И. АНДРЕЕВ
28 октября 1944 г.

-8-

 I. ВВЕДЕНИЕ

 

         § 1. Предмет и задачи хронологии как вспомогательной исторической дисциплины. Термин "хронология" происходит от двух греческих слов: "хронос" - время и "логос" - слово, знание, учение. Таким образом, хронология - это наука об измерении времени.
        Наука эта распадается на два раздела: 1) хронологию математическую и 2) хронологию историческую (или, как её называют иначе, - техническую). Математическая хронология, ставит своей целью установление, при помощи соответственных вычислений, точного астрономического времени по движению небесных тел. Задачей исторической хронологии является определение, путём изучения дошедших до нас документальных данных, времени отдельных исторических событий. В этом разрезе (который и является предметом дальнейшего изложения), хронология должна заниматься научной разработкой имеющихся в исторических источниках дат (т. е. цифровых знаков, указывающих на время, к которому относится тот или иной исторический факт). Счёт времени у различных народов в различные периоды их прошлого не был одинаков, в силу чего в исторических источниках наблюдается необычайное разнообразие датировок. Для правильного понимания последних необходимо знакомство с системами времясчислений, применявшимися в разные эпохи разными народами, и умение перевести даты со старинного счёта на современный, выразив их в единообразных единицах измерения времени, принятых в наши дни.
        Хронология, таким образом, является важной вспомогательной исторической дисциплиной, т. к. размещение событий во времени (или, как принято говорить, в правильной хронологической последовательности) представляет необходимое условие научного изучения исторического прошлого. Это исчерпывающим образом вскрыто в постановлении Совнаркома СССР и ЦК ВКП(б) от 16 мая 1934 г.: "О преподавании гражданской истории в школах СССР". "Решающим условием, - говорится в этом постановлении, - прочного усвоения учащимися курса истории является соблюдение историко-хронологической последовательности в изложении исторических событий с обязательным закреплением в памяти учащихся важнейших исторических явлений, исторических деятелей, хронологических дат. Только такой курс истории мож,ет обеспечить необходимые для учащихся доступность, наглядность и конкретность исторического материала, на основе чего только и возможны правильный разбор и правильное обобщение исторических событий, подводящие учащегося к марксистскому пониманию истории"

-9-

        Хронологическими датами принято называть даты исторических событий не в том сыром виде, в каком мы извлекаем их из источников. Этот термин .применяется в отношении дат научно обработанных теми техническими средствами, которые даёт в руки историкам вспомогательная дисциплина - историческая, или техническая хронология.
        Историческая (техническая) хронология разрабатывает методы научного анализа источников на основе тех данных, которыми располагает хронология математическая, т. к. различные системы измерения времени находятся в тесной связи с наблюдениями над природными (астрономическими) явлениями. В этом отношении историк должен работать рука-об-руку с математиком-астрономом, используя в своих целях выводы последнего.
         § 2. Астрономические явления как основа времясчисления. Любая хронологическая система должна, во-первых, выработать единообразные, твёрдые и точные единицы для измерения времени, а во-вторых, остановиться на какой-то отправной, исходной точке, от которой бы и начинался счёт.
        Путь к разрешению первой задачи подсказывала сама природа. Не трудно заметить, что в ряде астрономических явлений наблюдается закономерная повторяемость. Достаточно указать на периодическую смену дня и ночи, лунных фаз, времён год и т. д. Эта строгая периодичность в жизни природы, зависящая от движения небесных тел, была давно вскрыта людьми и положена ими в основу измерения времени. Уже на ранних ступенях исторического развития хозяйственные потребности отдельных народов выдвигали настоятельную нужду в применении астрономических данных к счёту времени. Энгельс отметил в "Диалектике природы", что "...астрономия - уже из-за времён года абсолютно необходима для пастушеских и земледельческих народов" (Маркс и Энгельс, Соч., т. XIV, стр. 438).
        Если мы присмотримся к тем основным единицам счёта времени, которыми пользуется большинство современных культурных народов, т. е. к суткам, месяцу и году, то легко убедимся, что эти три единицы определяются тремя астрономическими факторами: вращением земли вокруг своей оси, обращением луны вокруг земли и движением земли вокруг солнца. Средний период времени, в течение которого земля совершает полный оборот вокруг своей оси, составляет до 24 часов и носит в астрономии название солнечных суток. Период.наблюдаемого нами чередования лунных фаз (т. е. новолуния, первой четверти, полнолуния и последней четверти), зависящий от движения луны вокруг земли, астрономы называют синодическим месяцем. Его длина =29,5306 суток или 29 суток 12 часов 44 минуты 3 секунды. Слово месяц имеет таким образом двойное значение. Им одновременно обозначается и луна, и единица времени, определяющаяся периодическими перемещениями этого небесного тела. Это очень показательно для отмеченной выше непосредственной связи между астрономическими явлениями и времясчислением. Термин "синодический" происходит от греческого слова, означающего схождение. Промежуток времени

-10-

между двумя новолуниями получил название синодического месяца потому, что луна, обращаясь вокруг земли, приходит в различные положения относительно солнца и в конце указанного периода как будто сходится с ним. Время обращения земли вокруг солнца в астрономической науке принято называть солнечным или тропическим годом. Его продолжительность составляет величину, равную 365,2422 средних суток = 365 суткам 5 часам 48 минутам и 46 секундам. У различных народов начало года приходится в разное время. Для вычисления длины тропического года астрономы берут за основу постоянную величину - весеннее равноденствие, т. е. время, когда продолжительность дня и ночи является одинаковой.
         § 3. Виды календарей. Система времясчисления, строющаяся на определённом, точно установленном взаимоотношении отдельных единиц измерения в виде года, месяца, суток, называется календарём. Последний термин происходит от латинского слова "календы", которым в древнем Риме обозначалось первое число каждого месяца.
        Среди многочисленных различных календарных систем можно наметить два основных типа: 1) солнечные календари, астрономическую основу которых составляет тропический год или период годичного обращения земли вокруг солнца и 2) календари лунные, возникшие на основе синодического месяца или законченного периода чередования лунных фаз.
        Трудность построения календаря любого из двух названных типов заключается в том, что ни тропический год, ни синодический месяц не заключают в себе полного количества суток. Поэтому при установлении продолжительности календарных года и месяца приходится отступать от точных астрономических данных. Отсюда возникают понятия "тропический год" и "календарный год", "синодический месяц" и "календарный месяц".
         § 4. Солнечные календари. Египетский календарь. Солнечный календарь обычно исходит из равенства года или 365 или 366 суткам, округляя таким образом астрономически установленную величину - 365,2422 суток. История знает две основных разновидности солнечного календаря: 1) так называемую "блуждающую" календарную систему и 2) систему високоса. Блуждающий солнечный календарь зародился в очень давние времена, в древнем Египте. Египтяне принимали продолжительность календарного года за 365 суток, т. е. почти на целую четверть суток менее длины тропического года (=365,2422 суток - 365 суток = почти 0,25 суток). В результате такого отступления от астрономических данных, начало египетского года, меньшего по величине, чем тропический, постепенно и медленно передвигалось в пределах последнего, падая на различные сезоны (лето, осень, зиму, весну). Отсюда позднейшее название египетского календаря "блуждающим". Наблюдая за этим "блужданием", нетрудно убедиться, что при расхождении между египетским календарём и тропическим годом на величину около четверти суток, через каждые 1460 лет начало египетского календаря возвращалось к одному и тому же моменту солнечного года (4 х 365 = 1460). Этот промежуток в 1460 лет получил назва-

-11-

ние "периода Сотиса". "Сотис" - греческое наименование звезды Сириуса. Своё летосчисление египтяне связывали с наблюдениями за движением Сириуса, положение которого на небе менялось в связи с годичным обращением земли вокруг солнца и восход которого раз в 1460 лет совпадал с разливом реки Нила.
        Из народов СССР египетскую календарную систему применяли армяне, о чём будет сказано в специальном разделе, посвященном древне-армянской хронологии.
         § 5. Юлианский календарь. Неудобство "блуждающего" календаря вызвало современем переход к так называемой системе високоса. Её смысл заключается в том, что в качестве средней лродолжительности календарного года берётся величина в 365,25 суток, почти равная длине тропического года (365,2422 суток). Но поскольку неудобно считать в году неполное количество суток, постольку указанная система строится на чередовании простых годов (в 365 суток) и удлиннёиных, с одним добавочным днём (в 366 суток).
        Введение в жизнь подобного календаря связано с именем знаменитого римского государственного деятеля Юлия Цезаря, осуществившего это начинание при участии египетского астронома Созигена в 46 г. до н. э. Нам нет надобности останавливаться на структуре древне-римского календаря, предшествовавшего реформе Цезаря. Достаточно отметить основной принцип этой реформы: на каждое четырёхлетие приходится три года простых (по 365 суток) и один удлинённый или високосный (в 366 суток). При таком построении календаря средняя продолжительность года (365,25 суток) оказывается весьма близкой к астрономическим данным (365,2422 суток). Самое название "високос", "високосный" происходит от латинского слова "биссекстум", т. е. "второй шестой". Дело в том, что добавочным днём для удлиннённого года в римском календаре было второе 24 февраля. Римляне, как было указано выше, вели счёт календами (название первого числа каждого месяца), но не вперёд, а назад. Поскольку в феврале было 28 дней, постольку 23 февраля являлось шестым днём до мартовских календ (до 1-го марта). А добавочный день после 23 марта получил название двойного шестого ("биссекстум" - "високос"). Отсюда самый год с одним дополнительным днём в феврале стал называться, в отличие от простого, високосным. В нашем современном календаре, ведущем своё происхождение от римского, добавочным днём в високосном году является 29 февраля. Февраль простого года имеет 28 дней, февраль високосного - 29 дней. Остальные месяцы, как в простом, так и високосном, году насчитывают или по 30 дней (апрель, июнь, сентябрь, ноябрь), или по 31 (январь, март, май, июль, август, октябрь, декабрь). Тем, кто затруднится запомнить количество дней в каждом месяце, рекомендуется для счёта дней в отдельных месяцах пользоваться косточками пальцев на руках и промежутками между ними. Располагая месяцы в порядке их следования в пределах года, надо иметь в виду, что.те из них, которые лридутся на косточки, будут содержать по 31 дню, те .же, которые

-12-

окажутся между двумя косточками, - по 30 дней (за исключением февраля).
        Для того, чтобы определить по цифровому обозначению года, является ли он простым или високосным, следует руководствоваться признаками делимости числа на 4, т. к. високосным является каждый четвёртый год. Поэтому, если две последних цифры числа, обозначающего год, делятся на 4, или же если это число оканчивается двумя нулями, следовательно, год - високосный. Во всех других случаях год - простой. Например, и 1600 и 1820 годы будут високосными, т. к. первое число оканчивается двумя нулями, а второе цифрой 20, делящейся на четыре. Но 1943-й год - простой, т. к. 43 на четыре не делится.
        Юлианский календарь лёг в основу календарной системы, которой пользуется в настоящее время большинство культурных стгран, и в частности и СССР, но не в чистом виде. В XVI в. этот календарь подвергся дальнейшей реформе, задачи и характер которых будут вскрыты ниже.
         § 6. Григорианский календарь. Юлианский календарь, конечно, являлся шагом вперёд по сравнению с египетским, т. к. он гораздо удачнее разрешал проблему приближения средней продолжительности года к величине, установленной астрономическими вычислениями. Однако, этот календарь ещё не был совершенным. Если египетский год был короче тропического, то Юлианский оказывался, наоборот, несколько длиннее последнего. Юлианский календарный год, хоть и незаметно, но систематически отставал от тропического года. Это, на первый взгляд как будто совершенно незначительное отставание (365,25 - 365,2422 суток) достигало целых суток в течение каждых 128 лет, а к концу XVI в. дошло уже до 16 суток (т. к. Юлианский календарь был принят к употреблению в христианских странах на соборе в Никее в 325 г., т. е. в начале IV в.). Встал вопрос о новой реформе календаря, которая и была осуществлена в 1582 г. особой комиссией, созданной римским папой Григорием XIII. Эта реформа преследовала правда не столько научные цели, сколько задачи церковного характера, связанные с определением дня празднования пасхи. Но её результаты имели вполне научное значение
        Перед комиссией, возглавляемой папой Григорием XIII, стояли две основных задачи: 1) ликвидировать каким-либо способом разницу в 10 суток между тропическим и календарным годом, накопившуюся за прежние столетия; 2) путём соответствующих изменений в структуре Юлианского календаря, устранить, или во всяком случае уменьшить, эту разницу на будущее время.
        Первая задача была разрешена чисто административным порядком. Соответствующим папским декретом было предписано 5 октября 1582 г. считать 15-м октября. Таким образом, текущий 1582 год был укорочен на 10 суток и этим было восстановлено нарушенное соответствие, несколько отставшего в прошлом Юлианского календаря, тропическому году.
        В целях дальнейшего приближения календарного года к тропическому, комиссия пошла по естественному пути сокращения

-13-

количества високосных годов. Действительно, принимая каждый четвёртый год за високосный, Юлианский календарь исходил из предпосылки о средней продолжительности года в 365,25 суток. Но ведь эта средняя величина несколько превышает астрономические данные (год = 395, 2422 суток). Если основываться на последних, то уже не каждый четвёртый год придётся считать за високосный. Григорианская реформа и исключила в пределах каждого 400-летия три високосных года. Это сокращение конкретно коснулось некоторых из тех годов, которые завершают столетия, или другими словами, цифровое обозначение которых оканчивается двумя нулями. Чтобы наглядно представить себе, в чём дело, возьмём за исходную точку 1582 год - момент реформы. Выпишем те годы (после 1582 г.), которыми заканчиваются четыре последовательных столетия. Это:
        1600 г. (грань между XVI и XVII вв.)
        1700 г. (грань между XVII и XVIIl вв.)
        1800 г. (грань между XVIII и XIX вв.)
        1900: г. (грань между XIX и XX вв.).
        Все эти годы, по Юлианскому календарю, являются високосными, т. к. обозначающие их цифры заканчиваются двумя нулями. Григорианская комиссия предложила считать из этих лет за високосные только те, у которых две первых цифры делятся на 4. Следовательно, по Григорианскому календарю високосным будет только 1600 г. (т. к. цифра 16 делится на 4). Остальные три года относятся к числу простых, т. к. ни 17, ни 18, ни 19 на четыре не делятся.
        Надо твёрдо усвоить, что это нововведение, связанное с именем папы Григория XIII, касалось исключительно только тех годов, которые отделяли друг от .друга соседние столетия и обозначались цифрами с двумя нулями на конце. Григорианская реформа отнюдь не затрагивала тех годов, которые находились внутри, столетия. Для распределения их на простые; и високосные оставалось в силе старое правило, .которому подчинялся Юлианский календарь, т. е. признаки делимости на четыре. Скажем, признав 1700 год (как заканчивающий век) простым, в силу того, что его две первых цифры не делятся на четыре, Григорианская комиссия вовсе не устанавливала, что и все дальнейшие годы, следующие за 1700-м (именно 1701, 1702, 1703, 1704 и т. д.), по той же самой причине будут простыми. Для выявления високосных лет в этих случаях, как и в Юлианском календаре, имели значение не первые две цифры, а наоборот, две последние. Так 1701 год, - простой, т. к. число 01 на четыре не:делится, а 1704-й - високосный (несмотря на то, что 17 не делится на четыре), в силу того, что 04 на четыре делится. Но как только дело доходит до очередного года на грани двух столетий (скажем, 1800), так решающим признаком для отнесения его к разряду простых или високосных является делимость на четыре двух первых цифр.
        Словом, в Григорианском календаре каждый период в 400 лет; имеет на три високосных года меньше, чем в Юлианском. В силу этого средняя продолжительность Григорианского календарного

-14-

года меньше, чем Юлианского; Григорианский календарь совершеннее, чем Юлианский. Расхождение между Григорианским календарным годом и тропическим на одни сутки наступает уже не в 128 лет (как в Юлианском календаре), а в 3500 лет.
        Григорианский календарь был принят в различных странах в разное время. В России он был введен только после Октябрьской революции, на основании декрета Совнаркома, с 14 февраля 1918 г.
         § 7. Взаимоотношение Юлианского и Григорианского календарей ("старого" и "нового" стилей). Одновременное существование в различных странах двух календарных систем вылилось в разницу двух "стилей": "старого" (Юлианский календарный счёт) и "нового" (Григорианский календарный счёт).
        В России, до Октябрьской революции господствовал "старый стиль". В 1918 г., как указано, наша страна перешла на "новый стиль". Мы привыкли считать, что "старый стиль" отстаёт от "нового" на 13 суток. Скажем, 15 апреля 1943г. по "новому стилю" соответствует 2 апреля 1943 г. по "старому стилю". Но не все отдают себе отчёт, откуда происходит эта разница на 13 суток между двумя календарными "стилями". Не умея объяснить этого обстоятельства, многие впадают в грубую ошибку, когда желая выразить, по "новому стилю" некоторые даты прошлых столетий (ХIХ-го, XVIII-ro и более ранних), не долго думая, увеличивают их на 13 суток.
        Чтобы уяснить себе в чём состоит эта распространённая ошибка, мы должны вернуться к тому моменту, начиная с которого ведет своё существование Григорианский календарь, - к реформе 1582 г. Реформа Юлианского календаря была вызвана, как мы знаем, тем, что последний отстал от тропического года на 10 суток. Декрет папы Григория XIII ликвидировал эту разницу. Следовательно, те страны, которые перешли на Григорианский календарный ("новый") стиль, стали считать на 10 суток вперёд. Те страны, которые сохранили Юлианский календарь ("старый стиль"), отставали в своём счёте на 10 суток.
        Эта разница, на 10 суток между "старым" и "новым" стилями, сложившаяся к XVI в., не могла оставаться постоянной. Ведь Григорианский календарь насчитывает меньше високосных годов, чем Юлианский. Следовательно, рано или поздно должен был наступить такой год, который будучи високосным (=366 суток) по Юлианскому календарю, по Григорианскому был бы простым (=365 суток). Тогда расхождение между двумя "стилями" вылилось бы уже в 11 суток (на одни сутки больше). Когда же наступит этот момент? Ясно, что решающим может быть только один из годов, оканчивающих век (1600-й, 1700-й, 1800-й, 1900-й и т. д.), т. к. для всех других годов в пределах столетий распределение на високосные и простые остаётся одинаковым и по Юлианскому, и по Григорианскому календарному счёту.
        Рассмотрим же по очереди все годы, завершающие столетия (с XVI по XIX). 1600 год (являющийся гранью между XVI и XVII вв.) будет високосным и по Юлианскому календарю (т. к. цифровое обозначение его оканчивается двумя нулями), и по Гри-

-15-

горианскому (т. к. две его первых цифры делятся на четыре). Следовательно, в XVII столетии разница между "старым" и "новым" стилями не увеличится, оставаясь равной полрежнему 10 суткам.
        1700 год (грань между XVII и XVIII вв.) - високосный (= 366 суткам) по Юлианскому календарю (т. к. цифровое обозначение его оканчивается двумя нулями) и простой (= 365 суткам) по Григорианскому (т. к. две его первых цифры -17 - не делятся на четыре). Следовательно, в XVIII в. разница между двумя "стилями" возрастёт уже до 11 суток (на сутки больше).
        В XIX в. эта разница доходит до 12 суток (1800 год, на основания указанных выше признаков, является високосным по Юлианскому календарному счёту и простым - по Григорианскому счёту). И, наконец, в XX в. расхождение "стилей" достигает 13 суток (1900 год - високосный по Юлианскому календарю, простой по Григорианскому).
        Вот чем объясняется это несовпадение на 13 суток между "старым" и "новым" стилями, которое установилось к XX столетию. И вот почему нельзя исходить из этой цифры - 13 при переводе на "новый стиль" дат прошлых столетий. Надо усвоить себе следующее правило, к которому привели нас все предшествующие рассуждения: для перевода на "новый стиль" дат XVI-XVII вв. следует их увеличить на 10 суток, даты XVIII в. при переводе увеличиваются на 11 суток, даты XIX в. - на 12 суток, даты XX в. - на 13 суток. Поэтому 15 октября 1586 г., "старого стиля" соответствует 25 октября 1586 г. "нового стиля". 17 июля 1643г. "старого стиля" = 27 июля 1643 г. "нового стиля". 21 мая 1741 г. "старого стиля" - 1 июня 1741 г. "нового стиля". 15 апреля 1833 г. "старого стиля" = 27 апреля 1833 г., "нового стиля". 18 августа 1901 г. "старого стиля" = 31 августа 1901 г. "нового стиля".
        He ограничиваясь историей взаимоотношения Юлианского и Григорианского календарей в прошлом, мы можем заглянуть в будущее и поинтересоваться, когда наступит момент дальнейшего расхождения "старого" и "нового" стилей. Очевидно, не в ХХI столетии, т. к. находящийся на грани - XX и XXI веков 2000 год будет високосным и по Юлианскому и по Григорианскому счёту (число 2000 оканчивается двумя нулями, а 20 делится на 4). Таким образом, на 14 суток Григорианский календарь обгонит Юлианский только в XXII в.
        Помимо Юлианской и Григорианской календарных систем, история знает и другие попытки создания солнечного календаря на основе, по возможности, максимального приближения к средней продолжительности тропического года. Таков, например, опыт Великой Французской буржуазной революции, во время которой в 1793 г. был создан своеобразный революционный календарь. Он не устанавливал никакой постоянной системы високоса. Его начало совпадало с моментом осеннего равноденствия (временем равенства дня и ночи) и определялось каждый раз специальными астрономическими вычислениями.
        Можно отметить также Ново-Юлианскую календарную систему,

-16-

разработанную в 1923 г. в связи с переходом Балканских стран на "новый стиль". Её задачей являлось, путём соответствующего распределения простых и високосных лет, ещё более уточнить (по сравнению с Григорианским календарём) соответствие календарного года тропическому.
        Мы не будем останавливаться подробно на всех разновидностях солнечного календаря, выработанных различными народами в различные эпохи. Для понимания русской хронологии достаточно хорошо представить себе соотношение календарей: Юлианского, бывшего в употреблении до Октябрьской революции, и Григорианского, вошедшего в обиход с 1918 г.
         § 8. Лунные календари. Сказанное выше относится к русской хронологии. Но многие нерусские национальности, входящие в состав Советского Союза, пользовались в прошлом (а некоторые пользуются и теперь) различными системами лунного календарного счёта. Поэтому коротко необходимо остановиться и на последнем. Его основная задача - добиться чтобы начало каждого месяца приходилось всегда на одни и те же фазы луны. Если солнечный календарь исходит, в качестве постоянной величины, из периода обращения земли вокруг солнца, определяющего чередование времён года, то лунный календарь берёт за исходную величину продолжительность синодического месяца, т. е. законченного периода смены лунных фаз.
        Известны две основных разновидности лунных календарных систем. Первая получила распространение в мусульманских странах. В её основу положен год, состоящий из 12 календарных лунных месяцев, при чём продолжительность каждого из них (в среднем 29,5 суток) приблизительно равна длине синодического лунного месяца (29,5306 суток). Поскольку календарный месяц не может заключать в себе неполного количества суток (29,5), обычно принята система чередования пустых и полных лунных месяцев(т. е. календарных месяцев по 29 и 30 суток). Таким образом, длительность календарного лунного года выражается в 354 сутках (29,5 суток х 12). Благодаря тому, что средний календарный лунный месяц (=29,5 суток) несколько короче месяца синодического (=29,5306 суток), с течением времени нарушалось соответствие начального числа каждого месяца определённым лунным фазам. Для восстановления утраченного равновесия было необходимо в пределах какого-то, соответственным образом рассчитанного, цикла лет, наряду с простыми годами (по 354 суток), вставить некоторое количество удлинённых (високосных) годов (по 355 суток). Таким путём в какой-то мере парализовалось отставание синодического месяца от календарного.
        Лунный календарный год, складывающийся из 354-355 суток, носит название свободного или блуждающего, т. к. он не находится ни в какой связи с годом тропическим (солнечным). Его начало ежегодно перемещается (блуждает) по различным числам в пределах солнечного календаря.
        Календарные системы другого типа, именуемые обычно связанными или лунно-солнечными, ставили своей задачей установить со-

-17-

ответствие между двумя величинами: продолжительностью солнечного тропического года (= 365,2422 суток) и лунного месяца (=29,5306 суток).
        Солнечный год не содержит в себе полного количества лунных месяцев. Поэтому указанное выше соответствие может быть достигнуто только при условии, если какой-то (строго рассчитанный), период будет заключать в себе определённое количество календарных лет продолжительностью в 12 лунных месяцев и некоторое число лет, имеющих по 13 лунных месяцев. (Частное от деления 365,2422 на 29,5306 будет больше 12, но меньше 13). Задача построения лунно-солнечного календаря была разрешена монголами.
        Ниже, при изучении систем летосчислений народов СССР мы столкнёмся и детально познакомимся с обеими указанными календарными системами: свободной лунной (мусульманской) и связанной лунно-солнечной (тюрко-монгольской).
         § 9. Эры. Для того, чтобы ориентироваться в хронологических данных, далеко не достаточно одного знакомства с разными видами календарей, применявшимися в прошлом различными народами. Необходимо знать также эры этих народов, т. е. системы счёта лет от того или иного исходного момента. Ведь совершенно очевидно, что какой-бы календарный год ни имелся в виду, солнечный или лунный, блуждающий или високосный, - этот год, независимо от своей продолжительности, должен иметь какой-то порядковый номер. Он должен быть таким-то по счёту от какой-то даты, принятой за основу летосчисления. Самый термин "эра", как предполагают, складывается из четырёх начальных букв отдельных слов следующей фразы: "ab exordio regni Augusti", т. е. "от начала царствования Августа" (aera - эра). Такое происхождение слова объясняется тем, что в ряду различных систем летосчисления, употреблявшихся в прошлом, одно время пользовалась распространением "эра Августа" (в Александрии).
        В основе эр различных народов часто лежат даты каких-либо событий, имевших в своё время политическое значение, например, начальные даты правления царей или высших должностных лиц и т. д. Но эры отнюдь не обязательно должны носить реальный характер. Большим распространением пользовались также фиктивные эры, за исходный пункт которых принимались явно вымышленные мифические события, например, "сотворение мира" или основание Рима, год которого в действительности не известен. Фиктивный характер эры отнюдь не мешает точности датировки событий, реально имевших место в истории. Ведь для правильности счёта важно лишь соблюдение точности для тех промежутков времени, которые отделяют друг от друга подлежащие датировке факты. Но абсолютно не имеет значения достоверность или же вымышленность исходной точки, от которой ведётся счёт.
        При изучении русской хронологии следует обратить внимание на две эры (обе фиктивные): от "сотворения мира" и от "рождества христова". Первая система летосчисления была принята в Византии, оттуда перешла в Россию (после принятия последней

-18-

христианства) и (применялась в русских источниках до 1700 г. С этого времени Россия перешла на христианскую эру.
        Христианская эра, или система летосчисления от "рождества христова" была создана искусственно римским монахом Дионисием Малым в VI в. н .э. В его время была в ходу так называемая "эра Диоклетиана", т. е. счёт лет вёлся от даты вступления на престол римского императора Диоклетиана. Путём разных фантастических вычислений года рождения Христа, Дионисий отнёс это мифическое событие ко времени за 284 года до начала эры Диоклетиана, или другими словами, приравнял начальный год царствования последнего к 284 г. христианской эры.
        Эра Дионисия принята в настоящее время большинством культурных народов. В России она вошла в употребление, как указано, с Петра I.
         § 10. Задачи конкордации и редукции хронологических дат. Разнообразие систем датировок, с которыми сталкивается исследователь при изучении исторических источников различных времён и народов, выдвигает необходимость их согласования. Поэтому хронология, как вспомогательная историческая дисциплина, ставит перед собою две задачи: 1) конкордации и 2) редукции хронологических дат.
        Конкордация дат состоит в установлении взаимоотношения между различными системами летосчисления (календарями и эрами). Редукция заключается в выработке принципов перевода дат с одной хронологической системы на другую (с учётом разницы в календарном счёте и эре).
        В дальнейшем предметом нашего рассмотрения будет древнерусская хронология и хронологические системы различных народов СССР. Мы должны будем указать на принципы конкордации и ознакомиться с методами редукции дат, встречающихся в источниках по истории древней Руси и народов СССР, - на эру от "рождества христова".

 II. ДРЕВНЕ-РУССКАЯ ХРОНОЛОГИЯ

         § 1. Древне-русское обозначение цифр. Прежде чем говорить о характере древне-русских хронологических систем, необходимо познакомиться с древне-русским обозначением цифр, отличающимся от современного. Ведь совершенно очевидно, что для того, чтобы переводить даты со старинного летосчисления на нашу эру, надо предварительно ещё научиться их читать.
        Принятое в настоящее время большинством культурных народов так называемое арабское обозначение чисел, построенное на различных комбинациях девяти цифр с нулём, в России вошло в обиход только в начале XVIII в. В до-Петровской же Руси применялась цифровая система, заимствованная из Византии. Эта система не знала нуля, в силу чего особые знаки требовались не только для единиц, но и для десятков и сотен. Такими знаками служили соответственные буквы алфавита: в Византии - греческого, в России - славянского. А так как славянский алфавит возник под зна-

-19-

чительным воздействием греческого, то совершенно естественно, что и числовое значение отдельных русских букв было установлено по византийскому образцу. Таким образом, каждая буква выполняла двойную роль: знака, служащего с одной стороны - для словообразования, с другой - для указания определённого числа. Чтобы выделить буквы в этой последней роли, в значении цифр, над ними ставился особый значёк ~ (титло). Например:

_

А=1 1)

        Первым десяти цифрам соответствовали следующие буквы славянского алфавита: 2)

        __

        1 - А

   (аз)

        __

 

        2 - В

   (веди)

        __

 

        3 - Г

   (глаголь)

        __

 

        4 - Д

   (добро)

        __

 

        5 - Е

   (есть)

        __

 

        6 - S

   (зело)

        __

 

        7 - З

   (земля)

        __

 

        8 - И

   (иже)

        __

 

        9 -

   (фита)

        _

 

        10 - i

   (и десятиричное)


        Мы видим прежде всего, что при обозначении чисел буквами сохраняется последовательность алфfвита; но с некоторыми исключениями: так почему-то пропущены "б" и "ж". С другой стороны, "", занимающая последнее место в. славянской азбуке, перешла в данном случае на девятое место. Причины этих, на первый взгляд непонятных отступлений от основного принципа построения системы чисел, станут ясными, если мы обратимся к греческому прообразу славянской азбуки. В греческом алфавите отсутствуют специальные буквы "б" и "ж", поэтому они не имеют числового значения и в русской письменности. В то же время буква "фита" в греческом алфавите следует непосредственно за "и", - это же место она сохраняет и в древне-русском числовом ряду. Следует отметить наличие двух букв, и по гречески, и по славянски обозначавших звук "з". Им соответствуют две отдельных цифры. То же надо сказать и относительно звука "и". Для письменного его выражения существуют две буквы. Соответственно их числовому значению (восемь и десять), они называются: "и восьмеричное" и "и десятиричное".
        Для обозначения числительных от 11 до 19 включительно служат буквы, принятые для соответствующих единиц (1-9) в сочетании с буквой-цифрой:

_

i - 10

При этом единицы обязательно занимают первое место, десяток - второе:
        ___________
        1) В дальнейшем титло условно обозначается чёрточкой над буквой.
        2) В виду отсутствия типографских знаков для обозначения древне-русских букв, последние даются в современном начертании.

-20-

        __

        11 - аi

        __

        12 - вi

        __

        13 - гi

        __

        14 - дi

        __

        15 - еi

        __

        16 - si

        __

        17 - зi

        __

        18 - иi

        __

        19 - i


        Такой порядок расстановки цифр вполне отвечает, нашему произношению. Мы говорим: одиннадцать, двенадцать, тринадцать, т. е. - один, два, три на десять (сначала - единицы, потом - десяток).
        Десятки от 20 до 90 включительно обозначаются буквами славянской азбуки, следующими зa "i" (десять), при чём замечающееся в некоторых случаях нарушение строго алфавитной последовательности объясняется, как мы отмечали это и ранее, влиянием особенностей греческого алфавита.

        __

        20 - к

   (како)

        __

 

        30 - л

   (люди)

        __

 

        40 - м

   (мыслете)

        __

 

        50 - н

   (наш)

        __

 

        60 -

   (дифтонг "кси", т. е. знак, обозначающий два звука: "к" и "с"; в современном алфавите отсутствует)

        __

 

        70 - о

   (он)

        __

 

        80 - п

   (покой)

        __

 

        90 - ч

   (червь)


        Сочетание десятков, в пределах 20-90, с единицами происходит в порядке, обратном тому, который мы могли наблюдать для числительных 11 - 19. Именно, в числовом ряду десятки предшествуют единицам: Например:

        ___

        23 - кг

        ___

        35 - ле

        ___

        41 - ма

        ___

        58 - ни

        ___

        74 - од

        ___

        97 - чз

   и т. д.


        Подобное расположение цифр опять-таки подчиняется нашему произношению. Мы говорим - тринадцать, т. е. три на "дцать" (десять): ранее называем единицы. Но в то же время: тридцать пять, т. е. сначала произносим десятки.

-21-

        Для обозначения сотен берутся следующие буквы алфавита по порядку. Некоторое незначительное отступление от этого принципа не должно нас смущать, т. к. мы с ним сталкивались уже ранее и его причины нам понятны. Это - отражение греческой структуры алфавита, с которым славянский имеет некоторые расхождения.

        __

        100 - р

   (рцы)

        __

 

        200 - с

   (слово)

        __

 

        300 - т

   (твердо)

        __

 

        400 - у

   (ук)

        __

 

        500 - ф

   (ферт)

        __

 

        600 - х

   (хер)

        __

 

        700 -

   (дифтонг "пси", т. е. знак обозначающий два звука: "п" и "с"; в современной азбуке отсутствует)

        __

 

        800 -

   (дифтонг "от": большое "О" - греческая "омега" и над ней маленькая буква "т")

        __

 

        900 - ц

 


        В сочетании с десятками и единицами сотни всегда стояли на первом месте, а десятки и единицы располагались по указанным выше правилам.
        Например:

        ____

        125 - рке

        ___

        319 - тi

        _____

        684 - хпд

        ___

        913 - цгi


        Для обозначения тысяч особых букв не существовало. В этих целях использовались буквенные выражения тех цифр, которые указывали на количество тысяч. Для того, чтобы показать, что имеются в виду именно тысячи, к соответствующим буквам - цифрам присоединяется слева внизу особый значёк. Например:

        __

        1 000 - ‡а

        __

        2 000 - ‡в

        __

        3 000 - ‡г

        __

        5 000 - ‡е

        _

        10 000 - ‡i

        __

        20 000 - ‡к

        __

        50 000 - ‡н

-22-

        __

        100 000 - ‡р

        __

        500 000 - ‡ф


        При этом надо учитывать, что если количество тысяч не могло быть выражено одной буквой, то соответствующий тысячам значёк обязательно сопровождал каждую из букв, участвовавших в обозначении количества тысяч. При несоблюдении этого условия буквенное выражение приобретало другое числовое значение. Например:

            _________

        ‡ф‡м‡в - 542 000

            ______

        ‡фмв - 500 042

            _______

        ‡ф‡мв - 540 002


        В первом примере все три буквы указывают на количество тысяч, в остальных - только одна или две цифры, а остальные сохраняют своё обычное значение десятков и единиц.
        В некоторых рукописях приводятся особые сокращенные обозначения для крупных чисел (10000 и выше), но нам нет надобности на этом подробно останавливаться. Наша задача ограничивается приобретением навыков для прочтения дат, а самые большие цифровые выражения дат по древне-русской системе летосчисления укладываются в пределы семи тысяч.
        Как уже было указано, над буквами, имеющими цифровое значение, обычно ставилось особые значки (титла). Большею частью над единицами и десятками ставилось одно титло, над сотнями и тысячами в отдельности по титлу. Например:

__

 __

 ____

‡В

Р

КВ

   (2122)

Иногда встречается общий значок над всем числом:

__________

‡ГСМД

   (3244)

Наконец, в документах часто попадаются и различные другие варианты: титла над каждым буквенным знаком, употреблявшимся в значении цифр, в том числе и над десятками и единицами в, отдельности

__

 __

 __

 __

(‡Д

Т

М

В

   - 4342);

титла над одними тысячами, или над тысячами и сотнями, причём десятки и единицы остаются без значков над ними

__

 _____

(‡З

МВ

   - 7042)

и т. д.
        Иногда буквы в значении цифр сопровождались с обеих сторон точками, однако, десятки и единицы при этом обычно не отделялись друг от друга при посредстве точек. Но и это не являлось постоянным правилом. Мы можем встретить несколько различных вариантов буквенного обозначения одного и того же числа: точки или выделяют каждую цифру - букву, или отсутствуют совершенно, или же, наконец, сопровождают не все цифры, а только некоторые из них, например, десятки и единицы остаются не разделёнными. Так число 3042 может быть обозначено буквами следующим образом:

__ 

__  

__  

__ 

__ 

__ 

__ 

__ 

__ 

или ‡Г.

М.

В.

или ‡Г.

М

В

или ‡Г

М

В.

Знакомство с древне-русской цифирью очень важно, т. к. оно даёт возможность

-23-

историку прочесть даты имеющиеся в документах до XVIII столетия, когда в России вошло в употребление арабское обозначение цифр.
         § 2. Римские цифры. Говорить об арабском обозначении цифр нет надобности, т. к. оно общеизвестно. Но необходимо ознакомиться с так называемыми римскими или латинскими цифрами, бывшими в употреблении в древнем Риме и часто встречающимися в русских документах более позднего времени. Для цифр первого десятка были приняты следующие знаки: I-1, V - 5, X-10. Остальные цифры в пределах первого десятка обозначались теми же тремя знаками в сочетании с (единицей). Поставленная слева, цифра I уменьшала число на одну единицу, будучи помещена cnpaва, соответственно увеличивала его. Так получались цифры: II - 2, III -3, IV -4, VI -6, VII -7, VIII -8, IX -9.
        Как видим, каждый из знаков (V, X) использовался для образования чисел пять раз. Помимо того, что он обозначал определённую цифру, его комбинации с I давали одно число на единицу меньше данного и три числа - на единицу превышающие данное. Та же система применялась и для цифрового обозначения десятков. Они получались из аналогичных комбинаций двух цифр: L (50) и C (centum - 100) - с одной .стороны, и X (10) - с другой. Таким образом, Х=10, XX = 20 , XXX = 30, XL =40, L = 50, LX = 60, LXX = 70, LXXX = 80, XC = 90, С =100.
        В двузначных числах вначале указывались десятки, затем единицы. Например: 79 = LXXIX, 94 = XCIV, 58 = LVIII.
        При обозначении сотен фигурируют комбинации цифр: С (100), D (500) и М (mille -1 000). Система остаётся та же, какая принята для единиц и десятков. Поэтому: С=100, СС=200, ССС=300, СD=400, D = 500, DC = 600, DCC = 700, DCCC = 800, DCCCC = 900, M=1000.
        В трёхзначных числах последовательно идут сотни, десятки, единицы. Например: 348 = CCCXLVIII, 724 = DCCXXIV, 999 = DCCCCXCIX и т. п.
         § 3. Древне-русская (византийская) система летосчисления. В древней Руси, как говорилось выше, была принята та же система летосчисления, которой придерживалась Византия. Именно, счёт лет велся от "сотворения мира". При этом исходили из предположения, что от "сотворения мира" до "рождества христова", или до эры, принятой большинством народов в настоящее время, прошло 5508 лет. Так продолжалось до конца XVII в., и только с 1700 г., по указу Петра I, Россия перешла на эру Дионисия, т. е. на летосчисление от "рождества христова". Вплоть до самой Октябрьской революции Россия пользовалась Юлианским календарём.
        Принимая во внимание указанное выше количество лет (5508 или 55 с лишним сотен), отделяющих эру от "сотворения мира" от эры Дионисия, мы можем вывести следующую таблицу основного соответствия между обоими системами летосчисления (конкордации дат). (См. таблицу I).

-24-

 Таблица I

Соответствие между системами летосчисления от "сотворения мира" и от "рождества христова".

Текущий век (столетие) по летосчислению от "рождества христова"

Количество законченных столетий, прошедших до текущего века по летосчислению от "рождества христова"

Соответствующее количество законченных столетий по византийскому летосчислению

 

В основном до текущего (от "р. хр.") века прошло столетий по счёту от "сотворения мира"

Последние годы текущеего (от "р. хр.") века падают на столетие по счёту от "сотворения мира"

 

X

9 столетий (900) 1)...

64 столетий (6400)

65 столетие (6500)

 

XI

10 " (1000) ...

65 " (6500)

66 " (6600)

 

XII

11 " (1100) ...

66 " (6600)

67 " (6700)

 

XIII

12 " (1200) ...

67 " (6700)

68 " (6800)

 

XIV

13 " (1300) ...

68 " (6800)

69 " (6900)

 

XV

14 " (1400) ...

69 " (6900)

70 " (7000)

 

XVI

15 " (1500) ...

70 " (7000)

71 " (7100)

 

XVII

16 " (1600) ...

71 " (7100)

72 " (7200)

 



        В таблице приведены обозначения столетий только для периода с Х по XVII вв. включительно, т. к. для времени, предшествующего X столетию, в древне-русских документах не встречаются точные датировки, а с XVIII в. уже входит в употребление система летосчисления от "рождества христова" и даты по Византийскому летосчислению больше не встречаются в источниках.
        Правила точного перевода дат с летосчисления от "сотворения мира" на современное будут даны ниже, в специальном разделе. Сейчас же необходимо познакомиться с некоторыми особенностями в обозначении дат в древне-русских документах, затрудняющими для неподготовленных лиц их понимание.
         § 4. Древне-русское обозначение дат. Надо иметь в виду, что в датах XV в. часто опускаются цифры тысячелетий и столетий и указываются только десятилетия и единицы годов. Например: "в лето (т. е .в году) 79". На месте недостающих в документе тысяч и сотен лет следует в этом случае подставить цифру 69. Следовательно, в полном виде дата будет выглядеть так: 6979.
        Точно так же в обозначениях дат XVII в. постоянно отсутствуют цифры тысячелетий и оставлены указания лишь на сотни, десятки и единицы лет, например: "лета (т. е. года) 142". В этом лучае надо дополнить пропущенную в документе цифру - 7 тысяч - и прочесть всю дату как: 7142.
        Подобные сокращения, как мы прекрасно знаем, не являются особенностью только древне-русской системы датировки. Ведь и в наше время часто говорят: "в 43-м году" (вместо: в 1943-м году), "Отечественная война 812-го" или просто "12-го года" (вместо: 1812-го года), "Революция 905-го" или "5-го года" (вместо: 1905 года) и т. д.
        ___________
        1) Многоточия указывают, что вслед за цифрами законченных столетий, должны итти соответственные обозначения десятков и единиц лет текущего века.

-25-

        Даты в древне-русских документах иногда указываются в цифрах (в виде буквенной цифири), иногда же приводится их словесное выражение. Так для 7074 года, например, мы можем встретить следующие обозначения: или

 

______  

"лета (т. е. года)1)    

‡ЗОД"

или "лета семь тысяч семьдесят четвёртого". В ряде случаев только часть даты дана при посредстве буквенной цифири, а другая часть названа словами. Например, для приведенного выше случая вполне возможны и такие варианты:

 

__

"лета   

‡З

  семьдесят четвертого";

или

 

____

"лета   

‡ЗО

  четвертого".

        При этом надо иметь в виду разницу между древне-русским словесным выражением чисел в пределах второго десятка и наименованием последующих десятков. Количественные и порядковые числительные от 11 до 19 включительно образуются из сочетания названий единиц, суффикса "на" и слова "десять". Например, "в лето первоенадесять" (в 11-м, т.е. 6911-м году); "лета семь (или седмь) тысяч четвёртогонадесять" (7014 года); "лета семь тысяч пятогонадесять" (7015 года) и т. д.
        Названия десятков от 20 до 90 включительно складываются из присоединения к названиям единиц слова "десять" (без суффикса "на"). Например: "лета девятьдесять первого" (91 года, т. е. 6991 года); "лета семь (или седмь) тысяч (или тысящ) четыредесять пятого" (7045 года); "лета семь тысяч двадесять пятого" (7025 года) и т. д.
        При указании столетий иногда приводятся имеющие значение сотен буквы-числа, в других же случаях документы пользуются буквами-числами, указывающими на соответствующие единицы, и сопровождают их словами: сот-сотен. Например: обозначение 6901 года может встретиться в документах в различных вариантах: или

 

____

"

‡SЦ

   первый".

или

 

____

"

‡S

  сот первый".

 

 

__

 

__

Вспомним, что 

Ц

 - 900, a  

- 9.

        Приводя даты в виде порядковых числительных, документы в некоторых случаях (согласно с современными правилами) придают грамматическую форму "который" только последним знакам многозначного числа. В других случаях порядковую форму получают словесные выражения всех (или почти всех) цифр даты. Например, для 6936-го года могут быть употреблены разные обозначения: "в лето шесть тысяч девятьсот тридесять шестое" или "в лето шесть тысячное и девятьсотное тридесять шестое". Точно также:

 

__

 __

 ____

"в лето 

‡S

 Ц

 ЛГ-е"

или же

 

__

 

 __

 

 ____

"в лето 

‡S

-ное

 Ц

-ное

 ЛГ-е".

        Наконец, следует упомянуть, что буквы-цифры, обозначавшие дату, писались как в слитной форме

 

______

 

("в лето 

‡SЦН

 - 6950"),

так и отделялись друг от друга союзом "и"

 

__

 

 __

 

 __

("в лето 

‡S

 и 

 Ц

 и 

 Н").

         § 5. Перевод дат (редукция) с древне-русской (византийской) эры на современную. Мартовский, и сентябрьский календарные стили.
        После того, как историк прочитает имеющуюся в документе
        ___________
        1) Слово "лето" употребляется в древне-русских источниках не только в значении "сезона", но преимущественно в смысле "год".

-26-

дату, он должен дать ее перевод на наше летосчисление. На первый взгляд эта задача больших трудностей не представляет. От "сотворения мира" до "рождества христова", как уже было указано, считалось 5508 лет. Поэтому для перевода даты с византийской эры на современную (эру Дионисия), очевидно, как правило, следует вычесть из этой даты цифру 5508. Например, мы встречаем в источнике указание на 7148 год от "Сотворения мира". 7148-5508 =1640. Следовательно, имеется в виду 1640 год от "рождества христова".
        Однако, это общее правило требует уточнения. Надо иметь в виду, что в древней Руси до конца XVII в. новый год начинался не с января, как в настоящее время, а с марта (как в древнем Риме) или с сентября (как в Византии). Только при Петре I, с 1700 г., одновременно с переходом на эру от "рождества христова" было решено началом года считать 1 января. До Петровской же реформы существовало два основных календарных стиля, отличных от современного: мартовский, согласно которому новогодие (подобно римскому обычаю) приходилось на 1 марта, и сентябрьский (заимствованный из Византии) с новогодием, падающим на 1 сентября. Самые термины "мартовский, сентябрьский год", "мартовский, сентябрьский стиль" не встречаются в источниках, а принадлежат позднейшим исследователям. До 1492 (7000) года, как полагают исследователи, оба стиля существовали параллельно. С 1492 г. завоёвывает преобладание сентябрьский стиль, вытесняющий мартовский.
        Надо иметь также в виду, что мартовский календарный стиль представлял в свою очередь несколько вариантов (ультра-мартовский, цирка-мартовский), о которых скажем ниже.
        Всё это нужно учитывать при переводе дат с византийской эры на современную.
        Предположим, нам дана дата какого-то исторического события - 6758 г. При этом нам известно, что это цифровое обозначение года приведено по календарному стилю, согласно которому год начинался с 1 марта и заканчивался 28 февраля. А соответствующий 6758 году, 1250 год нашей эры (6758 - 5508 = 1250) начинается, как мы знаем, с 1 января, т. е. на два месяца раньше и кончается 31 декабря. Отсюда совершенно очевидно, что первые два месяца (январь и февраль) 1250-го года приходятся не на 6758-й, а на более ранний, 6757 год от "сотворения мира". Январь же и февраль 6758 года, заканчивающие по старинному календарю этот год, придутся уже на 1251 год эры от "рождества христова".
        Таким образом, вытекает следующее правило перевода дат с византийской эры и мартовского календарного стиля на современное летосчисление и январский календарный стиль. Цифра 5508 вычитается только для тех исторических событий, которые произошли в один из месяцев с марта по декабрь включительно. Если же, событие случилось в январе или феврале, то вычитаемым при переводе служит число 5507.

-27-

        Возвратимся к нашему примеру с 6758 годом. Если эта дата сопровождается в источнике указанием, скажем, на 15 февраля, то руководствуясь только что сформулированным правилом, мы получим при переводе 15 февраля 1251 года (6758 - 5507). Если же в источнике будет иная ссылка, например, на 7 сентября, то применение указанного правила даст 7 сентября 1250 г. (6758-5508).
        Очень часто в источниках отсутствуют точные указания на месяц и число, и дело ограничивается глухой ссылкой на год. В таком случае мы лишены возможности дать точный перевод даты на наше летосчисление и вынуждены ограничиться датировкой в пределах двух возможных годов по эре от "рождества христова". А для этого следует прибегнуть в качестве вычитаемого к обоим цифрам: и к 5507, и к 5508.
        Теперь остановимся на тех датах, которые приводятся в источниках по сентябрьскому календарному стилю. Выше, в качестве примера, мы брали 7148 год от "сотворения мира". Он начинается с 1 сентября и заканчивается 31 августа. А соответствующий ему 1640 (7148-5508) январский год нашей эры наступит только 1 января, следовательно, на четыре месяца позднее. Поэтому первые четыре месяца 7148 года (сентябрь-декабрь) придутся не на 1640 год от "рождества христова", а на 1639-й. С другой стороны, сентябрь-декабрь месяцы 1640 года январского календарного стиля нашей эры падают на 7149 год сентябрьского календарного стиля византийского летосчисления.
        Выводим следующее правило: если событие, датированное по византийской эре и по сентябрьскому календарному стилю, произошло в период с января по август включительно, то для перевода даты этого события на нашу эру следует из цифрового обозначения года вычесть 5508. Для событий, падающих на период с сентября по декабрь включительно, вычитаемым является цифра 5509.
        Поэтому при сентябрьском календарном стиле: 18 июля 7148 г. = 18 июля 1640 г. (7148 - 5508); 5 ноября 7148 г. = 5 ноября 1639 г. (7148 - 5509).
        Если месяц сентябрьского стиля, на который падает событие не указан, вычитаем из даты, подлежащей переводу, оба числа - 5508 и 5509 и производим датировку по нашей эре в пределах двух ближайших лет (в данном случае 1639 и 1640 гг.).
        Общая формула перевода может быть также выведена при помощи таблицы, графически изображающей соотношение между календарными стилями: а) январским (современным) и мартовским и б) январским (современным) и сентябрьским. (См. таблицу II).
        Поскольку мартовский год начинается и оканчивается на два месяца после январского, совпадающими в обоих календарных стилях оказываются месяцы с марта по декабрь включительно. Обозначив подлежащую переводу на нашу эру дату мартовского стиля от "сотворения мира" через букву N, а искомый год январского стиля современного летосчисления через X, найдём, что X для периода с марта по декабрь включительно = N - 5508. Январь и февраль N-ного (мартовского года захватят уже следующий,

-28-

 Таблица II

Соответствие январского, мартовского и сентябрьского календарных стилей

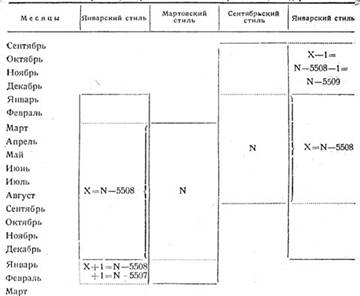
(Х + 1)-й январский год. Для того, чтобы определить, чему равен X + 1 (дата по современному летосчислению, соответствующая мартовскому стилю византийской эры для января и февраля), подставляем вместо X его значение: N - 5508. Получается следующее равенство: X + 1 = N - 5508 + 1 = N - 5507.
        Сентябрьский год начинается и кончается на четыре месяца раньше январского. Поэтому для дат сентябрьского стиля уравнение X = N- 5508 имеет силу в пределах периода с января до сентября. Месяцы с сентября по декабрь включительно N-ого сентябрьского года падают на предшествующий, (X-1)-й январский год. Заменив X равнозначным ему выражением: N - 5508, находим уравнение: X - 1 = N - 5508 - 1 - N - 5509. Эта формула и вступает в силу при переводе дат с византийской эры на современную для сентября-декабря сентябрьского стиля.
         § 6. Ультра-мартовский и цирка-мартовский календарные стили.
        Хорошее знакомство с мартовской и сентябрьской календарными системами представляет особенно большое значение для изучения древне-русской хронологии.
        В качестве разновидности мартовского года мы встречаемся ещё в источниках с датировкой на основе календарного стиля, называемого исследователями ультра-мартовским. Его сходство с

-29-

мартовским включается в том, что новогодие в обоих стилях приходится на 1 марта. Но ультра-мартовский календарный год, в противоположность мартовскому, не запаздывает на два месяца по сравнению с январским, а наоборот, начинается на десять месяцев ранее последнего.
        Графически взаимоотношение между мартовским, ультра-мартовским и январским календарными стилями можно выразить в виде таблицы III.

 Таблица III

Соответствие январского, мартовского и ультра-мартовского календарных стилей

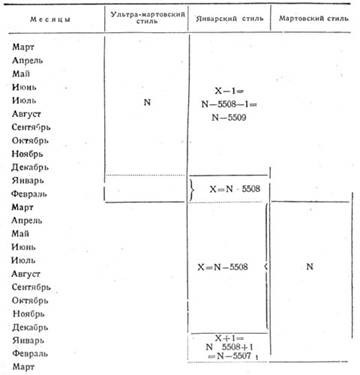
        Таким образом, мы видим, что совпадающими месяцами в N-ом ультра-мартовском году с январским (обозначаемым буквой X) являются январь и февраль, для которых перевод даты с византийскон эры на современную и производится по формуле: X = N - 5508. Месяцы ультра-мартовского N-oro года в преде-

-30-

лах с марта по декабрь включительно соответствуют (X-1)-му январскому году. Если X = N - 5508, то естественно, что-X-1 = N - 5508-1=N--5509. Следовательно, если подлежащая переводу на современное летосчисление дата византийской эры ультра-мартовского стиля падает на один из месяцев с марта по декабрь включительно, то вычитаемым служит цифра 5509.
        Сравнивая теперь между собою мартовскую и ультра-мартовскую системы, не трудно убедиться, что последняя ровно на год (двенадцать месяцев) предваряет первую. Отсюда - термин "ультра-мартовский",- от латинского слова "ультра" (ultra), что значит - по ту сторону: календарный год, предваряющий мартовский.
        Поэтому мы имеем полное право сказать, что перевод дат ультра-мартовского стиля с византийской эры на современное летосчисление подчиняется правилам, установленным для мартовского календаря, но с учётом этой разницы на один год. Другими словами, ультра-мартовский стиль византийской системы летосчисления предполагает, что от "сотворения мира" до "рождества христова" прошло не 5508, а 5509 лет. Поэтому в тех случаях, когда при переводе дат с мартовского стиля от "сотворения мира" на современное летосчисление мы вычитаем 5507 (для событий, случившихся в январе или феврале), при ультра-мартовской системе вычитаемым является число, большее на единицу, т. е 5508. Для событий, имевших место в период времени с марта по декабрь включительно, число 5508, подлежащее вычитанию при переводе дат с мартовского календаря византийской эры на эру от "рождества христова", точно так же увеличивается на единицу, и при ультра-мартовском счёте вычитается, следовательно, цифра 5509.
        Для того, чтобы наглядно представить себе, как при переводе дат с византийского летосчисления на современное, в зависимости от календарного стиля и от того месяца, на которое падает датируемое событие, изменяется цифра, подлежащая вычитанию, приведём таблицу IV.

 Таблица IV

Перевод дат с византийского летоисчисления на современное

Месяцы, на которые падает датируемое событие

Число, подлежащее вычитанию при

Мартовском стиле

Ультра-мартовском стиле

Сентябрьском стиле

Январь

-5507

-5508

-5508

Февраль

-5507

-5508

-5508

Март

-5508

-5509

-5508

Апрель

-5508

-5509

-5508

Май

-5508

-5509

-5508

Июнь

-5508

-5509

-5508

Июль

-5508

-5509

-5508

Август

-5508

-5509

-5508

Сентябрь

-5508

-5509

-5509

Октябрь

-5508

-5509

-5509

Ноябрь

-5508

-5509

-5509

Декабрь

-5508

-5509

-5509


-31-

        Наконец, в источниках мы можем (встретиться с дальнейшими разновидностями как мартовского, так и ультра-мартовского стилей. Их своеобразие заключается в том, что они не предполагают в качестве начала нового года постоянного числа, падающего обязательно на 1 марта. Новогодие не является твердо установленным. Оно из года в год колеблется около 1 марта, иногда предваряя это число, но большею частью следуя за ним. Как думают исследователи, указанные колебания объясняются тем, что новогодие стремились приурочить к первому весеннему полнолунию. А таковым считалось полнолуние, приходящееся или на конец февраля, или на март.
        Исследователи называют мартовский календарный год, подобного типа, (с переменным началом), цирка-мартовским или цирка-ультра-мартовским, в зависимости от того, следует ли он за январским, или предшествует ему. Латинское слово "цирка" (circa) --вокруг указывает на то, что новогодие колеблется в пределах ("вокруг") 1 марта.
        Само собою разумеется, что при переводе на современное летосчисление с византийской эры дат цирка-мартовского стиля остается в силе правило, что для событий, имевших место в январе и феврале, вычитается число 5507, а для периода с марта по декабрь -- 5508. Но эта общая формула требует одной поправки. Цифра 5508 вступает в силу в качестве вычитаемого для перевода дат событий, случившихся начиная не с 1 марта, а с того числа, которое в данном случае является начальным днем года.
        Например, если 6646 год начинается 27 марта, то при переводе этого года на нашу эру, для событий, падающих на период с 1 января по 26 марта включительно мы вычитаем из 6646 цифру 5507, а для событий, датируемых временем с 27 марта по 31 декабря включительно -- 5508.
        Аналогичное правило применяем и для цирка-ультрамартовского года, учитывая разницу между мартовским и ультра-мартовским стилями на 12 месяцев. Для событий, датируемых согласно цирка-ультра-мартовскому стилю, январем, февралем или мартом, но в пределах чисел до начала нового года, при переводе на современное летосчисление вычитается 5508, для остальных месяцев (после новогодия) по декабрь включительно -- 5509. Вернемся к вышеприведенному примеру с 6646 годом, предполагая, что дата дана по цирка-ультра-мартовскому стилю. Если событие произошло в течение января, февраля или первых 26 чисел марта, вычитаемым является число 5508. Для последних дней марта (с 27-го числа), и следующих месяцев (апреля -- декабря), вычитаемое -- 5509.
        Детальное знакомство со всеми рассмотренными выше календарными стилями имеет значение при изучении источников до конца XV в., когда окончательно вступает в силу сентябрьский счет, при чем преимущественно при изучении источников литературного характера, главным образом летописных сводов. Что же касается древне-русских акстов, то в них с самого начала преобладает датировка сентябрьскими годами. Надо также иметь в виду, что многие древнейшие акты XIV-XV вв. вообще лишены дат.

-32-

        В дальнейшем мы сосредоточим наше внимание особенно на мартовском и сентябрьском стилях, так как из вышеизложенного очевидно, что ультра-цирка-мартовские системы представляют собою лишь простые варианты мартовского счета. Их мы оставим в стороне.
        Основной вопрос, возникающий перед исследователем, прежде чем он приступит к переводу с византийской эры на современное летосчисление имеющейся в источнике даты, сводится к установлению того стиля, каким пользуется источник. Как разрешить этот вопрос? Надо сразу сказать, что это задача далеко не такая простая. И нельзя рекомендовать какой-либо один рецепт, пригодный для всех случаев. Приходится прибегать к ряду приемов в зависимости от того, какие дополнительные указания сопровождают в источнике ссылку на год, месяц, число. Методы выявления календарных стилей, принятых в различных источниках при датировке исторических событий, будут рассмотрены в дальнейших разделах.
        Надо также иметь в виду, что перевод дат с византийской эры на современную происходит по Юлианскому календарю, т. е. по "старому стилю". Для того, чтобы выразить дату конца XVI --XVII вв. по Григорианскому календарю ("новому стилю"), мы должны ее увеличить на 10 дней. Даты до конца XVI в. (до 1582 г.) естественно нельзя перевести на "новый" стиль: в то время он еще не был введен.
         § 7. Индикты. Счет индиктами, или пятнадцатилетними периодами, заимствован в дровней Руси из Византии. Индиктом называется порядковое место данного года в пределах текущего пятнадцатилетнего цикла, при чем исходной точкой этого циклического счета являетей византийская эра -- "сотворение мира", а смена индиктов в каждом цикле совершается в день византийского новогодия -- 1 сентября.
        Этимология слова "индикт", так же, как и происхождение самой системы, выяснены недостаточно. Повидимому, счет индиктами ведет свое начало от тех переписей населения, которые раз в 15 лет производились в Римской империи и в Византии. В Византии индикты введены в 313 г. н. э.
        Каким образом найти индикт какого-либо интересующего нас года? Предположим, нам дан 6973 год по византийской эре. Прежде всего мы узнаем, сколько прошло от "сотворения мира" до указанной даты законченных пятнадцатилетних циклов. Для этого делим число 6973 на 15. Полученное частное (464) дает ответ на этот предварительный вопрос. Но основной интерес для нас представляет не частное, а остаток (13). Он указывает, что 6973 год занимает 13-е место в незавершившемся 465-м пятнадцатилетнем периоде от "сотворения мира". Это цифровое указание на порядковое место, или, как говорят, порядковый номер данного года, и является его индиктом. Таким образом, индикт 6973 г. = 13.
        Отсюда общее правило определения индикта любой даты сводится к нахождению остатка от деления цифрового обозначения данного года от "сотворения мира" на 15. Бели в результате деле-

-33-

ния остатка не получается, то индикт приравнивается делителю, т. е. цифре 15.
        Далее следует иметь в виду, как было уже указано выше, что индиктный счет ведется от 1 сентября до 1 сентября следующего года. Поэтому, одна и та же дата, приведенная по двум календарным стилям (мартовскому и сентябрьскому), будет иметь общий индикт только для месяцев, совпадающих в обоих календарях, именно, с марта по август включительно. Для периода с января по февраль и с сентября по декабрь включительно индикт мартовского года будет на единицу больше сентябрьского, т. к. мартовский календарный счет, как мы видели .выше, расходится с сентябрьским.
        При определении индиктов для дат от "рождества христова" предварительно следует произвести перевод этих дат на летосчисление от "сотворения мира", а затем уже приступить к вычислению остатка от деления их на 15.
        В целях облегчения работы по отысканию индиктов для дат различных стилей существует специальная таблица, которая приводится ниже. (См. таблицу V).
        Пользоваться этой таблицей очень не сложно. В верхней ее части помещены справа тысячелетия и столетия эры от "рождества христова", слева -- тысячелетия и столетия от "сотворения мира". Внизу, в средней части, находятся цифры десятков и единиц годов для дат обоих летосчислений, справа и слева -- числа индиктов. Индикт для даты по современному летосчислению расположен на пересечении вертикали, проведенной сверху вниз от нужной цифры тысячелетий и столетий, и горизонтали, идущей слева направо от соответственной цифры десятков и единиц. Горизонтальная линия, направленная от данного числа десятков влево, на месте своего пересечения с вертикальной линией, опущенной сверху от тысячелетий и столетий, покажет индикт для даты византийской эры.
        Надо иметь при этом в виду, что табличный индикт, найденный для дат современной эры, следует увеличить на единицу в том случае, если событие произошло в один из месяцев с сентября то декабрь включительно. Для периода с января по август включительно табличный индикт остается в силе, т. к. эти месяцы январского года совпадают с соответственными месяцами сентябрьского календарного стиля, по которому ведется счет индиктов. Аналогичное правило следует учитывать для мартовского календарного стиля византийской эры. В пределах совпадающего с сентябрьским календарем периода мартовского года (с марта по август включительно) мартовский индикт равен сентябрьскому, т. е. табличному. Для остальных месяцев (январь -- февраль, сентябрь -- декабрь), к индикту, найденному по таблице, следует прибавить лишнюю единицу.
        Какое практическое значение дли историка имеет знание правил нахождения индиктов дли любых дат различных систем летосчисления я календарных стилей? Чтобы в должной мере оценить всю важность знакомства с индиктным счетом при работе над изучением

-34-

 Таблица V

Индикты

7300

7400

7500

От
"сотво-
рения
мира"

Тысячи и сотни годов

От
"рож-
дества
христова"

1800

1900

2000

7000

7100

7200

1500

1600

1700

6700

6800

6900

1200

1300

1400

6400

6500

6600

900

1000

1100

6100

6200

6300

600

700

800

5800

5900

6000

300

400

500

5500

5600

5700

Десятки и единицы годов

0

100

200

10

5

15

0

15

30

45

60

75

90

3

13

8

11

6

1

1

16

31

46

61

76

91

4

14

9

12

7

2

2

17

32

47

62

77

92

5

15

10

13

8

3

3

18

33

48

63

78

93

6

1

11

14

9

4

4

19

34

49

64

79

94

7

2

12

15

10

5

5

20

35

50

65

80

95

8

3

13

1

11

6

6

21

36

51

66

81

96

9

4

14

2

12

7

7

22

37

52

67

82

97

10

5

15

3

13

8

8

23

38

53

68

83

98

11

6

1

4

14

9

9

24

39

54

69

84

99

12

7

2

5

15

10

10

25

40

55

70

85

 

13

8

3

6

1

11

11

26

41

56

71

86

 

14

9

4

7

2

12

12

27

42

57

72

87

 

15

10

5

8

3

13

13

28

43

58

73

88

 

1

11

6

9

4

14

14

29

44

59

74

89

 

2

12

7

Индикты

Десятки и единицы годов

Индикты


первоисточников, необходимо ясно себе представить, в каких формах может встретиться исследователю в исторических памятниках ссылка на индикты?
        Возможны два варианта: 1) индикт заменяет собою обозначение года, который вовсе не указан в источнике; 2) индикт дополняет указание на год и полная дата приводится в следующих выражениях: "лета такого-то, индикта такого-то".
        Казалось бы, в обоих случаях обращаться к помощи индикта для датировки памятника совершенио бесполезно и историк вправе его игнорировать. В самом деле, если мы знаем про какое-то событие, что оно совпало, например, с 12-м индиктом, но нам не

-35-

известен из источника год, к которому это событие относится, то мы как будто бы бессильны отыскать действительную дату. Ведь лет, соответствующих 12-му индикту, такое большое количество: один раз в каждое пятнадцатилетие нам обязательно встретится год с порядковым номером 12.
        С другой стороны, если источник сам сообщает год, то какой смысл имеет при этом историку учитывать дополнительную ссылку на индикт? Не безразлично ли в конце концов, какое порядковое место занимает интересующий нас год в пределах того или иного текущего пятнадцатилетнего периода от "сотворения мира"? Для нас как будто важно цифровое обозначение года само по себе, и только.
        Однако в действительности индикт выполняет при датировке источников значительно более серьезную роль, чем это может показаться с первого взгляда. Мы легко в этом убедимся, внимательно присмотревшись к двум приведенным выше возможным случаям датировки, с привлечением в той или иной форме индикта.
        Если в документе отсутствует год, к которому относится его возникновение, но помечен индикт, то сам по себе последний, конечно, не достаточен для точной датировки. Но при наличии некоторых косвенных признаков индикт помогает исследователю уточнить дату даже при отсутствии в источнике непосредственного цифрового обозначения интересующего нас года. Например, если мы встретим в источнике 14-й индикт и если нам известно, что этот источник относится, скажем, ко времени великого московского князя Ивана III (пусть это будет хотя бы жалованная грамота, выданная Иваном III), то зная начальную и конечную даты княжения последнего (6970--7013 или 1462--1505), мы легко установим по таблице, что 14-й индикт соответствует или 1466, или 1481, или 1496 гг.1) Конечно, вряд, ли исследователь в поисках даты источника удовлетворится подобным итогом, далеким от абсолютной точности. Но все же индикт помог нам в пределах сорока с лишним возможных лет остановить свой выбор только на трех и исключить все остальные, как явно непригодные для датировки: А привлечение каких-либо дополнительных косвенных признаков, быть может, укажет, какая же из этих трех дат является наиболее вероятной или даже единственно возможной.
        Разберем другой вариант. В источнике приведены одновременно и год и индикт. В этом случае последний помогает установить тот сталь (мартовский или сентябрьский), по которому приведена дата. А это важно, чтобы знать какое число следует вычесть для
        ___________
        1) В данном случае пользоваться таблицей надо следующим образом. Ищем в правой верхней части таблицы, в двух графах те два столетия "от рождества христова", которые захватывает княжение Ивана III (1400 и 1500). Спускаемся от найденных цифр по соответственным вертикалям вниз, останавливаясь в обоих случаях на цифровом обозначении 14 индикта, имеющемся в каждой графе. Затем от цифры 14 по двум же графам поворачиваем влево к числам десятков и единиц годов, соответствующих найденным выше столетиям. Все эти годы падают на 14-й индикт, но мы выбираем из них лишь те, которые укладываются в пределы княжения Ивана III (между 1462 и 1505 годами).

-36-

перевода даты на нашу эру. Например, если нам, указано, что событие произошло в 6905 г. в феврале месяце индикта 5-го, то для нас очевидно, что мы имеем дело с.сентябрьским стилем, т. к. по таблице можно установить, что 6905-му году соответствует 5-й индикт. Если для февраля 6905 г. в источнике указан 6-ой индикт, то это свидетельствует о датировке по мартовскому стилю, т. к. в таблице находим для 6905 г. цифру индикта 5, которую в случае датировки мартовским стилем (в пределах января -- февраля и сентября -- декабря) следует увеличить на единицу. Если мы придем, на основании индикта, к выводу, что перед нами сентябрьский стиль, то поскольку событие относится к февралю, мы при переводе даты на наше летосчисление, должны будем вычесть цифру 5508. В случае мартовского стиля вычитаемым явится 5507.
        Пользуясь индиктным счетом, заимствованным из Византии, древне-русские писцы не всегда учитывали колебаний индиктов, происходивших от разницы мартовского (русского) и сентябрьского (византийского) стилей, и поэтому, проставляя индикты, допускали иногда ряд ошибок. Это обстоятельство также необходимо принимать во внимание при изучении хронологических данных древне-русских источников и в первую очередь, летописных сводов.
         § 8. Календы. Кроме датировки индиктами, в древне-русских источниках (летописных сводах) иногда (правда, очень редко) встречаются указания на римские календы. Это главным образом относится к памятникам письменности новгородского происхождения, поскольку Новгород был более тесно связан с Западной Европой. Так в Новгородской летописи под 6644 (1136) г. имеются следующие хронологические данные: "месяца июля 19 преже 14 каланда августа". Мы уже знаем, что календами в Риме назывались первые числа месяцев, при чем календный счет велся не вперед, а назад. Приведенный летописный текст следует понимать в том смысле, что 19 июля является 14-м днем до августовских календ, т. е. до 1 августа.
         § 9. Месяцы и сезоны. В древней Руси, как мы знаем, был принят Юлианский календарь. Поэтому год, как и в настоящее время, делился на 12 месяцев. Их названия воспроизводят наименования месяцев древне-римского календаря, заимствованные из латинского языка. Однако, в некоторых древнейших памятниках письменности (например, в Остромировом евангелии XI в.) сохранились более ранние, чисто славянские, названия месяцев, происхождение которых имеет определенную связь с наблюдениями над сменой явлений природы. С некоторыми изменениями эта древнеславянская номенклатура дожила и до настоящего времени в ряде славянских языков. Так январю соответствовало название просинец (т. к. в это время становилось светлее), февралю -- сечень (т. к. это был сезон вырубки леса), марту -- сухий (т. к. в некоторых местах уже подсыхала земля), апрелю -- березень, березозол (имена, связанные с березой, начинающей цвести), маю -- травень (от слова "трава"), июню -- изок (кузнечик), июлю -- червень, серпень (от

-37-

слова "серп", указывающего на время жатвы), августу -- зарев (от "зарево"), сентябрю -- рюен, октябрю -- листопад, ноябрю -- декабрю -- грудень (от слова "груда" -- мерзлая колея на дороге), иногда -- студень.
        Трудно оказать, в какой мере этот древнейший славянский календарь отличался от принятого в настоящее время, как по количеству месяцев (некоторые славянские названия, например грудень, соответствуют двум нашим месяцам), так и по их продолжительности. Во всяком случае почти во всех, даже самых ранних источниках, господствует уже современный календарь. В его основу, как указано, положен календарь древне-римский, в сложившемся виде состоявший из двенадцати месяцев. Это -- януариус (от имени Януса -- бога открытых дверей; месяц -- открывающий год); фебруариус (от слова februm -- очищение; месяц покаяния, очищения, поклонения мертвым); мартиус (от имени бога войны -- Марса); априлис (от слова "aperire" -- раскрывать; месяц (раскрывающихся на деревьях почек); маиус (от имени богини Майи); июниус (от имени богини Юноны); июлиус (в честь Юлия Цезаря) аугустус (в честь императора Августа); септембер (седьмой то порядку, считая началом года не январь, а март); октобер (восьмой); новембер (девятый); децембер (десятый). Вначале римляне (считали десять месяцев, первым из которых был март, последним -- децембер. Позднее к началу года были присоединены януариус и фебруариус.
        Все эти латинские имена приобрели русифицированную форму: январь, февраль, март, апрель, май, июнь, июль, август, сентябрь, октябрь, ноябрь, декабрь. Но в некоторых, наиболее ранних источниках они встречаются и в форме, совсем приближающейся к латинскому прообразу: енуар (генуар, генварь), фебруар (февруар), априль, иуний, иулий, аугуст, сепптеврий (сентямбрь, септябрь), октомбрий (охтоврий), новембрий, декембрий.
        Указание на месяцы, сопровождающее даты византийского летосчислении, часто дает :ключ к определению того календарного стиля, по которому эти даты приведены. Предположим, что в каком-либо летописном своде мы находим следующий ряд погодных известий:
        6843 г. июня ... (случилось такое-то событие)
        6843 г. августа ... (" " " )
        6843 г. декабря ... (" " " )
        Совершенно очевидно, что перед нами не сентябрьский стиль, согласно которому начало года падает на 1 сентября, и поэтому за датой "6843 г. августа" никак не могла бы следовать дата --"6843 г. декабря", а естественно было бы ожидать: "6844 г. декабря". Следовательно, летописец пользуется мартовской системой, или одной из ее разновидйостей (ультра-мартовской, цирка-мартовской)..
        Иногда в источниках, вместо месяцев, имеются указания на сезоны: зиму, лето, весну, осень. Но точных границ между сезонами установлено, повидимому не было.
         § 10. Недели. Счет, дней неделями, возникший на Востоке и принятый в настоящее время большинством народов, существовал

-38-

в России с древнейших пор; как и теперь, неделя складывалась из семи суток. Отсюда -- встречающееся в источниках название недели "седмицей".
        Названия дней недели у большинства европейских народов заимствованы от наименования тех планет, которым отдельные дни были посвящены. А планеты, в свою очередь, получили, свои названия от имен римских богов. Так в ряде романских языков понедельник именуется днем луны, вторник -- Марса, среда -- Меркурия, четверг -- Юпитера, пятница -- Венеры, суббота -- Сатурна. Воскресенье -- это день солнца.
        Происхождение русских названий совсем иное. Вместо "воскресенья" в древне-русских документах употреблялось обычно слово "день недельный" и наряду с ним просто "неделя", т. е. день отдыха, свободный от всякого дела. С воскресного дня термин "неделя", был перенесен затем на весь семидневный период. Понедельник, как показывает самое название, это -- день, идущий непосредственно после воскресенья или недели. Вторник -- второй по счету день вслед за воскресеньем. Среда (середа) -- середина недели (в смысле семидневного периода). Четверг и пятница ("часто встречающиеся в источниках в форме "четверток" и "пяток") -- это дни, занимающее четвертое и пятое порядковые места, считая от воскресенья. Некоторым своеобразием отличается название "суббота", которое происходит от еврейского слова "сабат" (шабаш), т. е. конец (семидневки), покой.
        Трудно с достоверностью сказать, с какого дня начинался в древней Руси счет дней недели: с воскресенья ли, заканчиваясь субботой, или же с понедельника по воскресенье. Предполагают, что единой системы и не было, что существовали параллельно оба указанных счета, причем, в житейском обиходе был в ходу первый, в церковной практике преобладал второй.
         § 11. Круги солнца. Календарный год не содержиг в себе полного количества недель. В простом году заключается 52 недели и один лишний день (52 х 7 + 1 = 365), в високосном -- 52 недели и два дня (52 х 7 + 2 = 366). Поэтому одни и те же числа месяцев не могут из года и год падать на одни и те же дни недели. Каждый простой год заканчивается тем самым днем недели, с которого он начался. Но новый календарный год, наступающий после простого, будет естественно начинаться со дня недели, непосредственно следующего за тем, которым открывался и завершался предшествующий год. Соответственным образом, конечно, в новом году перемещаются в пределах недели на один день по сравнению с предшествующим годом и все прочие числа с начала и до конца. Предположим, что 1 января N-ого (простого года падало на воскресенье, 2-е -- на понедельник, 3-е -- на вторник и т. д., вплоть до 31 декабря, которое, как и 1 января, обязательно совпадает с воскресеньем. В (N + 1)-м году t января придется уже в понедельник, 2-е -- во вторник, 3-е -- в среду... 31 декабря, как и 1-е января, -- в понедельник.
        В новом году, наступающем после високосного, все числа перемещаются по сравнению с предшествующим в пределах недели.

-39-

само собой разумеется, не на один, а на два дня. Поэтому если N-ый год, начинающийся с воскресенья, окажется високосным, то 1 января следующего (N + 1)-го года будет не в понедельник, как в ранее рассмотренном примере, а во вторник.
        Таким образом, если мы возьмем за исходный пункт наших наблюдений начало любого N-ного года, т. е. 1 января, и проследим, как это число (а в связи с ним и все прочие числа) переходят по дням недели в каком-то цикле непосредственно следующих за N-ным годом календарных лет, то заметим в этом перемещении определенный порядок, причем легко убедиться, что этот порядок буквально повторяется через каждые 28 лет.
        Приводимая ниже таблица VI наглядно демонстрирует правильность указанного наблюдения.

 Таблица VI

Двадцативосьмилетний солнечный цикл

Порядковые
NN годов

Дни недели, на
которые падает
новогодие

Порядковые
NN годов

Дни недели, на
которые падает
новогодие

Порядковые
NN годов

Дни недели, на
которые падает
новогодие

Порядковые
NN годов

Дни недели, на
которые падает
новогодие

1

Воскресенье

15

Среда

29

Воскресенье

43

Среда

2

Понедельник

16

Четверг

30

Понедельник

44

Четверг

3

Вторник

17

Суббота

31

Вторник

45

Суббота

4

Среда

18

Воскресенье

32

Среда

46

Воскресенье

5

Пятница

19

Понедельник

33

Пятница

47

Понедельник

6

Суббота

20

Вторник

34

Суббота

48

Вторник

7

Воскресенье

21

Четверг

35

Воскресенье

49

Четверг

8

Понедельник

22

Пятница

36

Понедельник

50

Пятница

9

Среда

23

Суббота

37

Среда

51

Суббота

10

Четверг

24

Воскресенье

38

Четверг

52

Воскресенье

11

Пятница

25

Вторник

39

Пятница

53

Вторник

12

Суббота

26

Среда

40

Суббота

54

Среда

13

Понедельник

27

Четверг

41

Понедельник

55

Четверг

14

Вторник

28

Пятница

42

Вторник

56

Пятница

        Сравнение между собой 1--2-ой граф таблицы с графами 3--4-ой отчетливо показывает, что в пределах двух произвольно взятых 28-летних циклов имеется полное соответствие в порядке следования одних и тех же чисел месяцев по дням недели. Продолжив нашу таблицу далее, мы так же легко бы установили, что это соответствие возобновляется периодически через каждые 28 лет Построенный на указанном наблюдении 28-летний период носит название цикла солнца. Счет циклами солнца был очень распространен в древней Руси, причем исходной точкой для этого счета служило "сотворение мира".
        Порядковое место, занимаемое тем или иным годом в пределах какого-то незаконченного цикла солнца, -- называется кругом солнца данного года.

-40-

Приемы вычисления круга солнца аналогичны методам определения индикта. Цифровое обозначение интересующего нас года от "сотворения мира" делится на 28, причем частное устанавливает количество полных циклов солнца, прошедших до данного года, а остаток указывает на круг солнца последнего, т. е. на его порядковый номер в текущем 28-летнем цикле. Например, круг солнца 6758 г. = 10 (6758 : 28 = 241 полных циклов солнца + 10 в остатке).
        Если при вычислении круга солнца мы имеем дело с датой от "рождества христова", то в этом случае нужно учесть, что к началу нашей эры закончился 20-й год текущего цикла солнца. В самом деле, современное летосчисление началось в 5508-м году от "сотворения мира". Круг же солнца: 5508 года равен 20 (5508 : 28=196 полных циклов солнца + 20 в остатке). Поэтому к интересующему нас году от "рождества христова", в целях установления его круга солнца, предварительно надо прибавить цифру 20 и уже над полученной суммой производить соответственные арифметические действия, указанные выше для дат византийской эры: деление на 28 и выявление остатка. Круг солнца 1943 г. равен 3, т. к. (1943 + 20) : 28 дает в остатке 3.
        Круг солнца можно найти и без всяких вычислений, по таблице VII, помещаемой ниже. Пересечение двух линий, проведенных сверху вниз от цифры тысячелетий и столетий данной даты (приведенной как по византийской, так и то современной эре) и слева направо от цифры десятков и единиц годов, укажет круг солнца интересующего нас года.
         § 12. Вруцелета. Дни недели в пределах года обозначаются в древне-русских календарях семью буквами алфавита, соответствующими первым семи цифрам (А, В, Г, Д, Е, S, 3), расположенным по следующему принципу:
        Началом тода считается 1 марта. Предполагается, что в 1-м году византийской эры ("от сотворения мира"), совпавшим с началом первого круга солнца, 1 марта приходилось в пятницу. Следовательно, ближайшее воскресенье после новогодия -- 3 марта. Этот день и был обозначен первой буквой алфавита -- А. Следующие дни недели получили для своего обозначения остальные шесть начальных букв, причем в порядке, обратном алфавиту. В результате перед нами такая картина:
        1 марта (пятница) -- Г
        2 марта (суббота) -- В
        3 марта (воскресенье) -- А
        4 марта (понедельник) -- 3
        5 марта (вторник) -- S
        6 марта (среда) -- Е
        7 марта (четверг) -- Д
        8 марта (пятница) -- Г
        9 марта (суббота) -- S
        10 марта (воскресенье) -- А
        11 марта (понедельник) -- 3
        12 марта (вторник) -- S

-41-

 Таблица VII

Круги солнца

Десятки и единицы 
годов

\

Тысячи и сотни
годов

7300
6600
5900

7400
6700
6000

7500
6800
6100

6900
6200
5500

7000
6300
5600

7100
6400
5700

7200
6500
5800

1400
700
0

1500
800
100

1600
900
200

1700
1000
300

1800
1100
400

1900
1200
500

2000
1300
600

0
1
2
3

28
29
30
31

56
57
58
59

84
85
86
87

20
21
22
23

8
9
10
11

24
25
26
27

12
13
14
15

28
1
2
3

16
17
18
19

4
5
6
7

4
5
6
7

32
33
34
35

60
61
62
63

88
89
90
91

24
25
26
27

12
13
14
15

28
1
2
3

16
17
18
19

4
5
6
7

20
21
22
23

8
9
10
11

8
9
10
11

36
37
38
39

64
65
66
67

92
93
94
95

28
1
2
3

16
17
18
19

4
5
6
7

20
21
22
23

8
9
10
11

24
25
26
27

12
13
14
15

12
13
14
15

40
41
42
43

68
69
70
71

96
97
98
99

4
5
6
7

20
21
22
23

8
9
10
11

24
25
26
27

12
13
14
15

28
1
2
3

16
17
18
19

16
17
18
19

44
45
46
47

72
73
74
75

 

8
9
10
11

24
25
26
27

12
13
14
15

28
1
2
3

16
17
18
19

4
5
6
7

20
21
22
23

20
21
22
23

48
49
50
51

76
77
78
79

 

12
13
14
15

28
1
2
3

16
17
18
19

4
5
6
7

20
21
22
23

8
9
10
11

24
25
26
27

24
25
26
27

52
53
54
55

80
81
82
83

 

16
17
18
19

4
5
6
7

20
21
22
23

8
9
10
11

24
25
26
27

12
13
14
15

28
1
2
3

        Словом, каждому дню недели в пределах года соответствует своя постоянная буква. Буква, указывающая на воскресные дни, носит название: "вруцелето". В данном случае вруцелетом года является буква А.

-42-

        Останется ли вруцелето неизменным и в будущем году? Данный год начался пятницей, а следовательно, как мы знаем, пятницей и закончится. Новогодие (1марта) следующего года будет в субботу, 2 марта придется на воскресенье. Против 2 марта, как указано, стоит буква В, на которую упадут и все остальные воскресные дни года. Итак, вруцелето этого года -- В.
        Следующий (третий) год качнется с воскресенья и т. к. 1 марта (воскресный день), как мы видели, обозначено буквой Г, то эта буква я явится вруцелетом третьего года.
        Продолжая наши дальнейшие наблюдения над сменой вруцелета из года в год, мы убеждаемся, что эта смена происходит в порядке букв алфавита, причем после високосного года естественно произойдет скачок через букву. Например, если N-ый год с вруцелетом Г принадлежит к числу високосных, то вруцелетом (N + 1)-го года окажется не Д, а Е.
        Таким образом, смысл обозначения дней недели в пределах года семью начальными буквами в обратной алфавиту последовательности сводится именно к тому, что этим достигается перемещение вруцелета из года в год в алфавитной системе с интервалом в одну букву через каждые четыре года.
        Выше, говоря о цикле солнца, мы установили, что порядок передвижения одних и тех же чисел месяцев по дням недели периодически повторяется через каждые 28 лет. Это общее правило приложимо, конечно, в частности и к вруцелетам, т. е. к буквенным обозначениям специально воскресных дней различных лет. Наблюдается полное соответствие порядка смены вруцелет по годам в пределах следующих друг за другом 28-летних солнечных циклов. А отсюда вытекает и дальнейший вывод: каждому кругу солнца т. е. порядковому номеру того или иного года в пределах любого 28-летнего цикла, соответствует какое-то определенное вруцелето.
        Взаимоотношение между кругами солнца и вруцелетами дает таблица VIII.

 Таблица VIII

Соответствие между кругами солнца и вруцелетами

Круги солнца

Вруцелета

1

7

12

18

А

2

13

19

24

В

3

8

14

25

Г

9

15

20

26

Д

4

10

21

27

Е

5

11

16

22

S

6

17

23

28

З

        Таким образом, по кругу солнца любого года можио, пользуясь указанной таблицей, найти вруцелето последнего. Что же касается круга солнца, то для его определения достаточно или простых арифметических действий или же таблицы VII, приведенной выше.

-43-

        Но вруцелето данного года мож:но установить и не вычисляя предварительно круга солнца. Для этого (следует воспользоваться таблицей IX, специально для этой цели составленной.
        Вруцелето данного года находится на пересечении двух линий: вертикальной, проведенной сверху вниз от цифры, соответствующей тысячелетиям и столетиям даты 1), и горизонтальной, проведенной слева направо от числа ее десятков и единиц.
         § 13. Определение дня недели. Установление вруцелет для различных исторических дат имеет значение потому, что по вруцелетам мы всегда можем узнать, на какой день недели в том или ином году приходится любое, число любого месяца.
        Очень часто в источнике детально обозначается не только год, месяц и число, когда произошло интересующее нас событие, но имеется ссылка также и на день недели. И вот эта дополнительная ссылка в ряде случаев помогает проверить дату. Если, мы сумеем установить, что в данном году приведенный в источнике день недели не мог совпасть с указанным в нем числом месяца, то мы тем самым поставим под сомнение правильность всей даты. Если в дате имеется несоответствие между годом и индиктом, проверка, (произведенная при помощи оказавшегося в источнике названия дня недели, дает возможность также уточнить год, на который падает событие. Наконец, благодаря указанию на день недели, мы оказываемся а состоянии установить календарный стиль (мартовский или сентябрьский) года от "сотворения мира". Ведь по мартовскому счету числа ряда месяцев даты византийской эры (придутся не на те дни недели, на которые упадут соответственные числа сентябрьского стиля. А выяснение календарной системы важно, как мы знаем, для перевода дат византийского летосчисления на нашу эру.
        Ниже помещаем специальную таблицу X, служащую для определения того дня недели, на который приходится в указанном году любое число любого месяца. Для пользования таблицей необходимо предварительно найти тем или иным указанным выше способом вруцелето интересующего нас года.
        В таблице одни и те же месяцы года помещены в трех основных графах, соответствующих календарным стилям: январскому, мартовскому и сентябрьскому.
        Если дата дана от "рождества христова", то очевидно, имеется в виду январский счет. Ищем в соответственной графе указанный нам в дате месяц (учитывая также подразделения графы для простых и високосных лет), поднимаемся по вертикали вверх и находим указанное нам число месяца. Проведя от этого числа горизонтальную линию вправо, останавливаемся на том дне недели, который помещен в графе, соответствующей вруцелету данного года (найденному предварительно).
        Если год приведен по византийской эре, то мы поочередно обращаемся к графам мартовского и сентябрьского календарных
        ___________
        1) В зависимости от того, по какому летосчислению приведена дата (византийскому или современному), мы ищем тысячелетия и столетия в соответствующей графе.

-44-

 Таблица IX

Вруцелета

Десятки и единицы
годов

\

Тысячи и сотни 
годов

от сотв.
мира

6900
6200
5500

7000
6300
5600

7100
6400
5700

7200
6500
5800

7300
6600
5900

7400
6700
6000

7500
6800
6100

от рожд. 
христ.

1700
1000
300

1800
1100
400

1900
1200
500

2000
1300
600

1400
700
0

1500
800
100

1600
900
200

Вруцелета годов

0. 6. -. 17. 23. 28. 34. -. 45. 51. 56. 62. -. 73. 79. 84. 90. -

А

З

S

Е

Д

Г

В

1. 7. 12. 18. -. 29. 35. 40. 46. -. 57. 63. 68. 74. -. 85. 91. 96

В

А

З

S

Е

Д

Г

2. -. 13. 19. 24. 30. -. 41. 47. 52. 58. -. 69. 75. 80. 86. -. 97

Г

В

А

З

S

Е

Д

3. 8. 14. -.25. 31. 36. 42. -. 53. 59. 64. 70. -. 81. 87. 92. 98

Д

Г

В

А

З

S

Е

-. 9. 15. 20. 26. -. 37. 43. 48. 54. -. 65. 71. 76. 82. -. 93. 99

Е

Д

Г

В

А

З

S

4. 10. -. 21. 27. 32. 38. -. 49. 55. 60. 66. -. 77. 83. 88. 94. -

S

Е

Д

Г

В

А

З

5. 11. 16. 22. -. 33. 39. 44. 50. -. 61. 67. 72. 78. -. 89. 95. -

З

S

E

Д

Г

В

А

-45-

стилей и применяя аналогичные приемы, устанавливаем, по какому из них названное в источнике число месяца приходится на указанный там же день недели.
        Кроме таблиц, для определения дня недели существуют также специальные формулы. Они применимы в отношении дат от "рождества христова", причем Юлианского, а не Григорианского календаря. Нам нет надобности подробно останавливаться на выводе этих формул, требующих специальных сложных математических вычислении. Историк вправе использовать для своих целей результаты этих вычислений. Вот одна из этих формул, предложенная Д. Перевощиковым:
        Х = остатку от деления выражения [(N - 1) + 14(N - 1) + (Т - 1)] : 7
        Через X обозначается порядковый номер искомого дня недели, считая первым днем воскресенье, вторым -- понедельник, третьим -- вторник, четвертым -- среду, пятым -- четверг, шестым --пятницу, седьмым -- субботу. Под N подразумевается цифровое обозначение интересующего нас года от "рождества христова", Выражение (N- 1) определяет количество полных лет, закончившихся ранее N-oro года. Выражение 14 (N - 1) указывает на то число високосных лет, которое заключает в себе период от начала современной эры до иаступления N-ого года. Т -- количество дней, прошедших с начала N-ого года до указанного в источнике числа месяца включительно. Вычитая из Т одну единицу, мы тем самым из числа дней, прошедших от начала того года, для которого определяется день недели, до искомой даты, исключаем последнее, наступившее число месяца.
        Последовательность действий, предусмотренных формулой Перевощикова, выяснится из следующего примера.
        Предположим, что мы хотим знать, на какой день недели падало в 1643 г. 3 апреля. Берем цифру полных лет, прошедших до данного года, или другими словами, цифровое обозначение предшествующего года -- 1642. Узнаем далее количество високосных лет, содержащихся в пределах до 1643 г. Для этого 1642 делим на 4. У нас получается 410. Остаток отбрасываем: он значения не имеет. Наконец, высчитываем количество полных дней в текущем (1643) году до наступления указанного в источнике числа месяца -- 3 апреля. Прошло три месяца: январь (31 день), февраль (28 дней, т. к. год простой), март (31 день) и два дня (апрельских), -- всего 92 дня. Сумма трех слагаемых (1642, 410 и 92) дает 2144. Делим эти сумму на 7. Частное -- 306, остаток -- 2. В конечном итоге для нас представляет интерес именно остаток, он указывает, на какой по порядку день недели падает 3 апреля 1643 г. Очевидно, -- на второй день, каковым, как мы знаем, эта формула предполагает понедельник.
        Надо учесть еще то обстоятельство, что суббота является седьмым днем, но остатка в 7 единиц при делителе, равном 7, получиться никак не может. Очевидно, в том случае, когда искомым днем недели служит суббота, деление должно произойти без остатка.

 Таблица X

Определение дня недели

Числа месяцев

Дни недели

 

3.10.17.24.31

7.14.21.28

4.11.18.25 

1.8.15.22.29

5.12.19.26

 2.9.16.23.30

6.13.20.27

Воскресенье

Понедельник

Вторник

Среда

Четверг

Пятница

Суббота

4.11.18.25

1.8.15.22.29

5.12.19.26 

 2.9.16.23.30

6.13.20.27

6.13.20.27 

7.14.21.28

Понедельник

 Вторник

Среда

Четверг

Пятница

Суббота

Воскресенье

5.12.19.26 

 2.9.16.23.30

6.13.20.27 

3.10.17.24.31

7.14.21.28

7.14.21.28

1.8.15.22.29

Вторник

Среда

Четверг

Пятница

Суббота

Воскресенье

Понедельник

6.13.20.27 

3.10.17.24.31 

 7.14.21.28

4.11.18.25 

1.8.15.22.29

1.8.15.22.29

 2.9.16.23.30

Среда

Четверг

Пятница

Суббота

Воскресенье

Понедельник

Вторник

 7.14.21.28

 4.11.18.25

 1.8.15.22.29

5.12.19.26

 2.9.16.23.30

 2.9.16.23.30

3.10.17.24.31

Четверг

Пятница

Суббота

Воскресенье

Понедельник

Вторник

Среда

1.8.15.22.29

 5.12.19.26

 2.9.16.23.30

6.13.20.27 

3.10.17.24.31

3.10.17.24.31

4.11.18.25 

Пятница

Суббота

Воскресенье

Понедельник

Вторник

Среда

Четверг

 2.9.16.23.30

6.13.20.27 

3.10.17.24.31

7.14.21.28

4.11.18.25

4.11.18.25 

5.12.19.26

Суббота

Воскресенье

Понедельник

 Вторник

Среда

Четверг

Пятница

Месяцы мартовского стиля

А

В

Г

Д

Е

S

З

 Мартовский
стиль

 Март
Ноябрь

Апрель
Июль

Август

Сентябрь
Декабрь

Май
Январь

Июнь
Февраль

Октябрь 

При вруцелете

 

 Месяцы январского стиля

 

 Январский
стиль

 Март
Ноябрь

Апрель
Июль

 Август

Сентябрь
Декабрь

Май

Июнь

Октябрь

 Простой

Февраль

 

 

 

 

 

Январь

Високосный

 

Январь

Февраль

 

 

 

 

 

 Месяцы сентябрьского стиля

Сентябрьский
стиль

Март

Апрель
Июнь

Август

 

Май

Июнь

 

 Простой

Февраль

Октябрь

Ноябрь

 

 

Сентябрь
Декабрь

Январь

Високосный

Сентябрь
Декабрь

Январь

Февраль

Октябрь

Ноябрь

 

 

-46-

        Несколько иной вариант той же самой формулы выработал известный ученый Карский. В силу видоизменений, внесенных последним в формулу Перевощикова, она приобрела следующий вид:
        X=[N + 14(N - l) + T + 5] : 7
        Значение букв в данном случае остается таким же, как и в предыдущем. Но, как мы видим, в противоположность Перевощикову, Карский, в качестве первого слагаемого берет цифровое обозначение текущего года, а не число предшествующих ему лет, а в качестве второго слагаемого -- количество дней, прошедших от начала текущего года до искомой даты, включая сюда и день, подлежащий определению. В результате подобных поправок, сумма трех основных слагаемых оказывается большей на 2 единицы, по сравнению с вычислениями Перeвощикова. Следовало как-то добиться, чтобы эти лишние единицы не отразились на остатке от последующего деления указанной суммы на 7. Это достигается прибавлением к подлежащему делению числу еще 5 единиц. 5 + 2 дают и сумме число 7, которое делится на 7 без остатка. Тем самым парализуется возможность увеличения остатка, на две единицы, и вое дальнейшие вычисления Перевощикова остаются в силе.
        Проверим предшествующий пример, руководствуясь формулой Карского:
        N=1643; 14 (N - 1) = 410; Т = 93.
        X = остатку от деления (1643 + 410 + 93 + 5) : 7 = остатку от деления 2151 на 7.
        Частное от деления 2151 на 7 равно 307. Остаток = 2. Второй день недели -- понедельник.
        Автором третьего способа определения дня недели является исследователь Черухин. Он прежде всего предлагает цифровое обозначение данного года по эре от "рождества христова" умножить на 5, а полученное произведение разделить на 4. Берется частное, а остаток в расчет не принимается. Далее Черухин приводит последовательный ряд цифр в количестве 12-ти: 400351362402. Каждая из этих цифр соответствует одному из 12 месяцев простого года, расположенных в порядке их чередования. Для месяцев високосного года Черухин предусматривает некоторые изменения в отношении января и февраля. Именно, январю соответствует не 4, а 3, февралю, -- не 0, а 6. Остальные цифры остаются в силе и при действиях с високосными годами. В зависимости от того, какой месяц фигурирует в подлежащей определению дате, соответствующая ему цифра прибавляется к частному, полученному, как говорилось, от деления на 4 цифрового обозначения года, предварительно умноженного на 5. К полученному результату прибавляется еще число месяца. А затем уже вся сумма делится на 7. Остаток от деления укажет на порядковый номер дня недели, при чем в отличие от Перевощикова и Карского, счет начинаетя не с воскресенья, а с понедельника: первый день недели -- понедельник, седьмой -- воскресенье. При отсутствии остатка, порядковый номер дня недели равен делителю, т. е. 7, и

-47-

таким образом, определяемым днем является в этом случае воскресенье.
        Способ Черухина может быть выражен в виде следующей, формулы:
        X = остатку от деления выражения [(5N : 4) + М + Т] : 7.
        X -- порядковый номер дня недели, считая первым понедельник, седьмым -- воскресенье; N -- цифровое обозначение данного года; М -- цифра, соответствующая в приведенном Черухиным ряду данному месяцу; Т -- указанное число месяца.
        Вернемся еще раз к той задаче то определению дня недели, которую мы решали, пользуясь формулами Перевощикова и Карского. Применим к ней способ Черухяна:
        5N : 4= 1643 х 5 : 4 = 8215 : 4 = 2053; M = 3; Т = 3; 2053 + 3 + 3 = 2059; 2059 : 7 = 294 и 1 в остатке. Первый день недели, по формуле Черухина, -- понедельник.
        Выше было уже отмечено, что все три рассмотренные нами формулы разработаны применительно к датам нашего летосчисления. Если же нам приходится иметь дело с датами от "сотворения мира", то в этом случае, очевидно, предварительно следует перевести их на эру от "рождества христова".
         § 14. Сутки и их деление. В древнерусских источниках отсутствует, термин "сутаси". Вместо последнего употреблялось слово "день". При этом день (в значении суток) делился на две части (светлую и темную): день в собственном смысле слова и ночь.
        Трудно точно установить, когда иа Руси вошло в обиход измерение времени часами. В древних источниках слово "час" часто встречается не только в смысле единицы времени (= 124 суток), a в значении неопределенного момента (например, "смертный час"). Но наряду с этим в целом ряде источников мы находим, 24-часовое деление суток. Каждый час содержал в себе 6 "дробных часовцев" или 60 "чаcцев". Таким образом, часец означает минуту. Существовали издавна и приборы для измерения времени. Уже от начала XV в. до нас дошло первое описание механических часов: "Великий князь задумал устроить часник и подставил его на своем дворе за церковью св. благовещения. Этот часник носил название часомерия (прибора для измерения часов). Каждый час происходил удар молота в колокол, размерявший и рассчитывавший часы ночные и дневные. Не человек ударял, но как бы рукою человека сам собою совершался эвон. Это было устроено при помощи чело-веческого разума, в высшей степени искусно и хитро". Мастером и художником, создавшим этот прибор, был сербский выходец, -- монах по имени Лазарь. Цена "чаcника" превышала 150 рублей.
        Знакомство с системой древне-русского счета часов необходимо потому, что она отличалась от принятой в наше время и в силу этого имеющиеся в источниках указания на части суток требуют перевода на соответственные им часы, согласно современному делению суток.
        При суточном измерении времени в древней Руси люди исходили из наблюдений над естественной сменой дня и ночи и приводили их в связь с часами церковных богослужений.

-48-

        Сутки начинались не в полночь, как это принято теперь, а в период вставания людей от сна и обращения к обычной деятельности. Это совпадало с утренним богослужением ("заутреней"), которое начиналось еще перед зарей и оканчивалось до восхода солнца. Князь XII в. Владимир Мономах писал в "Поучении" своим детям: "Пусть не застанет вас солнце в постели. Так делал мой отец и все добрые мужи: отдав богу заутреннюю хвалу, и после солнечного восхода увидев солнце и прославив бога с радостью, открывал совет с дружиной, или судил людей, или ехал на охоту...". Таким образом, с первого часа дня (по древне-русскому счету) люди обращались к своим очередным делам. Время от 3 часов до "полудня" -- период "обеда". В этот период в церкви служилась "обедня". "Полдень" наступал в 6-7 часов. До захода солнца происходила очередная церковная служба -- "вечерня", причем время дня после "вечерни" примыкало к вечеру. Ночь тянулась от конца сумерек до первых признаков зари.
        В древне-русских источниках время, на которое приходится то или иное событие, часто указывается не в часах, а в церковных службах. Поэтому необходимо было иа них остановиться.
        В церковных календарях распределение "дневных" и "ночных" часов было неодинаковым для различных месяцев, а также их подразделений. Если в нашем быту день приравнивается условно ночи в течение всего года (12 час. + 12 час.), а счет часов ведется сплошной (1 -- 24), то в древней Руси, в зависимости от того или иного числа и месяца, продолжительность дня (а соответственно и ночи) колебалась от 7 до 17 часов. Эти колебания зависели от естественной смены темной и светлой частей суток а связи со сменой природных явлений.
        Соответствие часов по древне-русскому измерению времени, принятому в XVI-XVII вв., и позднейшему исчислению (XIX в.) приводится в таблице XI.
        При пользовании таблицей числа месяцев мадо искать в следующем порядке (соответствующем их последовательности в пределах календарного года): начиная со второй графы (внизу) -- вправо до конца таблицы, затем поднявшись вверх, с крайней графы -- влево до конца таблицы.
        При пользовании источниками следует учитывать, что в ряде областей (например, в Новгороде) счет часов отличался от московского. Но останавливаться на этих местных рсобенностях мы не будем.
         § 15 Датировка по непереходящим праздникам. Очень часто источники, приводя дату какого-либо исторического события, вместо указания месяца и числа, ограничиваются ссылкой на церковный праздник, случайно с этим событием совпавший. При общем религиозном характере древне-русской письменности такая система датировки была понятна читателям и не требовала комментариев. Но современному исследователю в этом случае, в целях уточнения даты, приходится по празднику определять соответствующее ему число. Русский церковный календарь различал среди праздников непереходящие (неподвижные) и переходящие

-49-

 Таблица XI

Суточный счет часов

27 ноября - 
1 января

11 ноября - 26 ноября

26 ноября - 10 ноября

10 октября -
25 октября

24 сентября -
9 октября

8 сентября -
23 сентября

23 августа -
7 сентября

7 августа -
22 августа

23 июля -
6 августа

6 июля -
22 июля

25 мая -
5 июля

Часы
древ.

Их нач. по сов. сч.

Часы
древ.

Их нач. по сов. сч.

Часы
древ.

Их нач. по сов. сч.

Часы
древ.

Их нач. по сов. сч.

Часы
древ.

Их нач. по сов. сч.

Часы
древ.

Их нач. по сов. сч.

Часы
древ.

Их нач. по сов. сч.

Часы
древ.

Их нач. по сов. сч.

Часы
древ.

Их нач. по сов. сч.

Часы
древ.

Их нач. по сов. сч.

Часы
древ.

Их нач. по сов. сч.

1ч.д.

8,5

1ч.д.

7,35

1ч.д.

7,5

1ч.д.

6,35

1ч.д.

6,5

1ч.д.

5,35

1ч.д.

5,5.

1ч.д.

4,35

1ч.д.

4,5

1ч.д.

3,35

1ч.д.

3,5

2

9,5

2

8,35

2

8,5

2

7,35

2

7,5

2

6,35

2

6.5

2

5,35

2

5,5

2

4,35

2

4,5

3

10,5

3

9,35

3

9,5

3

8,35

3

8,5

3

7,35

3

7,5

3

6,35

3

6,5

3

5,35

3

5,5

4

11,5

4

10,35

4

10,5

4

9,35

4

9,5

4

8,35

4

8,5

4

7,35

4

7,5

4

6,35

4

6,5

5

12,5

5

11,35

5

11,5

5

10,35

5

10,5

5

9,35

5

9,5

5

8,35

5

8,5

5

7,35

5

7,5

6

13,5

6

12,35

6

12,5

6

11,35

6

11,5

6

10,35

6

10,5

6

9,35

6

9,5

6

8,35

6

8,5

7

14,5

7

13,35

7

13,5

7

12,35

7

12,5

7

11,35

7

11,5

7

10,35

7

10,5

7

9,35

7

9,5

1ч.н.

15,5

8

14,35

8

14,5

8

13,35

8

13,5

8

12,35

8

12,5

8

11,35

8

11,5

8

10,35

8

10,5

2

16,5

1ч.н.

15,35

9

15,5

9

14,35

9

14,5

9

13,35

9

13,5

9

12,35

9

12,5

9

11,35

9

11,5

3

17,5

2

16,35

1ч.н.

16,5

10

15,35

10

15,5

10

14,35

10

14,5

10

13,35

10

13,5

10

12,35

10

12,5

4

18,5

3

17,35

2

17,5

1ч.н.

16,35

11

16,5

11

15,35

11

15,5

11

14,35

11

14,5

11

13,35

11

13,5

5

19,5

4

18,35

3

18,5

2

17,35

1ч.н.

17,5

12

16,35

12

16,5

12

15,35

12

15,5

12

14,35

12

14,5

6

20,5

5

19,35

4

19,5

3

18,35

2

18,5

1ч.н.

17,35

13

17,5

13

16,35

13

16,5

13

15,35

13

15,5

7

21,5

6

20,35

5

20,5

4

19,35

3

19,5

2

18,35

1ч.н.

18,5

14

17,35

14

17,5

14

16,35

14

16,5

8

22,5

7

21,35

6

21,5

5

20,35

4

20,5

3

19,35

2

19,5

1ч.н.

18,35

15

18,5

15

17,35

15

17,5

9

23,5

8

22,35

7

22,5

6

21,35

5

21,5

4

20,35

3

20,5

2

19,35

1ч.н.

19,5

16

18,35

16

18,5

10

0,5

9

23,35

8

23,5

7

22,35

6

22,5

5

21,35

4

21,5

3

20,35

2

20,5

1ч.н.

19,35

17

19,5

11

1,5

10

0,35

9

0,5

8

23,35

7

23,5

6

22,35

5

22,5

4

21,35

3

21,5

2

20,35

1ч.н.

20,5

12

2,5

11

1,35

10

1,5

9

0,35

8

0,5

7

23,35

6

23,5

5

22,35

4

22,5

3

21,35

2

21,5

13

3,5

12

2,35

11

2,5

10

1,35

9

1,5

8

0,35

7

0,5

6

23,35

5

23,5

4

22,35

3

22,5

14

4,5

13

3,35

12

3,5

11

2,35

10

2,5

9

1,35

8

1,5

7

0,35

6

0,5

5

23,35

4

23,5

15

5,5

14

4,35

13

4,5

12

3,35

11

3,5

10

2,35

9

2,5

8

1,35

7

1,5

6

0,35

5

0,5

16

6,5

15

5,35

14

5,5

13

4,35

12

4,5

11

3,35

10

3,5

9

2,35

8

2,5

7

1,35

6

1,5

17

7,5

16

6,35

15

6,5

14

5,35

13

5,5

12

4,35

11

4,5

10

3,35

9

3,5

8

2,35

7

2,5

27 ноября - 
1 января

2 января -
16 января

17 января -
1 февраля

2 февраля -
17 февраля

18 февраля -
5 марта

6 марта -
20 марта

21 марта -
5 апреля

6 апреля -
22 апреля

23 апреля -
8 мая

9 мая -
24 мая

25 мая -
5 июля

-50-

(подвижные). Первые приходятся ежегодно на одни и те же определенные числа. Вторые не имеют постоянных дат и в разные годы падают на различные числа.
        Наименьшие трудности представляют для исследователя, конечно, неподвижные праздники. Если историк захочет произвести по ним датировку интересующего его события, то ему достаточно заглянуть в любой русский дореволюционный календарь, где он найдет точные указания в отношении церковных праздников. К числу неподвижных праздников, наиболее часто встречающихся в источниках, принадлежат (в порядке древне-русского сентябрьского года): "Семень день Летоначатца" или "Семень деиь Летопроводц" -- день нового года -- 1 сентября; рождество богородицы -- 8 сентября; покров богородицы -- 1 октября; выведение во храм богородицы -- 21 ноября; Николин день осенний или зимний --6 декабря; рождество Христово -- 25 декабря; крещение -- 6 января; сретение -- 2 февраля; благовещение -- 26 марта; преображение -- 6 августа; Никелин день (весенний -- 9 мая; успенье или госпожин (оспожин) день -- 15 августа и т. д. Но вообще говоря, каждый день в церковном календаре связан с памятью какого-либо святого, и древне-русские источники, особенно летописи, поэтому пестрят указаниями подобного рода: "такого-то числа, на память такого-то святого". Некоторые из этих дат, помимо чисто церковного назначения, имели большое значение и в гражданском быту, например, знаменитый Юрьев день (осенний -- 26 ноября, весенний -- 23 апреля), сыгравший такую серьезную роль в развитии крестьянской крепости. Часто попадаются в источниках ссылки и на тот или иной пост, говоря древне-русским языком, -- "говейно" или "говение": Петров пост (конч. 29 июня), успенский (с 1 августа и до успения), Филиппов или рождественский (с 15 ноября и до рождества) и т. д. Как уже было сказано, за всеми справками в отношении такого рода данных, встречающихся в документах, надлежит обращаться к старым календарям.
         § 16. Основы пасхалии. Несколько сложнее обстоит дело в том случае, когда мы встречаем в источниках датировки посредством ссылки на переходящие (подвижные) праздники или вообще церковные даты (например, посты), падающие в различные годы на разные числа. Надо прежде всего знать, что все подвижные праздники и посты зависят от пасхи, будучи отделены от нее постоянными сроками. Поэтому при установлении любой подвижной церковной даты необходимо предварительно вычислить, когда в интересующем нас году приходится пасха. А затем, зная на сколько дней до или после пасхи наступает упоминающийся в источниках зиаменательный для церкви передвижмой день церковного календаря, мы уже легко выясняем дату последнего.
        Вычисление дня празднования православной пасхи в любом году производится церковниками довольно сложными методами. Нам нет надобности на них останавливаться подробно. Историки подходят к этому вопросу чисто практически. Они исходят в своей работе из результатов, полученных богословами, и пользуются выработанными ими формулами и таблицами (для основной

-51-

научной цели -- расшифровки хронологических данных, встречающихся в древне-русских документах. Надо только отметить, что подвижность пасхи объясняется тем обстоятельством, что пасхальные даты -- это даты лунного календаря, не совпадающего с солнечным (Юлианским).
        В основе пасхалии (так принято называть весь комплекс вопросов, связанных с определением пасхи) лежит следующая предпосылка: пасха должна праздноваться в первое воскресенье после весеннего полнолуния. А весенним считается полнолуние, которое бывает не ранее 21 марта и не позднее 18 апреля. Ведь мы знаем, что солнечный год (= около 365,25 суток) не содержит в себе полного количества лунных месяцев (=29,5306 суток), вследствие чего фазы луны приходятся в различные годы на разные числа месяцев. Поскольку за наиболее раннюю дату весеннего полнолуния церковь принимает 21 марта, постольку, очевидно самым ранним днем празднования пасхи может быть 22 марта (если это число совпадет с воскресеньем). А наиболее поздней пасхальной датой будет воскресенье 25 апреля, т. к. это самое позднее (из возможных) воскресенье, следующее за последним (из установленных богословами) днем весеннего полнолуния. Период времени с 22 марта по 25 апреля включительно называется "пасхальным пределом". Это название принято потому, что день празднования пасхи из года в год передвигается (в определенном порядке) только в указанных rpaницах, не выходя из них.
         § 17. Метонов (лунный) цикл. При вычислении пасхи церковники руководствуются астрономическими данньми, именно, наблюдениями над периодической сменой лунных фаз. Уже не раз говорилось о том, что фазы луны не могут приходиться ежегодно на постоянные числа. Но через каждые 19 лет наблюдается повторение лунных фаз в одни и те же дни солнечного календаря. Это происходит потому, что 19 солнечных лет содержат в себе 235 полных лунных месяцев. Следовательно, через 19-летний период луна как бы завершает свой круг и возвращается к исходной точке солнечного календаря. Действительно, 19 солнечных лет = 365,25 суток х 19=6939,75 суток. В переводе на лунный календарь это даст 235 месяцев (6939,75:29,5306=235). Значение, 19-летнего цикла (называемого "лунным") для установления соответствия между солнечным и лунным календарным счетом было вскрыто очень давно, еще в V в. до н. э., греческим астрономом Метоном. По имени последнего лунный цикл именуется иногда также Метоновым циклом.
         § 18. Золотые числа. Древние римляне использовали наблюдение Метона для вычисления дат новолуний и полнолуний, в связи с которыми они совершали свои жертвоприношения. Каждому году в пределах текущего 19-летия они решили дать свой порядковый номер. Для этого необходимо было Метонов цикл привести в определенную связь с Юлианским календарем. По ряду соображений (отнюдь не научного характера, на которых останавливаться здесь нет надобности), было признано, что 1-ый год по "рождества христове" являлся вторым в лунном цикле. И на этой основе

-52-

был построен дальнейший счет. Порядковый номер N-oro года внутри незавершенного текущего девятнадцатилетнего периода получил название "золотого числа", т. к. оно (число) писалось золотыми буками на доске, выставляемой для всеобщего сведения. Из изложенного выше очевидно, что для вычисления золотого числа необходимо к цифровому обозначению интересующего нас года прибавить единицу, полученную сумму разделить на 19 и взять остаток от этого деления. Золотое число 1643 года = 10, т. к. остаток от (деления (1643+1) на 19 будет 10.
         § 19. Круги луны. В древне-русской (византийской) хронологии вычисление порядкового номера года (называвшегося "кругом луны") в девятнадцатилетнем лунном цикле было построено на несколько ином принципе. Поскольку от "сотворения мира" до "рождества христова" считалось 5508 лет, постольку 1-ый год до "рождества христова" был 17-м по счету в 290-м незаконченном цикле луны (5508 : 19 = 289 и 17 в остатке). Следовательно, круг луны 1-го года н. э. = 18; 2-го года = 19; 3-го года = 1 и т. д. А золотое число 3-го года н. э. = 4. Отсюда ясно, что расхождение между золотым числом и кругом луны любого года выражается, в цифре 3. Раз золотое число 1643 года =10, то его круг луны = 7. Поэтому, если для вычисления золотого числа, мы предварительно цифровое обозначение даты нашей эры увеличиваем на единицу, а затем, уже делим на 19, то для определения круга луны, наоборот прибегаем сначала к вычитанию двух единиц (учитывая, что круг луны N-oro года на 3 меньше его золотого числа). Следовательно, круг луны 1643 г. = остатку от деления (1643 - 2) на 19 = 7. Если дата дана по византийской эре, то достаточно просто разделить ее на 19 и остановиться на остатке от этого деления. Круг луны 6746 г = 1 (6746 : 19 = 355 и 1 в остатке).
        Для определения круга луны можно также воспользоваться специальной таблицей XII.
        Таблица построена по той же системе, что и большинство предыдущих. Круг луны данного года находится на пересечении вертикальный и горизонтальной линий, проведенных сверху вниз и слева направо от цифр тысячелетий и столетий -- с одной стороны, и цифр десятилетий и единиц лет -- с другой.
         § 20. Вычисление пасхи по кругу луны, кругу солнца и вруцелету. Совершенно очевидно, что дата празднования пасхи в том или ином году находится в прямой зависимости от круга луны последнего (или от тесно связанного с кругом луны золотого числа), т. к. в каждое девятнадцатилетне весеннее полнолуние, определяющее пасху, падает на одно и то же число. Но с другой стороны ведь пасха зависит не только от даты весеннего полнолуния, но и от того, когда придется ближайшее к нему воскресенье. А дни недели, как мы знаем, также передвигаются по числам солнечного календаря, и порядок этого передвижения повторяется через 28 лет. Поэтому для вычисления пасхи надо еще знать порядковое место года в пределах 28-летнего цикла (круг

-53-

 Таблица XII

Круги луны

Десятки и единицы
годов

\

Тысячи и сотни
годов

От сотв.
мира

6100

6200

6300

6400

6500

6600

6700

6800

6900

7000

7100

7200

7300

7400

7500

 

 

 

 

От сотв.
мира

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5600

5700

5800

5900

6000

От рожд.
христ.

1200

1300

1400

1500

1600

1700

1800

1900

2000

 

 

 

 

 

 

 

 

 

 

От рожд. 
христ.

 

 

 

 

 

 

 

0

100

200

300

400

500

600

700

800

900

1000

1100

0. 19. 38. 57. 76 .95

1

6

11

16

2

7

12

17

3

8

13

18

4

9

14

19

5

10

15

к
р
у
г
и

л
у
н
ы

1. 20. 39. 58. 77. 96

2

7

12

17

3

8

13

18

4

9

14

19

5

10

15

1

6

11

16

2. 21. 40. 59. 78. 97

3

8

13

18

4

9

14

19

5

10

15

1

6

11

16

2

7

12

17

3. 22. 41. 60. 79. 98

4

9

14

19

5

10

15

1

6

11

16

2

7

12

3

3

8

13

18

4. 23. 42. 61. 80. 99

5

10

15

1

6

11

16

2

7

12

17

3

8

13

17

4

9

14

19

5. 24. 43. 62. 81

6

11

16

2

7

12

17

3

8

13

18

4

9

14

18

5

10

15

1

6. 25. 44. 63. 82

7

12

17

3

8

13

18

4

9

14

19

5

10

15

19

6

11

16

2

7. 26. 45. 64. 83

8

13

18

4

9

14

19

5

10

15

1

6

11

16

1

7

12

17

3

8. 27. 46. 65. 84

9

14

19

5

10

15

1

6

11

16

2

7

12

17

2

8

13

18

4

9. 28. 47. 66. 85

10

15

1

6

11

16

2

7

12

17

3

8

13

18

3

9

14

19

5

10. 29. 48. 67. 86

11

16

2

7

12

17

3

8

13

18

4

9

14

19

4

10

15

1

6

11. 30. 49. 68. 87

12

17

3

8

13

18

4

9

14

19

5

10

15

1

5

11

16

2

7

12. 31. 50. 69. 88

13

18

4

9

14

19

5

10

15

1

6

11

16

2

6

12

17

3

8

13. 32. 51. 70. 89

14

19

5

10

15

1

6

11

16

2

7

12

17

3

7

13

18

4

9

14. 33. 52. 71. 90

15

1

6

11

16

2

7

12

17

3

8

13

18

4

8

14

19

5

10

15. 34. 53. 72. 91

16

2

7

12

17

3

8

13

18

4

9

14

19

5

9

15

1

6

11

16. 35. 54. 73. 92

17

3

8

13

18

4

9

14

19

5

10

15

1

6

10

16

2

7

12

17. 36. 55. 74. 93

18

4

9

14

19

5

10

15

1

6

11

16

2

7

11

17

3

8

13

18. 37. 56. 75. 94

19

5

10

15

1

6

11

16

2

7

12

17

3

8

12

18

4

9

14

-54-

солнца) 1). Наконец, выше указывалось на тесную связь круга солнца и вруцелета. Вот эти три величины (круг луны, круг солнца и вруцелето данного года) и являются а конечном итоге решающими при вычислении пасхи. На их основе и строятся специальные таблицы.
        Ниже приводится таблица XIII для определения пасхи путем сочетания найденных предварительно круга луны и вруцелета 2).

 Таблица XIII

Определение пасхи (по кругу луны и вруцелету)

Пасха

Вруцелета

Круги луны

    22 марта

Г

 

 

 

 

13

 

    23

В

2

 

 

 

13

 

    24

А

2

 

 

 

13

 

    25

З

2

 

 

10

13

 

    26

S

2

 

 

10

13

18

    27

Е

2

 

 

10

13

18

    28

Д

2

 

7

10

13

18

    29

Г

2

 

7

10

 

18

    30

В

 

 

7

10

15

18

    31

А

 

4

7

10

15

18

    1 апреля

З

 

4

7

 

15

18

    2

S

 

4

7

12

15

 

    3

Е

1

4

7

12

15

 

    4

Д

1

4

 

12

15

 

    5

Г

1

4

9

12

15

 

    6

В

1

4

9

12

 

17

    7

А

1

 

9

12

 

17

    8

З

1

6

9

12

 

17

    9

S

1

6

9

 

 

17

    10

Е

 

6

9

 

14

17

    11

Д

3

6

9

 

14

17

    12

Г

3

6

 

 

14

17

    13

В

3

6

 

11

14

 

    14

А

3

6

 

11

14

19

    15

З

3

 

 

11

14

19

    16

S

3

 

8

11

14

19

    17

Е

3

 

8

11

 

19

    18

Д

 

 

8

11

16

19

    19

Г

 

5

8

11

16

19

    20

В

 

5

8

 

16

19

    21

А

 

5

8

 

16

 

    22

З

 

5

8

 

16

 

    23

S

 

5

 

 

16

 

    24

Е

 

5

 

 

16

 

    25

Д

 

5

 

 

 

 

        ___________
        1) О том, как находить круг солнца, рассказано в § 11.
        2) См. § 12

-55-

        День празднования пасхи лежит на линии, пересекающей одновременно и вруцелето и круг луны N-ого года.
        В основу другого способа определения пасхи кладутся сразу три величины (круг луны, круг солнца и вруцелето). Для пользования таблицей XIV, из этих трех величин достаточно знать только две (обязательно круг луны и на выбор: или круг солнца, или вруцелето). Линии, проведенные сверху вниз (от круга солнца или вруцелета) и слева направо (от круга луны), встретившись, укажут день празднования пасхи.
         § 21. Великий индиктион. Наконец, для определения пасхи можно (пользоваться таблицей так называемого "обращения великого индиктиона". Под великим индиктионом имеется в виду порядковый номер года в пределах периода в 532 года 1). Цифра 532 получается в результате умножения 28 (солнечный цикл) на 19 (лунный цикл). Мы знаем, что Наблюдается определенный порядок в передвижении дня пасхи по числам календаря. Этот порядок повторяется каждые 532 года. Счет индиктионами ведется от "сотворения мира". Но в печатаемой ниже таблице XV приведены годы по нашему летосчислению, причем начиная с 13 индиктиона, т. е. с конца IX века. Более ранние даты в русских источниках не встречаются. Против каждого года (по эре от "рождества христова") прямо указан день пасхи без всяких вычислений. С конца IX в. до нашего времени прошло всего два индиктиона (13-й и 14-й), так что таблица включает только два столбца цифр и ориентироваться в них, конечно, не представляется никакой трудности.
        Если дата дана в источниках по византийскому летосчислению, то требуется ее предварительно перевести иа нашу эру. Никаких сомнений при переводе в смысле выяснения календарного стиля не возникает, т.к. пасха ведь приходится только на один из двух возможных месяцев (март и апрель), для которых при любом стиле вычитаемым служит число 5508.
         § 22. Формула Гауса. Наконец, вычислить пасху можно и минуя таблицы, на основании особой формулы, предложенной более ста сорока лет тому назад, немецким математиком Гаусом. Эта формула не была доказана ее автором и получила доказательство уже много позднее, в 1870 г., в трудах профессора Базельского университета Германа Кинкелина. Мы, историки, имеем право не вдаваться детально в значение отдельных, приводимых Гаусом, математических выражений. Мы должны взять эти выражения в готовом виде и воспользоваться ими в тех случаях, когда они могут помочь нашему пониманию древне-русских дат.
        Основная формула Гауса была выработана для определения Григорианской пасхи, т. е. пасхи, празднуемой Западной церковью, которая пользовалась Григорианским календарем. Но с внесением известных поправок формула эта вполне применима и для установления православной Юлианской пасхи, которую имеют в виду
        ___________
        1) Не надо путать с индиктом, под которым, как указано выше (§ 7) понимается порядковый номер года в текущем пятнадцатилетии.

-56-

 Таблица XIV

Определение пасхи (по кругу солнца, кругу луны и вруцелету)

Круги
луны

Вруцелета

А

В

Г

Д

Е

S

З

Круги солнца

1

2

3

-

4

5

6

7

-

8

9

10

11

-

12

13

14

15

-

16

17

18

19

-

20

21

22

23

-

24

25

26

27

-

28

 

1

7

6

5

4
апреля

3

9

8

2

24

23

29

28
марта

27

26

25

3

14

13

12

11
апреля

17

16

15

4

31
марта

6

5

4
апреля

3

2

1

5

21

20

19

25
апреля

24

23

22

6

14

13

12

11
апреля

10

9

8

7

31

30

29
марта

28

3

2
апреля

1

8

21

20

19

18
апреля

17

16

22

9

7

6

5

11
апреля

10

9

8

10

31

30

29

28
марта

27

26

25

11

14

13

19

18
апреля

17

16

15

12

7

6

5

4
апреля

3

2

8

13

24

23

22

28
марта

27

26

25

14

14

13

12

11
апреля

10

16

15

15

31

30
марта

5

4

3
апреля

2

1

16

21

20

19

18
апреля

24

23

22

17

7

6

12

11
апреля

10

9

8

18

31

30

29

28
марта

27

26

25

19

14

20

19

18
апреля

17

16

15

-57-

 Таблица XV

Обращение великого индиктиона (а=апрель, м=март)

NN
года
текущ.
инд-на

Индиктионы

Пасха

NN
года
текущ.
инд-на

Индиктионы

Пасха

NN
года
текущ.
инд-на

Индиктионы

Пасха

NN
года
текущ.

инд-на 

Индиктионы

Пасха

NN
года
текущ.

инд-на

Индиктионы

Пасха

NN
года
текущ.

инд-на

Индиктионы

Пасха

13

14

13

14

13

14

13

14

13

14

13

14

1

877

1409

7 а

46

922

1454

21 а

91

967

1499

31 м

136

1012

1544

13 а

181

1057

1589

30 м

226

1102

1634

6 а

2

878

1410

23 м

47

923

1455

6 а

92

968

1500

19 а

137

1013

1545

5 а

182

1058

1590

19 а

227

1103

1635

29 м

3

879

1411

12 а

48

924

1456

28 м

93

969

1501

11 а

138

1014

1546

25 а

183

1059

1591

4 а

228

1104

1636

17 а

4

880

1412

3 а

49

925

1457

17 а

94

970

1502

27 м

139

1015

1547

10 а

184

1060

1592

26 м

229

1105

1637

9 а

5

881

1413

23 а

50

926

1458

2 а

95

971

1503

16 а

140

1016

1548

1 а

185

1061

1593

15 а

230

1106

1638

25 м

6

882

1414

8 а

51

927

1459

25 м

96

972

1504

7 а

141

1017

1549

21 а

186

1062

1594

31 м

231

1107

1639

14 а

7

883

1415

31 м

52

928

1460

13 а

97

973

1505

23 м

142

1018

1550

6 а

187

1063

1595

20 а

232

1108

1640

5 а

8

884

1416

19 а

53

929

1461

5 а

98

974

1506

12 а

143

1019

1551

29 м

188

1064

1596

11 а

233

1109

1641

25 а

9

885

1417

11 а

54

930

1462

18 а

99

975

1507

4 а

144

1020

1552

17 а

189

1065

1597

27 м

234

1110

1642

10 а

10

886

1418

27 м

55

931

1463

10 а

100

976

1508

23 а

145

1021

1553

2 а

190

1066

1598

16 а

235

1111

1643

2 а

11

887

1419

16 а

56

932

1464

1 а

101

977

1509

8 а

146

1022

1554

25 м

191

1067

1599

8 а

236

1112

1644

21 а

12

888

1420

7 а

57

933

1465

14 а

102

978

1510

31 м

147

1023

1555

14 а

192

1068

1600

23 м

237

1113

1645

6 а

13

889

1421

23 м

58

934

1466

6 а

103

979

1511

20 а

148

1024

1556

5 а

193

1069

1601

12 а

238

1114

1646

29 м

14

890

1422

12 а

59

935

1467

29 м

104

980

1512

11 а

149

1025

1557

18 а

194

1070

1602

4 а

239

1115

1647

18 а

15

891

1423

4 а

60

936

1468

17 а

105

981

1513

27 м

150

1026

1558

10 а

195

1071

1603

24 а

240

1116

1648

2 а

16

892

1424

23 а

61

937

1469

2 а

106

982

1514

16 а

151

1027

1559

26 м

196

1072

1604

8 а

241

1117

1649

25 м

17

893

1425

8 а

62

938

1470

22 а

107

983

1515

8 а

152

1028

1560

14 а

197

1073

1605

31 м

242

1118

1650

14 а

18

894

1426

31 м

63

939

1471

14 а

108

984

1516

23 м

153

1029

1561

6 а

198

1074

1606

20 а

243

1119

1651

30 м

19

895

1427

20 а

64

940

1472

29 м

109

985

1517

12 а

154

1030

1562

29 м

199

1075

1607

5 а

244

1120

1652

18 а

20

896

1428

4 а

65

941

1473

18 а

110

986

1518

4 а

155

1031

1563

11 а

200

1076

1608

27 м

245

1121

1653

10 а

21

897

1429

27 м

66

942

1474

10 а

111

987

1519

24 а

156

1032

1564

2 а

201

1077

1609

16 а

246

1122

1654

26 м

22

898

1430

16 а

67

943

1475

26 м

112

988

1520

8 а

157

1033

1565

22 а

202

1078

1610

8 а

247

1123

1655

15 а

23

899

1431

1 а

68

944

1476

14 а

113

989

1521

31 м

158

1034

1566

14 а

203

1079

1611

24 м

248

1124

1656

6 а

24

900

1432

20 а

69

945

1477

6 а

114

990

1522

20 а

159

1035

1567

30 м

204

1080

1612

12 а

249

1125

1657

29 м

25

901

1433

12 а

70

946

1478

22 м

115

991

1523

5 а

160

1036

1568

18 а

205

1081

1613

4 а

250

1126

1658

11 а

26

902

1434

28 м

71

947

1479

11 а

116

992

1524

27 м

161

1037

1569

10 а

206

1082

1614

24 а

251

1127

1659

3 а

27

903

1435

17 а

72

948

1480

2 а

117

993

1525

16 а

162

1038

1570

26 м

207

1083

1615

9 а

252

1128

1660

22 а

28

904

1436

8 а

73

949

1481

22 а

118

994

1526

1 а

163

1039

1571

15 а

208

1084

1616

31 м

253

1129

1661

14 а

29

905

1437

31 м

74

950

1482

7 а

119

995

1527

21 а

164

1040

1572

6 а

209

1085

1617

20 а

254

1130

1662

30 м

30

906

1438

13 а

75

951

1483

30 м

120

996

1528

12 а

165

1041

1573

22 м

210

1086

1618

5 а

255

1131

1663

19 а

31

907

1439

5 а

76

952

1484

18 а

121

997

1529

28 м

166

1042

1574

11 а

211

1087

1619

28 м

256

1132

1664

10 а

32

908

1440

27 м

77

953

1485

3 а

122

998

1530

17 а

167

1043

1575

3 а

212

1088

1620

16 а

257

1133

1665

26 м

33

909

1441

16 а

78

954

1486

26 м

123

999

1531

9 а

168

1044

1576

22 а

213

1089

1621

1 а

258

1134

1666

15 а

34

910

1442

1 а

79

955

1487

15 а

124

1000

1532

31 м

169

1045

1577

7 а

214

1090

1622

21 а

259

1135

1667

7 а

35

911

1443

21 а

80

956

1488

6 а

125

1001

1533

13 а

170

1046

1578

30 м

215

1091

1623

13 а

260

1136

1668

22 м

36

912

1444

12 а

81

957

1489

19 а

126

1002

1534

5 а

171

1047

1579

19 а

216

1092

1624

28 м

261

1137

1669

11 а

37

913

1445

28 м

82

958

1490

11 а

127

1003

1535

28 м

172

1048

1580

3 а

217

1093

1625

17 а

262

1138

1670

3 а

38

914

1446

17 а

83

959

1491

3 а

128

1004

1536

16 а

173

1049

1581

26 м

218

1094

1626

9 а

263

1139

1671

23 а

39

915

1447

9 а

84

960

1492

22 а

129

1005

1537

1 а

174

1050

1582

15 а

219

1095

1627

25 м

264

1140

1672

7 а

40

916

1448

24 м

85

961

1493

7 а

130

1006

1538

21 а

175

1051

1583

31 м

220

1096

1628

13 а

265

1141

1673

30 м

41

917

1449

13 а

86

962

1494

30 м

131

1007

1539

6 а

176

1052

1584

19 а

221

1097

1629

5 а

266

1142

1674

19 а

42

918

1450

5 а

87

963

1495

19 а

132

1008

1540

28 м

177

1053

1585

11 а

222

1098

1630

28 м

267

1143

1675

4 а

43

919

1451

25 а

88

964

1496

3 а

133

1009

1541

17 а

178

1054

1586

3 а

223

1099

1631

10 а

268

1144

1676

26 м

44

920

1452

9 а

89

965

1497

26 м

134

1010

1542

9 а

179

1055

1587

16 а

224

1100

1632

1 а

269

1145

1677

15 а

45

921

1453

1 а

90

966

1498

15 а

135

1011

1543

25 м

180

1056

1588

7 а

225

1101

1633

21 а

270

1146

1678

31 м

-58-59-

 Таблица XV

Обращение великого индиктиона (а=апрель, м=март) (Окончание)

NN
года
текущ.
инд-на

Индиктионы

Пасха

NN
года
текущ.
инд-на

Индиктионы

Пасха

NN
года
текущ.
инд-на

Индиктионы

Пасха

NN
года
текущ.

инд-на 

Индиктионы

Пасха

NN
года
текущ.

инд-на

Индиктионы

Пасха

NN
года
текущ.

инд-на

Индиктионы

Пасха

13

14

13

14

13

14

13

14

13

14

13

14

269

1145

1677

15 а

313

1189

1721

9 а

357

1233

1765

3 а

401

1277

1809

28 м

445

1321

1853

19 а

489

1365

1897

13 а

270

1146

1678

31 м

314

1190

1722

25 м

358

1234

1766

23 а

402

1278

1810

17 а

446

1322

1854

11 а

490

1366

1898

5 а

271

1147

1679

20 а

315

1191

1723

14 а

359

1235

1767

8 а

403

1279

1811

2 а

447

1323

1855

27 м

491

1367

1899

18 а

272

1148

1680

11 а

316

1192

1724

5 а

360

1236

1768

30 м

404

1280

1812

21 а

448

1324

1856

15 а

492

1368

1900

9 а

273

1149

1681

3 а

317

1193

1725

28 м

361

1237

1769

19 а

405

1281

1813

13 а

449

1325

1857

7 а

493

1369

1901

1 а

274

1150

1682

16 а

318

1194

1726

10 а

362

1238

1770

4 а

406

1282

1814

29 м

450

1326

1858

23 м

494

1370

1902

14 а

275

1151

1683

8 а

319

1195

1727

2 а

363

1239

1771

27 м

407

1283

1815

18 а

451

1327

1859

12 а

495

1371

1903

6 а

276

1152

1684

30 м

320

1196

1728

21 а

364

1240

1772

15 а

408

1284

1816

9 а

452

1328

1860

3 а

496

1372

1904

28 м

277

1153

1685

19 а

321

1197

1729

6 а

365

1241

1773

31 м

409

1285

1817

25 м

453

1329

1861

23 а

497

1373

1905

17 а

278

1154

1686

4 а

322

1198

1730

29 м

366

1242

1774

20 а

410

1286

1818

14 а

454

1330

1862

8 а

498

1374

1906

2 а

279

1155

1687

27 м

323

1199

1731

18 а

367

1243

1775

12 а

411

1287

1819

6 а

455

1331

1863

31 м

499

1375

1907

22 а

280

1156

1688

15 а

324

1200

1732

9 а

368

1244

1776

3 а

412

1288

1820

28 м

456

1332

1864

19 а

500

1376

1908

13 а

281

1157

1689

31 м

325

1201

1733

25 м

369

1245

1777

16 а

413

1289

1821

10 а

457

1333

1865

4 а

501

1377

1909

29 м

282

1158

1690

20 а

326

1202

1734

14 а

370

1246

1778

8 а

414

1290

1822

2 а

458

1334

1866

27 м

502

1378

1910

18 а

283

1159

1691

12 а

327

1203

1735

6 а

371

1247

1779

31 м

415

1291

1823

22 а

459

1335

1867

16 а

503

1379

1911

10 а

284

1160

1692

27 м

328

1204

1736

25 а

372

1248

1780

19 а

416

1292

1824

6 а

460

1336

1868

31 м

504

1380

1912

25 м

285

1161

1693

16 а

329

1205

1737

10 а

373

1249

1781

4 а

417

1293

1825

29 м

461

1337

1869

20 а

505

1381

1913

14 а

286

1162

1694

8 а

330

1206

1738

2 а

374

1250

1782

27 м

418

1294

1826

18 а

462

1338

1870

12 а

506

1382

1914

6 а

287

1163

1695

24 м

331

1207

1739

22 а

375

1251

1783

16 а

419

1295

1827

3 а

463

1339

1871

28 м

507

1383

1915

22 м

288

1164

1696

12 а

332

1208

1740

6 а

376

1252

1784

31 м

420

1296

1828

25 м

464

1340

1872

16 а

508

1384

1916

10 а

289

1165

1697

4 а

333

1209

1741

29 м

377

1253

1785

20 а

421

1297

1829

14 а

465

1341

1873

8 а

509

1385

1917

2 а

290

1166

1698

24 а

334

1210

1742

18 а

378

1254

1786

12 а

422

1298

1830

6 а

466

1342

1874

31 м

510

1386

1918

22 а

291

1167

1699

9 а

335

1211

1743

3 а

379

1255

1787

28 м

423

1299

1831

19 а

467

1343

1875

13 а

511

1387

1919

7 а

292

1168

1700

31 м

336

1212

1744

25 м

380

1256

1788

16 а

424

1300

1832

10 а

468

1344

1876

4 а

512

1388

1920

29 м

293

1169

1701

20 а

337

1213

1745

14 а

381

1257

1789

8 а

425

1301

1833

2 а

469

1345

1877

27 м

513

1389

1921

18 а

294

1170

1702

5 а

338

1214

1746

30 м

382

1258

1790

24 м

426

1302

1834

22 а

470

1346

1878

16 а

514

1390

1922

3 а

295

1171

1703

28 м

339

1215

1747

19 а

383

1259

1791

13 а

427

1303

1835

7 а

471

1347

1879

1 а

515

1391

1923

26 м

296

1172

1704

16 а

340

1216

1748

10 а

384

1260

1792

4 а

428

1304

1836

29 м

472

1348

1880

20 а

516

1392

1924

14 а

297

1173

1705

8 а

341

1217

1749

26 м

385

1261

1793

24 а

429

1305

1837

18 а

473

1349

1881

12 а

517

1393

1925

6 а

298

1174

1706

24 м

342

1218

1750

15 а

386

1262

1794

9 а

430

1306

1838

3 а

474

1350

1882

28 м

518

1394

1926

19 а

299

1175

1707

13 а

343

1219

1751

7 а

387

1263

1795

1 а

431

1307

1839

26 м

475

1351

1883

17 а

519

1395

1927

11 а

300

1176

1708

4 а

344

1220

1752

29 м

388

1264

1796

20 а

432

1308

1840

14 а

476

1352

1884

8 а

520

1396

1928

2 а

301

1177

1709

24 а

345

1221

1753

11 а

389

1265

1797

5 а

433

1309

1841

30 м

477

1353

1885

24 м

521

1397

1929

22 а

302

1178

1710

9 а

346

1222

1754

3 а

390

1266

1798

28 м

434

1310

1842

19 а

478

1354

1886

13 а

522

1398

1930

7 а

303

1179

1711

1 а

347

1223

1755

23 а

391

1267

1799

17 а

435

1311

1843

11 а

479

1355

1887

5 а

523

1399

1931

30 м

304

1180

1712

20 а

348

1224

1756

14 а

392

1268

1800

8 а

436

1312

1844

26 м

480

1356

1888

24 а

524

1400

1932

18 а

305

1181

1713

5 а

349

1225

1757

30 м

393

1269

1801

24 м

437

1313

1845

15 а

481

1357

1889

9 а

525

1401

1933

3 а

306

1182

1714

28 м

350

1226

1758

19 а

394

1270

1802

13 а

438

1314

1846

7 а

482

1358

1890

1 а

526

1402

1934

26 м

307

1183

1715

17 а

351

1227

1759

11 а

395

1271

1803

5 а

439

1315

1847

23 м

483

1359

1891

21 а

527

1403

1935

15 а

308

1184

1716

1 а

352

1228

1760

26 м

396

1272

1804

24 а

440

1316

1848

11 а

484

1360

1892

5 а

528

1404

1936

30 м

309

1185

1717

21 а

353

1229

1761

15 а

397

1273

1805

9 а

441

1317

1849

3 а

485

1361

1893

28 м

529

1405

1937

19 а

310

1186

1718

13 а

354

1230

1762

7 а

398

1274

1806

1 а

442

1318

1850

23 а

486

1362

1894

17 а

530

1406

1938

11 а

311

1187

1719

29 м

355

1231

1763

23 м

399

1275

1807

14 а

443

1319

1851

8 а

487

1363

1895

2 а

531

1407

1939

27 м

312

1188

1720

17 а

356

1232

1764

11 а

400

1276

1808

5 а

444

1320

1852

30 м

488

1364

1896

24 м

532

1408

1940

15 а

-60-61-

древне-русские документы. Мы остановимся естественно только на этом последнем варианте математических построений Гауса.
        Для вычисления пасхи по методу Гауса необходимо прежде всего найти значение нескольких математических величин, (которые можно обозначить буквами: a, b, c, d, e.
        Под a подразумевается остаток от деления цифрового обозначения года на 19. Под b имеется в виду остаток от деления того же цифрового, обозначения года на 4, а под c -- остаток от деления на 7; d = остатку от деления выражения (19a + 15) на 30. Для вычисления e берем остаток от деления выражения (2b + 4c + 6d + 6) на 7. В случае отсутствия остатка, a приравнивается делителю (т. е. 19), все остальные величины (b, c, d, e) -- нулю.
        В конечном итоге имеют значение только величины d и e. Все же остальные выражения (a, b, c) исполняют исключительно служебную роль, помогая определению d и e. Мы должны найти сумму d и e и посмотреть, превышает ли она число девять. Если дело обстоит именно так, то мы из этой суммы (d + e) вычитаем 9 и получаем дату апрельской пасхи. Если же окажется, что выражение (d + е) меньше 9 или равно ему, тогда необходимо к найденной сумме (d + е) прибавить 22 и в результате получится дата мартовской пасхи.
        Приведем примеры.
        Предположим, что нам нужно узнать, когда была пасха в 1424 г. Обозначим цифровой показатель года через букву N, а остаток от деления цифрового обозначения года на ряд последовательных чисел -- через букву R. Согласно формуле Гауса:
           a = R(N : 19) = R(1424 : 19) = 18.
           b = R(N : 4) = R(1424: 4) = 0.
           c = R(N : 7) = R(1424: 7) = 3.
           d = R[(19a + 15) : 30] = R[(19 × 18 + 15) : 30] = R[(342 + 15) : 30] = R(357 : 30) = 27.
           e = R[2b + 4c + 6d + 6) : 7] = R[(2 × 0 + 4 × 3 + 6 × 27 + 6) : 7] =
             = R[(4 × 3 + 6 × 27 + 6) : 7] = R[(12 + 162 + 6) : 7] = R(180 : 7) = 5.
           d + e = 27 + 5 = 32.
        32>9. Следовательно, дата 1424 г. = (32 - 9) апреля = 23 апреля.
        Другой пример: требуется вычислить день празднования пасхи в 1619 г.
           a = R(N : 19) = R(1619 : 19) = 4.
           b = R(N : 4) = R(1619 : 4) = 3.
           c = R(N : 7) = R(1619 : 7) = 2.
           d  = R[(19a + 15) : 30] = R[(19 × 4 + 15) : 30] = R[(76 + 15) : 30] =
             = R(91 : 30) = 1.
           e = R[2b + 4c + 6d + 6) : 7] = R[(2 × 3 + 4 × 2 + 6 × 1 + 6) : 7] =
             R[(6 + 8 + 6 + 6) : 7] = R(26 : 7) = 5.
           d + e = 1 + 5 = 6.

-62-

        69. Следовательно, дата пасхи 1619 г. = (6 + 22) марта = 28 марта.
        В заключение отметим, что пользоваться формулой Гауса можно только для дат нашей эры. Поэтому, если в источниках нам встретится дата по византийскому летосчислению, то ее прежде всего надо перевести на современную эру, а затем уже применять к ней формулу Гауса.
         § 23. Датировка подвижными праздниками. Исходя из дня празднования пасхи в том или ином году, уже не трудно определить любую подвижную церковную дату для этого года, т. к. переходящие праздники и посты всегда отстоят от пасхи на строго определенное количество дней. Все эти подвижные церковные даты можно разбить на две категории: они или предшествуют пасхе, или же следуют за ней.
        Начнем наш обзор с первой категории. Останавливаясь лишь на основных церковных подвижных датах, откроем церковный календарь девятой неделей до пасхи, называемой мясопустной или пестрой. Она заканчивается мясопустным воскресеньем (за 56 суток до пасхи). Затем следует сырная неделя или масленица. Воскресенье на сырной неделе, предшествующее пасхе ма 49 суток, носит название сыропустного или заговенья. Вслед за ним наступает великий пост ("говенье", "гавейно"). Он продолжается семь недель. Первая неделя именуется Федоровой, а завершающее эту неделю (воскресенье -- соборным ("сборным", "зборным", -- за 42 суток до пасхи). Затем последовательно идут следующие недели поста: вторая (считая от начала поста), третья (безъимянная, с крестопоклонным или средокрестным воскресеньем, -- за 28 суток до пасхи), четвертая (крестопоклонная), пятая (похвальная), шестая (вербная) и седьмая (страстная, непосредственно предшествующая пасхальному воскресенью).
        В пасхальном церковном календаре счет недель до пасхи ведется с понедельника по воскресенье включительно. Но после пасхи этот счет изменяется: недели открываются воскрeceньем и заканчиваются субботой. Так воскресенье, непосредственно идущее за пасхальным (через 7 суток), именуется Фоминым и с него начинается Фомина неделя (вторая после пасхи). Из подвижных праздников, имеющих место в после-пасхальный период, достаточно отметить следующие: преполовение -- на 25-е сутки после пасхи, вознесение -- на 40-е сутки, троица или пятидесятница -- на 50-е сутки, духов день -- на 51-е сутки и т. д.
        Узнав число празднования пасхи и прибавив к нему, или наоборот, отняв от него, количество дней, отделяющих пасхальное воскресение от подвижной даты (пасхального календаря, упоминаемой в источнике, мы легко установим эту дату. Например, если пасха празднуется 23 апреля, то вербное воскресенье (за 7 суток) -- естественно придется 16 апреля, мясопуст (за 56 суток) -- 26 февраля (в простом году) и 27 февраля (в високосном), преполовение (на 25-е сутки) -- 17 мая, вознесение (на 40-е сутки) -- 1 июня и т. д.

-63-

        Несколько сложнее обстоит дело в том случае, если документ датирован посредством ссылки на день среди недели; например: "в пятницу на Федоровой неделе". Тогда приходится рассуждать так: Федорова неделя это -- первая неделя великого поста (из семи). Следовательно, заканчивающее эту неделю воскресенье (сборное) бывает за 42 суток до пасхального воскресенья, а пятница -- за 44 суток. Если пасха -- 23 апреля, то пятница на Федоровой неделе -- 10 марта.
        Для облегчения вычислений ниже помещается таблица XVI. В ней указаны числа, на которые падают подвижные церковные календарные даты, в зависимости от того, когда в данном году празднуется паска. Определив предварительно день пасхи для интересующего нас года, мы находим соответствующие месяц и число в левой крайней графе, а рядом с ним помещены числа для любого подвижного праздника, связанного с пасхой.
         § 24. Ключевые буквы. Зрячая пасхалия. Выше было указано, что "пасхальным пределом" является период времени с 22 марта по 25 апреля включительно, составляющий в общей сложности 35 суток. Пасха может праздноваться в один из дней только в этих границах. Порядковое место пасхи данного года в пасхальном пределе называется ключем границ. Например, в 1573 г. пасха приходится на 22 марта (ом. таблицу XV). Это -- наиболее ранний (первый из числа возможных) день пасхи. Следовательно, ключ границ 1573 г. = 1. В 1600 г. пасхальное воскресенье совпало с 23 марта (вторым по счету днем в 35-дневном пасхальном пределе). (см. ту же таблицу). Отсюда заключаем, что ключем границ для 1600 г. будет число 2. Рассуждая таким же образом далее, найдем, что самый большой ключ границ (35) будет иметь тот год, в котором пасха празднуется в наиболее поздний (крайний) срок.
        Технически определение ключа границ очень не сложно. Для мартовской пасхи оно производится путем вычитания из даты пасхального воскресенья числа 21, для апрельской -- путем прибавления к пасхальной дате числа 10. Например, в N-ом году пасха была 27 марта. Ключ границ этого года = 27 - 21 = 6. В N1-м году пасха -- 7 апреля. Следовательно, ключ границ = 7 + 10 = 17.
        В древне-русских пасхальных календарях ключевые цифры (1 -- 35) заменялись ключевыми буквами; причем для этой цели брались не только те из них, которые имели постоянное цифровое значение, но и такие буквы как б или ж, которые вообще говоря, в значении цифр не употреблялись. Просто соблюдалась обычная последовательность славянского алфавита, без всяких пропусков. Ключевая буква приобретала чисто условное значение. Каждому году соответствовала одна из 35 ключевых букв, которая определяла в данном году все даты подвижного пасхального календаря, начиная с основной -- пасхи.
        В древней Руси существовала особая таблица, известная под названием зрячей пасхалии. Она состояла из 35 ключевых букв, против которых указывались соответствующие подвижные церковные даты. Кроме того, зрячая пасхалия включала и даты неподвижных

 Таблица XVI

Календарь подвижных церковных дат (до пасхи)

Пасха

Неделя мясопустная
(пестрая)

Неделя сырная (масляница)

1-я неделя великого
поста (Федорова)

2-я неделя великого
поста

3-я неделя великого
поста (безымянная)

4-я неделя великого поста
(крестопоклонная)

5-я неделя великого поста
(похвальная)

6-я неделя великого поста
(вербная)

7-я неделя великого поста
(страстная)

 

Мясопуст

 

Заговенье,
Сыропуст

 

Соборное
воскресенье

 

 

 

Крестопокл.
Средокрест.
воскрес.

прост

висок

прост

висок

прост

висок

прост

висок

прост

висок

прост

висок

прост

висок

прост

висок

прост

висок

прост

висок

прост

висок

всяк

понедельник

воскресенье

понедельник

воскресенье

понедельник

воскресенье

понедельник

воскресенье

понедельник

воскресенье

понедельник

воскр

понед

воскр

понед

воскр

понед

субб

22мар

19янв

20янв

25янв

26янв

26янв

27янв

1февр

2февр

2февр

3февр

8февр

9февр

9февр

10февр

15февр

16февр

16февр

17февр

22февр

23февр

23февр

24февр

1мар

2мар

8мар

9мар

15мар

16мар

21мар

23

20

21

26

27

27

28

2

3

3

4

9

10

10

11

16

17

17

18

23

24

24

25

2

3

9

10

16

17

22

24

21

22

27

28

28

29

3

4

4

5

10

11

11

12

17

18

18

19

24

25

25

26

3

4

10

11

17

18

23

25

22

23

28

29

29

30

4

5

5

6

11

12

12

13

18

19

19

20

25

26

26

27

4

5

11

12

18

19

24

26

23

24

29

30

30

31

5

6

6

7

12

13

13

14

19

20

20

21

26

27

27

28

5

6

12

13

19

20

25

27

24

25

30

31

31

1февр

6

7

7

8

13

14

14

15

20

21

21

22

27

28

28

29

6

7

13

14

20

21

26

28

25

26

31

1февр

1февр

2

7

8

8

9

14

15

15

16

21

22

22

23

28

29

1мар

1мар

7

8

14

15

21

22

27

29

26

27

1февр

2

2

3

8

9

9

10

15

16

16

17

22

23

23

24

1мар

1мар

2

2

8

9

15

16

22

23

28

30

27

28

2

3

3

4

9

10

10

11

16

17

17

18

23

24

24

25

2

2

3

3

9

10

16

17

23

24

29

31

28

29

3

4

4

5

10

11

11

12

17

18

18

19

24

25

25

26

3

3

4

4

10

11

17

18

24

25

30

1апр

29

30

4

5

5

6

11

12

12

13

18

19

19

20

25

26

26

27

4

4

5

5

11

12

18

19

25

26

31

2

30

31

5

6

6

7

12

13

13

14

19

20

20

21

26

27

27

28

5

5

6

6

12

13

19

20

26

27

1апр

3

31

1февр

6

7

7

8

13

14

14

15

20

21

21

22

27

28

28

29

6

6

7

7

13

14

20

21

27

28

2

4

1февр

2

7

8

8

9

14

15

15

16

21

22

22

23

28

29

1мар

1мар

7

7

8

8

14

15

21

22

28

29

3

5

2

3

8

9

9

10

15

16

16

17

22

23

23

24

1мар

1мар

2

2

8

8

9

9

15

16

22

23

29

30

4

6

3

4

9

10

10

11

16

17

17

18

23

24

24

25

2

2

3

3

9

9

10

10

16

17

23

24

30

31

5

7

4

5

10

11

11

12

17

18

18

19

24

25

25

26

3

3

4

4

10

10

11

11

17

18

24

25

31

1апр

6

8

5

6

11

12

12

13

18

19

19

20

25

26

26

27

4

4

5

5

11

11

12

12

18

19

25

26

1апр

2

7

9

6

7

12

13

13

14

19

20

20

21

26

27

27

28

5

5

6

6

12

12

13

13

19

20

26

27

2

3

8

10

7

8

13

14

14

15

20

21

21

22

27

28

28

29

6

6

7

7

13

13

14

14

20

21

27

28

3

4

9

11

8

9

14

15

15

16

21

22

22

23

28

29

1мар

1мар

7

7

8

8

14

14

15

15

21

22

28

29

4

5

10

12

9

10

15

16

16

17

22

23

23

24

1мар

1мар

2

2

8

8

9

9

15

15

16

16

22

23

29

30

5

6

11

13

10

11

16

17

17

18

23

24

24

25

2

2

3

3

9

9

10

10

16

16

17

17

23

24

30

31

6

7

12

14

11

12

17

18

18

19

24

25

25

26

3

3

4

4

10

10

11

11

17

17

18

18

24

25

31

1апр

7

8

13

15

12

13

18

19

19

20

25

26

26

27

4

4

5

5

11

11

12

12

18

18

19

19

25

26

1апр

2

8

9

14

16

13

14

19

20

20

21

26

27

27

28

5

5

6

6

12

12

13

13

19

19

20

20

26

27

2

3

9

10

15

17

14

15

20

21

21

22

27

28

28

29

6

6

7

7

13

13

14

14

20

20

21

21

27

28

3

4

10

11

16

18

15

16

21

22

22

23

28

29

1мар

1мар

7

7

8

8

14

14

15

15

21

21

22

22

28

29

4

5

11

12

17

19

16

17

22

23

23

24

1мар

1мар

2

2

8

8

9

9

15

15

16

16

22

22

23

23

29

30

5

6

12

13

18

20

17

18

23

24

24

25

2

2

3

3

9

9

10

10

16

16

17

17

23

23

24

24

30

31

6

7

13

14

19

21

18

19

24

25

25

26

3

3

4

4

10

10

11

11

17

17

18

18

24

24

25

25

31

1апр

7

8

14

15

20

22

19

20

25

26

26

27

4

4

5

5

11

11

12

12

18

18

19

19

25

25

26

26

1апр

2

8

9

15

16

21

23

20

21

26

27

27

28

5

5

6

6

12

12

13

13

19

19

20

20

26

26

27

27

2

3

9

10

16

17

22

24

21

22

27

28

28

29

6

6

7

7

13

13

14

14

20

20

21

21

27

27

28

28

3

4

10

11

17

18

23

25

22

23

28

29

1мар

1мар

7

7

8

8

14

14

15

15

21

21

22

22

28

28

29

29

4

5

11

12

18

19

24

 Таблица XVI

Календарь подвижных церковных дат (после пасхи)

1 неделя по
пасхе

2 неделя по
пасхе (фомина)

3 неделя по
пасхе

4 неделя по
пасхе

5 неделя по
пасхе

6 неделя по
пасхе

7 неделя по
пасхе

8 неделя по
пасхе

Пасха

 

Фомина
воскр.

Радуница

 

 

 

Препо-
ловение

 

 

 

Вознесение

 

Семик

Пятиде-
сятница
(троица)

Духов
день

Воскр.

Субб.

Воскр.

Втор.

Воскр.

Субб.

Воскр.

Среда

Воскр.

Субб.

Воскр.

Четв.

Воскр.

Четв.

Воскр.

Понед.

22 мар

28 мар

29 мар

31 мар

5 апр

11 апр

12 апр

15 апр

19 апр

25 апр

26 апр

30 апр

3 мая

7 мая

10 мая

11 мая

23

29

30

1 апр

6

12

13

16

20

26

27

1 мая

4

8

11

12

24

30

31

2

7

13

14

17

21

27

28

2

5

9

12

13

25

31

1 апр

3

8

14

15

18

22

28

29

3

6

10

13

14

26

1 апр

2

4

9

15

16

19

23

29

30

4

7

11

14

15

27

2

3

5

10

16

17

20

24

30

1 мая

5

8

12

15

16

28

3

4

6

11

17

18

21

25

1 мая

2

6

9

13

16

17

29

4

5

7

12

18

19

22

26

2

3

7

10

14

17

18

30

5

6

8

13

19

20

23

27

3

4

8

11

15

18

19

31

6

7

9

14

20

21

24

28

4

5

9

12

16

19

20

1 апр

7

8

10

15

21

22

25

29

5

6

10

13

17

20

21

2

8

9

11

16

22

23

26

30

6

7

11

14

18

21

22

3

9

10

12

17

23

24

27

1 мая

7

8

12

15

19

22

23

4

10

11

13

18

24

25

28

2

8

9

13

16

20

23

24

5

11

12

14

19

25

26

29

3

9

10

14

17

21

24

25

6

12

13

15

20

26

27

30

4

10

11

15

18

22

25

26

7

13

14

16

21

27

28

1 мая

5

11

12

16

19

23

26

27

8

14

15

17

22

28

29

2

6

12

13

17

20

24

27

28

9

15

16

18

23

29

30

3

7

13

14

18

21

25

28

29

10

16

17

19

24

30

1 мая

4

8

14

15

19

22

26

29

30

11

17

18

20

25

1 мая

2

5

9

15

16

20

23

27

30

31

12

18

19

21

26

2

3

6

10

16

17

21

24

28

31

1 июня

13

19

20

22

27

3

4

7

11

17

18

22

25

29

1 июня

2

14

20

21

23

28

4

5

8

12

18

19

23

26

30

2

3

15

21

22

24

29

5

6

9

13

19

20

24

27

31

3

4

16

22

23

25

30

6

7

10

14

20

21

25

28

1 июня

4

5

17

23

24

26

1 мая

7

8

11

15

21

22

26

29

2

5

6

18

24

25

27

2

8

9

12

16

22

23

27

30

3

6

7

19

25

26

28

3

9

10

13

17

23

24

28

31

4

7

8

20

26

27

29

4

10

11

14

18

24

25

29

1 июня

5

8

9

21

27

28

30

5

11

12

15

19

25

26

30

2

6

9

10

22

28

29

1 мая

6

12

13

16

20

26

27

31

3

7

10

11

23

29

30

2

7

13

14

17

21

27

28

1 июня

4

8

11

12

24

30

1 мая

3

8

14

15

18

22

28

29

2

5

9

12

13

25

1 мая

2

4

9

15

16

19

23

29

30

3

6

10

13

14

-64-

праздников (например, рождество или благовещение) и приводила их в связь с определенными моментами подвижного церковного календаря. Скажем, благовещение всегда празднуется 25 марта, но в зависимости от дня пасхи оно в различные годы может совпасть или с пасхальной неделей или же с тем или иным моментом великого поста. Таким образом, зрячая пасхалия представляла собой интересную попытку сочетать данные постоянного солнечного Юлианского календаря с данными календаря передвижного, пасхального, лунного по своему построению, церковного по назначению.
         § 25. Датировка по астрономическим явлениям. В русских источниках, особенно в летописных сводах, часто встречаются указания на солнечные и лунные затмения, кометы, падающие звезды, солнечные пятна и т. д. В астрономических явлениях наблюдается строгая закономерность. Поэтому, будучи подвергнуты соответственной научно-критической обработке, эти известия дают в руки исследователей -материал для установления или уточнения хронологических данных.
         § 26. Солнечные и лунные затмения. Специалистами в области астрономии (составлены особые таблицы, которые дают возможность выяснить, может ли (или даже должно ли обязательно) произойти затмение солнца или луны в данный день того или иного месяца и года. Для разрешения этого вопроса прежде всего интересующие нас месяц и число превращаются в десятичную дробь года. Это, делается при помощи помещаемой ниже таблицы XVII, в четных столбцах которой ищется нужная дата, а в нечетных -- соответствующая ей дробь года.

 Таблица XVII

Перевод месяца и числа в десятичную дробь года

0.00

Январь

1-2

0.25

Апрель

1-4

0.50

Июль

1-4

0.75

Окт.

1-3

0.01

    "

3-6

0.26

    "

5-7

0.51

    "

5-8

0.76

    "

4-7

0.02

    "

7-10

0.27

    "

8-11

0.52

    "

9-11

0.77

    "

8-11

0.03

    "

11-13

0.28

    "

12-15

0.53

    "

12-15

0.78

    "

12-14

0.04

    "

14-17

0.29

    "

16-18

0.54

    "

16-19

0.79

    "

15-18

0.05

    "

18-21

0.30

    "

19-22

0.55

    "

20-22

0.80

    "

19-22

0.06

    "

22-24

0.31

    "

23-26

0.56

    "

23-26

0.81

    "

23-25

0.07

    "

25-28

0.32

    "

27-29

0.57

    "

27-30

0.82

    "

26-29

0.08

Февраль

29-1

0.33

Май

30-3

0.58

Август

31-2

0.83

Ноябрь

30-1

0.09

    "

2-4

0.34

    "

4-7

0.59

    "

3-6

0.84

    "

2-5

0.10

    "

5-8

0.35

    "

8-10

0.60

    "

7-9

0.85

    "

6-9

0.11

    "

9-11

0.36

    "

11-14

0.61

    "

10-13

0.86

    "

10-12

0.12

    "

12-15

0.37

    "

15-17

0.62

    "

14-17

0.87

    "

13-16

0.13

    "

16-19

0.38

    "

18-21

0.63

    "

18-20

0.88

    "

17-20

0.14

    "

20-22

0.39

    "

22-25

0.64

    "

21-24

0.89

    "

21-23

0.15

    "

23-26

0.40

    "

26-28

0.65

    "

25-28

0.90

    "

24-27

0.16

Март

27-2

0.41

Июнь

29-1

0.66

    "

29-31

0.91

Декабрь

28-1

0.17

    "

3-5

0.42

    "

2-5

0.67

Сентябрь

1-4

0.92

    "

2-4

0.18

    "

6-9

0.43

    "

6-8

0.68

    "

5-8

0.93

    "

5-8

0.19

    "

10-13

0.44

    "

9-12

0.69

    "

9-11

0.94

    "

9-12

0.20

    "

14-16

0.45

    "

13-16

0.70

    "

12-15

0.95

    "

13-15

0.21

    "

17-20

0.46

    "

17-19

0.71

    "

16-19

0.96

    "

16-19

0.22

    "

21-24

0.47

    "

20-23

0.72

    "

20-22

0.97

    "

20-23

0.23

    "

25-27

0.48

    "

24-27

0.73

    "

23-26

0.98

    "

24-26

0.24

    "

28-31

0.49

    "

28-30

0.74

    "

27-30

0.99

    "

27-31

-65-

        К найденной дроби прибавляется год рассматриваемой даты, Например, мы хотим узнать, могло ли быть 7 июня 1415 г. солнечное затмение. Против 7 июня в таблице находится дробь 0,43; 1415 +0,43 =1415,43.
        Обращаемся к следующей таблице XVIII, в которой выбираем ближайшее к нашей дате (выраженной в виде целого с дробью), но обязательно меньшее число.

 Таблица XVIII

Солнечные и лунные затмения

1.44

280.45

587.92

895.40

1202.87

1510.35

1817.82

1.92

309.40

616.87

924.34

1231.82

1539.29

1846.77

30.87

338.34

645.81

953.29

1260.76

1568.24

1875.71

59.81

367.28

674.76

982.23

1289.71

1597.19

1904.66

88.75

396.23

703.70

1000.26

1307.74

1615.22

1933.60

117.70

425.17

732.65

1029.21

1336.68

1644.16

1951.63

146.64

454.12

750.68

1058.15

1365.62

1673.11

1980.58

175.59

472.15

779.62

1087.10

1394.57

1702.05

2009.52

204.53

501.09

808.57

1116.04

1423.51

1731.00

2038.47

233.48

530.04

837.51

1144.98

1452.46

1759.94

2067.41

251.51

558.98

866.45

1173.93

1481.40

1788.89

2096.36


        Ближайшим (меньшим) числом к дате 1415,43 будет 1394,57. Мы должны его вычесть из разбираемой даты. 1415,43 - 1394,57 = =20,86.
        Полученную разность мы и отыскиваем в последней, ниже помещаемой таблице XIX. Наличие там числа, равного этой разности, или отличающегося от него на 1--2 сотых, свидетельствует о возможности для нашей даты затмения: солнечного (при знаке "с") и лунного (при букве "л"). А если, кроме того, нам встретится знак восклицания (!), то это указывает на то, что затмение (солнечное или лунное) не только возможно, но должно произойти обязательно. Буква "п" означает полное лунное или центральное солнечное затмение, буква "ч" -- частное. Отсутствие в таблице искомого числа (или близкого к нему в указанных пределах) говорит о том, что рассматриваемая нами дата для затмения абсолютно невероятна.
        Полученная нами разность 20,86 находится в таблице под восклицательным знаком и в сопровождении букв с. п. Это значит, что 7 июня 1415 г. без сомнения было полное солнечное затмение.
        В целях уточнения хронологических расчетов существуют еще таблицы определения степени видимости частных затмений для тех или иных точек земного шара, но на этом детально останавливаться нет надобности.
        На некоторых конкретных примерах продемонстрируем значение астрономических данных для русской хронологии. В летописи помещена заметка о солнечном затмении 4 сентября 6695 г. Для перевода даты на нашу эру нам нужно знать, каким календарным стилем пользуется летописец, т. к. в случае мартовской системы, для события, случившегося в сентябре, придется вычесть из даты число 5508, в случае сентябрьской -- 5509. Определить стиль помогает ссылала на солнечное затмение. В самом деле возьмем оба

-66-

возможных при переводе (в зависимости, от стиля) года по эре от "рождества христова" -- 1186 и 1187 (6695 - 5509=1186; 6695 - 5608 = 1187) и посмотрим, для какого из них можно допустить на 4 сентября затмение солнца. 4 сентября, выраженное дробью, по таблице XVII -- 0,67; 1186 + 0,67 = 1186,67; 1187 + 0,67 = 1187,67. Ближайшее число, к 1186,67 или к 1187,67 (по таблице XVIII) -- 1173,93; 1186,67 - 1173,93 = 12,74; 1187,67 -1173,93 = 13,74. Числа 12,74 в таблице XIX не находим, а 13,74 там имеется с восклицательным знаком и буквами с. п. Следовательно, 4 сентября 1187 обязательно имело место полное затмение солнца. Таким образом, приходим к выводу, что дата 6695 г. приведена по мартовскому стилю и соответствует 1187 г. (а никак не 1186 г.) нашей эры.

 Таблица XIX

Солнечные и лунные затмения

0.00 с. п.!

5.70 л. ч.!

11.84 л. ч.!

17.10 л. ч.!

23.24 л. ч.!

0.04 л. ч.

5.74 с. ч.

11.88 с. ч.

17.54 с. п.!

23.28 с. ч.!

0.44 л. ч.

6.14 с. ч.!

12.29 с. ч.

17.58 л. ч.

23.69 с. ч.!

0.49 с. п.!

6.19 л. ч.!

12.33 л. ч.!

18.03 с. п.!

23.73 л. ч.!

0.93 л. ч.

6.63 с. п.!

12.37 с. ч.!

18.07 л. ч.

23.77 с. ч.

0.97 с. ч.!

6.67 л. ч.

12.77 с. ч.

18.47 л. ч.

24.17 с. ч.!

1.37 с. ч.

7.11 с. п.!

12.81 л. п.!

18.51 с. п.!

24.21 л. ч.!

1.41 л. ч.!

7.16 л. ч.

12.86 с. ч.

18.96 л. ч.

24.66 с. п.!

1.46 с. ч.!

7.56 л. ч.

13.26 с. ч.!

19.00 с. ч.!

24.70 л. ч.

1.86 с. ч.

7.60 с. п.!

13.30 л. ч.!

19.40 с. ч.

25.14 с. п.!

1.90 л. п.!

8.04 л. ч.

13.34 с. ч.

19.44 л. ч.!

25.18 л. ч.

1.94 с. ч.

8.09 с. п.!

13.74 с. п.!

19.48 с. ч.!

25.59 л. ч.

2.34 с. ч.!

8.49 с. ч.

13.78 л. ч.

19.89 с. ч.

25.63 с. п.!

2.39 л. ч.!

8.53 л. ч.!

14.23 с. п.!

19.93 л. п.!

26.07 л. ч.

2.43 с. ч.

8.57 с. ч.!

14.27 л. ч.

19.97 с. ч.

26.11 с. п.!

2.83 с. п.!

8.97 с. ч.

14.67 л. ч.

20.37 с. ч.!

26.52 с. ч.

2.87 л. ч.

9.01 л. п.!

14.71 с. п.!

20.41 л. ч.!

26.56 л. ч.!

3.31 с. п.!

9.06 с. ч.

15.16 л. ч.

20.46 с. ч.

26.60 с. ч.!

3.36 л. ч.

9.46 с. ч.!

15.20 с. п.!

20.86 с. п.!

27.00 с. ч.

3.76 л. ч.

9.50 л. ч.!

15.60 с. ч.

20.90 л. ч.

27.04 л. п.!

3.80 с. п.!

9.54 с. ч.

15.64 л. ч.!

21.34 с. п.!

27.08 с. ч.

4.24 л. ч.

9.94 с. п.!

15.68 с. ч.!

21.38 л. ч.

27.49 с. ч.!

4.29 с. п.!

9.98 л. ч.

16.09 с. ч.

21.79 л. ч.

27.53 л. ч.!

4.73 л. ч.!

10.43 с. п.!

16.13 л. п.!

21.83 с. ч.

27.57 с. ч.

4.77 с. ч.!

10.47 л. ч.

16.17 с. ч.

22.27 л. п.!

27.97 с. ч.!

5.17 с. ч.

10.87 л. ч.

16.57 с. ч.!

22.31 с. п.!

28.01 л. ч.

5.21 л. ч.!

10.91 с. п.!

16.61 л. ч.!

22.76 л. ч.!

28.46 с. п.!

5.26 с. ч.!

11.36 л. ч.

16.66 с. ч.

22.80 с. ч.!

28.50 л. ч.

5.66 с. ч.!

11.40 с. п.!

17.06 с. ч.!

23.20 с. ч.

28.90 л. ч.


        Другой пример: источник говорит о лунном затмении 3 февраля 6715 г.
        3 февраля 6715 г. падает или на 1208 г. нашей эры (в случае мартовского стиля: 6715 - 5507 = 1208) или 1207 г. (при сентябрьском стиле: 6715 - 5508 = 1207). Дробное выражение 3 февраля по таблице XVII - 0,09; 1208 + 0,09 = 1208,09; 1207 + 0,09 = = 1207,09. Ближайшее в таблице XVIII к указанным цифрам число -- 1202,87; 1208,09 - 1202,87 = 5,22; 1207,09 - 1202,87=4,22.

-67-

В таблице XIX находим число 5,21 с восклицательным знаком и буквами л. ч. Затмение луны было 3 февраля 1208 года, которому и отвечает 6715 (календарный мартовский) год византийской эры.
         § 27. Кометы. Для проверки и уточнения дат большое значение имеют, наряду с описаниями солнечных и лунных затмений, также указания на кометы, встречающиеся в ряде древне-русских источников летописного типа. Так например, в летописных сводах неоднократно отмечается периодическая комета Галлея, возвращающаяся в среднем через 76 лет. Ученые вычислили не только годы всех появлений кометы Галлея в прошлом, но и даты ее прохождения через перигелий 1) при каждом появлении. Эти данные сведены в помещаемую ниже таблицу XX, обнимающую период с X по XVII в. включительно. В нее включены сведения о главных отмеченных летописями кометах, причем комета Галлея выделена курсивом.

 Таблица XX

Кометы

Годы появления комет

Даты прохождения комет через перигелий

912

19 июля

989

15 сентября

1066

27 марта

1106

---

1145

29 апреля

1222

15 сентября

1264

19 июля

1301

22 октября

1366

13 октября

1378

8 ноября

1402

---

1456

8 июня

1472

18 февраля

1490

26 августа

1531

24 декабря

1532

19 октября

1533

14 июня

1556

22 апреля

1580

28 ноября

1607

27 октября

1664

4 декабря

1680

17 декабря

1682

15 сентября


        Покажем на конкретном примере, какую большую помощь оказывает эта таблица занимающимся вопросами русской хронологии:
        Под 6810 г в летописи имеется описание кометы в следующих образных выражениях: "того же лета бысть знамение на небеси: явися звезда на запади, луча вверх изпущая яко хвост, к полуднию ниць". Если бы мы не знали, на основании астрономических расчетов, в какие годы наблюдались появления комет, мы не смогли бы дать точного перевода приведенной летописной даты, на нашу эру. В самом деле, нам не указан ни календарный стиль, ми месяц,
        ___________
        1) Перигелием называется точка орбиты кометы, ближайшая к солнцу.

-68-

на который падало описываемое событие. Мы находимся в затруднении, какое же число вычитать из даты византийского летосчисления. 6810 г. от "сотворения мира" может соответствовать по современному летосчислению и 1303г. (6810 - 5507), и 1302г. (6810 -5508) и 1301 г. (6810 - 5509). И только справившись в приведенной выше таблице, мы убеждаемся, что речь идет именно о 1301 г., т. к. 22 октября этого года комета Галлея проходила через перигелий.
        В вопросах датировки приходится также руководствоваться и имеющимися в источниках данными о метеорах, падающих звездах, солнечных пятнах и т. д. Подробно на этом останавливаться мы не будем.

 III. ПРОВЕРКА ВСТРЕЧАЮЩИХСЯ В ИСТОЧНИКАХ ДАТ

         § 1. Ошибочные даты в древне-русских актах. Задача перевода дат с византийского летосчисления на современное сильно осложняется тем, что в древне-русских документах мы часто находим неверные цифровые обозначения годов. Мы оставим пока в стороне вопрос о применении заведомо неправильных принципов датировки древними летописцами. Этого вопроса мы коснемся ниже. А пока остановимся на хронологии актового материала и отметим возможные и часто встречающиеся на практике искажения действительных дат, в результате случайных причин, при механической или не достаточно точной переписке. Цифры пропускались, заменялись одна другой, тринимались одна за другую и т. д. От времени документы портились, поэтому в некоторых датах стирались отдельные цифры. Позднейшие копиисты не обращали на это внимания и воспроизводили цифровое указание источника в неполном виде, искажая тем самым его смысл.
        Можно указать несколько типичных случаев таких искажений.
        Часто отдельные цифры в дате оказываются переставленными. Например: "в лето ‡SМЦИ-ое", вместо "‡ SЦМИ-ое" (6948-е).
        Иногда из даты выпадают десятки или сотни лет. Так вместо "лета шесть тысяч девятьсот семьдесят четвертого" встречаем: "лета шесть тысяч девятьсот четвертого". Или в источнике стоит "РS" (106-й, т .е. 7106-й) год, в то время, как по смыслу следует ожидать "РКS" (126-й, т. е. 7126-й). Дату "‡SНЗ" (6057) следует пополнить числом "Ц" (900) = "‡ SЦНЗ" (6957) и т. д.
        Наблюдаются случаи ошибок на целое столетие. В грамоте XV в. можно натолкнуться на дату 7099 ("‡ЗЧ"), в то время, как должно быть: 7999 ("‡ ЗЦЧ").
        Часто употребляются, одна вместо другой, похожие по своему обозначению цифры, например: 80 (П), 50(Н) и 8 (И).
        Наконец, иногда буква "Е" в конце порядковых числительных принимается за цифру и читается как 5. Скажем: "‡ SЦМ-е (6940-е) лето" можно прочесть как 6945 ("‡ SЦМЕ"). И наоборот, буквенный значок для чиста 5 (Е), утеряв титло, выступает в своем первоначальном значении буквы. Дата "‡ SЦМЕ" (6945) понимается в таком случае за "‡ SЦМ-е" (6940-е).

-69-

        Иногда неверная дата является следствием и намеренной фальсификации.
         § 2. Проверка дат древне-русских актов. Учитывая возможность ошибок в хронологических данных исторических источников, историк обязан произвести проверку тех дат, которые он встречает в документах. Установить неточность в датировке и найти ключ к исправлению последней часто помогают, как мы уже видели, некоторые дополнительные признаки, сопровождающие в источнике дату, -- индикты, указания на дни недели, подвижные праздники и т. п. Но, во-первых, эти дополнительные данные не всегда в источниках имеются, во-вторых, их расхождение с основной датой не всегда поддается объяснению. В таком случае в целях исторической проверки дат приходится привлекать косвенные признаки.
        Проверка эта заключается в том, что из источника извлекаются все указания на исторических лиц, на учреждения, события и т. д. Затем подбирается из различных смежных источников хронологический материал, относящийся к этим лицам, учреждениям, событиям. Поскольку удается установить соответствие привлеченного дополнительно косвенного материала имеющейся в документе прямой дате, постольку отпадает вопрос об ее неверности. В случае же противоречия подобранных косвенных хронологических данных дате документа, последняя берется под сомнение, и, по возможности, исправляется.
        В числе тех косвенных признаков, которыми оперирует исследователь, осуществляя задачу исторической проверки дат, встречающихся в актах, видное место принадлежит титулам представителей верховной власти. Форма титула подвергалась видоизменениям, которые вызывались переменами в политическом укладе Русского государства. В Киевский период и в эпоху феодальной раздробленности, с ее системой великих и удельных княжений, употреблялся княжеский титул (форма: "князь" или "великий князь", а с 80-х годов XV. в. -- "великий князь всеа Руси"), После венчания в 1547 г. Ивана IV на царство, княжеский титул был заменен царским (форма: "царь и великий князь всеа Русии", "государь царь и великий князь всеа Русии" затем -- "всеа Русии самодержец"). Присоединение в 1654 г. Украины и Смоленской области внесло некоторые дальнейшие изменения в форму царского титула. Вместо "государь царь и великий князь всеа Русии самодержец", стали писать: "государь царь и великий князь всеа Великия и Малыя и Белыя Русии самодержец". Такой вариант царского титула подчеркивал расширение пределов Московского государства.
        Соответственные изменения претерпел и титул представителей высшей русской церковной иерархии. До 1589 г. во главе русской церкви стоял московский митрополит. После учреждения в 1589 г. патриаршества, московский митрополит получает титул патриарха.
        В документе может встретиться явное несоответствие даты и титула того представителя верховной власти, светской или церковной, от лица которого издан документ. Так в одной жалованной грамоте, данной от имени "великого князя Ивана Васильевича всеа

-70-

России", стоит 7056 год. В переводе на нашу эру получается или 1548 год (7056 -- 5508) или 1547 год в пределах с сентября по декабрь включительно (7056 -- 5509). В это время Иван IV Васильевич именовался уже не князем, а царем. Следовательно, дата вызывает сомнение и подлежит проверке.
        В целях точной датировки документов надо обращать внимание на встречающиеся в них имена великих и удельных князей периода феодальной раздробленности и московских царей. Зная начальную и конечную дату правлеиия того или иного исторического лица, мы устанавливаем, укладывается ли в эти хронологические пределы подлежащая проверке дата документа. Так до нас дошла одна жалованная грамота Троице-Сергиеву монастырю от имени московского великого князя Василия Васильевича Темного, княжившего, как известно, в период с 1425 по 1462 г. В грамоте имеется дата: 15 мая 6979 г., т. е. в переводе на наше летосчисление 15 мая 1471 г. (6979 -- 5508). В это время Василий Темный уже умер, следовательно, в хронологических указаниях источника кроется какая-то ошибка.
        Пособием, к которому следует обращаться за справками, связанными с датами деятельности великих и удельных русских князей периода феодальной раздробленности, является труд А. В. Экземплярского: "Великие и удельные князья Северной Руси в Татарский период с 1238 по 1505 г.", т. 1-2, Спб., 1889--1891 г.
        Средством для проверки дат в руках историка оказываются также косвенные хронологические данные, относящиеся к упоминаемым в документах именам всевозможных игуменов, архимандритов, митрополитов и др. представителей церковной иерархии. Церковные организации (митрополичья кафедра, монастыри) наиболее ревниво и бережно хранили свои архивы и поэтому многие из сохранившихся до нашего времени исторических документов феодальной эпохи относятся именно к церковным феодалам. Для справок по поводу дат деятельности отдельных представителей церковной администрации, с которыми связаны те или иные акты, служит классическая работа П. М. Строева: "Списки иерархов и настоятелей монастырей Российской церкви", Спб., 1877.
        Необходимым справочником для проверки хронологических дат является также труд А. П. Барсукова: "Списки городовых воевод и других лиц воеводского управления", Спб., 1902 г.
        Существуют в русской исторической литературе и другие труды, дающие сводку данных о дьяках различных приказов, воеводах и т. д. Подобные сводки являются очень важным справочным материалом, к которому естественно должен обращаться каждый, кто ведет работу по изучению древне-русских актов. Нет возможности, да и надобности, перечислить все пособия подобного рода. Важно было наметить лишь пути проверки вызывающих сомнения дат. В качестве библиографического справочника, в котором имеются подробные ссылки на научные работы, могущие быть использованными в целях проверки неточных документальных хронологических данных, следует назвать классический "Опыт русской историографии" В. С. Иконникова (т. 1-2, в четырех выпусках).

-71-

При работе над актовым материалом, под рукой у исследователя должно обязательно быть многотомное "Полное собрание русских летописей", изданное Археографической Комиссией. Часто в актах упоминаются различные исторические события, данные которых уточняются по летописям. Пользование "Полным собранием русских летописей" облегчается наличием соответственных указателей (географического, личного и предметного). Указатели к 8 первым томам изданы отдельно. В дальнейшим томах указатели даются в отдельности каждому летописному своду, в конце его.
        Вот, например, одна жалованная грамота в кн. московского Василия Дмитриевича Троице-Сериеву монастырю дана "июль тога лета, коли город Москва погорела". А пожар в Москве в княжение Василия Дмитриевича случился, судя по летописям, 22 июля 1392 г. В другом случае грамота того же князя Василия Дмитриевича совпала с моментом выдачи княжеской дочери Анны замуж за греческого (византийского) царевича Иоанна: "А дан грамота, коли князь великий княжну отдал во Царь(град) на ту зиму на вербницю". Летописи датируют свадьбу 1411 г. Все это служит основанием дли уточнения дат.
        Историк также обязан по ряду косвенных признаков вскрыть корень ошибки, имеющейся в цифровых данных документа, и устранить ее.
        Приведем очень показательный пример с исторической проверкой дат. Одним из интереснейших памятников древнерусского права является так называемая Псковская Судная Грамота. Это -- законодательный сборник, принятый на вече в городе Пскове, как указывает заголовок Грамоты, в 6905 (‡SЦЕ) году. При переводе этой даты на нашу эру мы получим 1397 год (6906 --5508). Между тем в тексте Псковской Судной Грамоты указано, что в ее утверждении участвовали попы пяти соборов. А из летописей известно, что пятый собор возник только в 1462 г. Дата памятника, таким образом, не вяжется с его содержанием. И вот исследователи делают весьма правдоподобное предположение, что правильное цифровое обозначение года возникновения Псковской Судной Грамоты было искажено переписчиком первоначального текста. Именно, в оригинале, повидимому, была дата 6975 (‡SЦОЕ), т. е. 1467 г. нашей эры (6975 -- 5608). При переписке буква "О", обозначавшая цифру 70, была опущена. Таким образом, получилась неверная дата: 6905 = 1397 г., т. е. произошла ошибка в датировке памятника на 70 лет.
         § 3. Неточности хронологических данных древне-русских летописей и их проверка. Говоря о привлечении летописей для проверки актовой хронологии, надо в то же время учитывать, что и летописные хронологические данные часто грешат неточностями. Это относится в особенности к Начальной летописи, -- наиболее раннему дошедшему до нас памятнику летописного типа. Исследованиями ряда специалистов (главным образам, акад. Шахматова) доказано, что первоначальный древнейший текст Начальной летописи (или же не дошедших до нас предшествовавших ей летописных сводов) в основном представлял собой сплошное литературное изложение, лишенное хронологической сетки. Основные даты для наиболее

-72-

раннего периода вставлены уже позднейшей рукой, причем большинство дат не имеет под собой твердой почвы. Они появились в. результате различных домыслов и соображений летописного сводчика, сопоставлявшего события русской истории с известными ему из греческих источников хронологическими данными, относящимися к истории Византии. Так академик Шахматов, лучший знаток, древне-русского летописания, доказывает, что в пределах до 945 г. в Начальной летописи могут быть признаны заслуживающими доверия только три даты: 6420 (911) г. (договор Олега с Византией), 6449 (941) г. (поход Игоря на Визаитию) и 6453 (945) г. (договор Игоря с Византией). Все же остальные хронологические данные явно недостоверны, в частности 6370 (862) г., с которым летопись связывает мифическое призвание варягов и который фигурировал во всех старых учебниках по истории как начальная дата Русского государства. Шахматов выяснил, что за исходную точку своих хронологических построений летописный сводчик взял 6360 (852) год, --дату вступления на престол византийского императора Михаила, с которой он связал начало Руси: "В лето 6360 наченшу Михаилу царствовать, начя ся прозывати Русская земля". Летописец в данном случае был введен в заблуждение неверными указаниями своих греческих источников, т. к. в действительности Михаил вступил на престол не в 852, а в 842 г. Исходя из этой ошибочной начальной даты, летописный сводчик, в результате различных хронологических расчетов, внес в текст летописи и другие годы.
        Неточность летописной хронологии особенно ярко выступает на примере Галицко-Волынской летописи -- очень интересного и яркого памятника областного летописания XIII в., сохранившегося в составе так называемого Ипатьевского списка. Первоначальный текст Галицко-Волынской летописи был лишен хронологической канвы. Хронологическая сетка появилась в нем уже позже, при присоединении памятника к Киевскому своду. При этом даты были расставлены чисто механически. Исходной точкой для датировки послужил год, которым обрывался Киевский свод (6708 г.). В силу этого, в качестве начальной даты Галицко-Волынской летописи, появился 6709 г., к которому отнесена смерть знаменитого древне-русского князя Романа Мстиславича. Неверность этой даты вскрывается данными польских источников, которые приурочивают смерть Романа к 19 июля 1205 (6713) г. Так же случайно расставлены в Галицко-Волымской летописи и дальнейшие даты, которые поэтому и не заслуживают доверия.
        Отсюда ясно, насколько необходима проверка летописных хронологических данных.

 IV. ХРОНОЛОГИЯ ИСТОЧНИКОВ ПО ИСТОРИИ НАРОДОВ СССР

         § 1. Хронологические данные источников но истории Ливонии, Литвы, Украины, Белоруссии. В документы, относящиеся к русским территориям, которые издавна были связаны с Западом (Ливонией, Литвой и Польшей) рано проникает летосчисление по эре от "рождества христова", а также январский календарный

-73-

счет. В грамотах смоленских, галицких, полоцких и то и другое встречается уже с XIII в.
        При датировке источников по истории Ливонии надо иметь в виду, что в XIII в. там был еще в употреблении и так называемый "благовещенский" календарный счет, согласно которому новый год начинался с 25 марта (дня празднования благовещения). На основе благовещенского календарного стиля приведены, например, все даты в известной ливонской хронике Генриха Латвийского. Свой рассказ Генрих Латвийский ведет по годам епископства Альберта, посвящение которого относит к 1198 г. Когда первый издатель Хроники Грубер, иа основе этой исходной даты, рассчитал, на какие годы от "рождества христова" приходятся все другие события времени епископа Альберта, то оказалось, что хронологические данные Генриха Латвийского на год расходятся с показаниями других вполне достоверных источников. Причину этого расхождения вскрыл более поздний исследователь, Ганзен. Последний выяснил, что автор Ливонской Хроники, как и большинство западных средневековых писателей, начинал год не с 1-го янтаря, а с 25 марта, при чем этот благовещенский год отставал от современного январского календарного года на 2 месяца 24 дня. Посвящение Альберта произошло, по рассказу Хроники, весной (в феврале или начале марта) 1198 г. В переводе с благовещенского на январский календарный счет, это будет 1199 г. нашей эры. Исходя из этой даты, следует производить и все дальнейшие хронологические выкладки касательно событий, расположенных в Хронике по годам епископства Альберта. Тогда все недоразумения исчезнут.
        С XIII в. в Ливонии завоевывают преобладание новые календарные стили: декабрьский рождественский (новогодие -- 25 декабря, в день празднования рождества) и январский (новогодйе -- 1 января).
        Все вышеизложенное касательно хронологических данных, встречающихся в источниках по истории Ливонии, представляет для нас интерес в силу того, что аналогичные хронологические данные мы находим и в русских письменных памятниках, касающихся русско-ливонских взаимоотношений. Так уже выше было отмечено, что начиная с XIII в. в смоленских, полоцких и. др. западно-русских документах попадаются даты по современной эре (от "рождества христова" или говоря словами источников: "по божью нароженью", или "от воплощения господня"). Календарный стиль в большинстве случаев -- январский. Характерное для русско-ливонских документов наличие ссылок на подвижные или неподвижные праздники дает возможность произвести проверку даты. Вот один из ранних примеров датировки по нашей эре: "сию грамоту тогды написана в Ризе, коли бог был 1000 лет и 200 лет и 60 лет и 4 лета по роженьи божий за три дня", т. е. грамота относится к 22 декабря (за три дня до "рождества христова" = 25 декабря ) 1264 г. В другом документе дата сформулирована следующим образом: "по божьем нароженью 1000 лет и 400 лет и семь лет... у семую субботу месяца мая 14 день". "Семая суббота" -- это, очевидно, суббота на седьмой неделе после пасхи.

-74-

В 1407 г., как это легко установить по таблицам 1), суббота на седьмой неделе после пасхи, действительно, падала на 14 мая. Приведем последний пример: "в понедельник перед святого Семивона днем летопроводьця, по божью нароженью 1000 лет и четыре сот и 9 лет". День Семена летопроводца приходится на 1 сентября. В 1409 г. 1-сентября было воскресенье (см. таблицы IX--X). Следовательно, понедельник перед Семеновым днем = 26 августа.
        Во всех приведенных случаях -- перед нами январский календарный счет. Но если бы даже мы имели здесь дело с какими-либо другими календарными системами (благовещенской или рождественской), то это обстоятельство не внесло бы никаких изменений в установленные выше даты. Дело в том, что время составления всех документов падало на такие месяцы, для которых разница в календарных стилях не имеет значения (после 25 марта и до 25 декабря). Но если нам встретится источник из области русско-ливонских взаимоотношений, датированный временем в пределах с 1 января до 25 марта или же с 25 декабря до 1 января, то в данном случае мы обязаны предвидеть возможность того, что календарный счет этого памятника отличен от нашето. Здесь поэтому необходимо по каким-либо дополнительным признакам (например, по указаниям на праздники или дни недели) точно выяснить, с каким календарем мы имеем дело (январским, рождественским или благовещенским).
        Очень рано начинают встречаться даты от "рождества христова" по январскому стилю и в ряде документов, вошедших в состав Литовской метрики. Одновременно применяются обе системы датировки (и византийская, и современная). Характерной особенностью хронологических данных актового материала Литовской метрики является частое употребление индиктов. Надо помнить, что в том случае, когда индикт сопровождает дату от "рождества христова", для его проверки необходимо эту дату предварительно перевести на византийскую эру (по сентябрьскому календарному стилю). Например, одна из грамот дана "в лето после Христова нароженья тысеча и четыреста и 27 лета, сентября у 7 день, индикта у 6-й". 7 сентября 1427 г. н. э. соответствует 7 сентября 6936 г. (1427 + 5509) от "сотворения мира". Индикт 6936 (сентябрьского) года действительно = 6, т. к. от деления 6936 на 15 получается остаток, равный 6.
        Очень часто в актах Литовской метрики помечается один только индикт, а год отсутствует. В этом случае, руководствуясь какими-либо косвенными признаками (главным образом, упоминаемыми в документе именами), устанавливаем хронологические пределы возможного появления документа, а в этих пределах по индикту уточняем год. Например, имеется грамота, выданная в кн. литовским Казимиром Ягеллоном: "марта одиннадцатый день, индикт десятый". Выясив по какому-либо справочнику (хотя бы по энциклопедическому словарю Брокгауза -- Ефрона), что грамота падает на время между 1440 и 1447 годами, т. к. с 1447 г. Казимир
        ___________
        1) См. таблицы IX--X и XV--XVI.

-75-

Ягеллон стал уже польским королем, мы затем (по таблице V --способ был указан выше) убеждаемся, что из указанных восьми лет 10-й индикт мог соответствовать только 1447 г.
        При изучении источников по истории Украины и Белоруссии следует учитывать также, что в конце XVI в. в Польше был введен Григорианский календарь. Но по присоединении Украины и Белоруссии к России, там снова входит в употребление календарь Юлианский.
         § 2. Древне-грузинское летосчисление. В основу древне-грузинского летосчисления положен 532-х летний цикл, соответствующий русскому великому индиктиону. Этот период в 532 года носит название хроникон, причем последним термином обозначается не только самый цикл, но и то порядковое место, которое занимает данный год в пределах этого цикла. Грузинской эрой является так называемое "сотворение мира". От этой эры ведется счет и хрониконоы, и календарных годов, равных по своей продолжительности Юлианским годам. Таким образом, грузинские даты содержат двойное указание: на порядковый номер года от "сотворения мира" и на порядковый номер года в пределах текущего 532-х летнего цикла. Например: 6686 г., хроникон 302 (т. е. порядковый номер в текущем хрониконе). От "сотворения мира" до "рождества христова" грузинская хронология считает 5604 года. Значит для перевода даты на нашу эру из 6686 надо вычесть 5604. Таким образом, 6686 грузинский год соответствует 1082 г. (6686 -- 5604) н. э. Для вычисления номера года (в хрониконе) цифровое обозначение грузинской даты следует разделить на 532 и взять остаток. 6686 : 532 = 12 и 302 в остатке. Следовательно, 6686 грузинский год занимает 302-е порядков место в текущем (тринадцатом) 532-х летнем цикле.
        При расчете хрониконов по эре Дионисия надо исходить из того, что 249 год, от "рождества христова" был 1-м в 12-м цикле от "сотворения мира". Поэтому для определения хроникона любой даты нашей эры надо предварительно отнять от нее цифру 248, а разность разделить на 532. Частное в сумме с 12 покажет номер текущего цикла (хроникон), а остаток -- порядковый номер года внутри этого цирола (иногда также обозначаемый термином: хроникон). Так 1082 г. н. э. является 302-м в 13-м хрониконе (1082 --248 = 834; 834 : 532 = 1; 1 + 12 = 13; остаток от деления 834 на 532 = 302).
        Ниже помещена таблица XXI, пользуясь которой, можно без всяких вычислений установить соответствие дат по грузинскому и современному европейскому летосчислению.
        Таблица построена следующим образом. В левой вертикальной графе помещены сверху тысячелетия и столетия, а ниже десятки и единицы годов грузинской эры от "сотворения мира". В правой вертикалынюй графе расположены (по тому же принципу) соответствующие грузинским даты нашей эры. Между двумя названными крайними колонками цифр находятся четыре графы, заключающие в себе хронологические данные по четырем хрониконам: 12 -- 15

 Таблица XXI

Перевод дат с древне-грузинского летосчисления на современное европейское

От "сотво-
рения мира"

Хрониконы

От "рож-
дества
христова"

12 (1)

13 (2)

14 (3)

15 (4)

 

75

 

 

 

 

 

0    1

19

С
о
т
н
и

л
е
т

 

74

 

 

 

         4

5

        0

18

73

 

 

 

3        4

 

 

17

72

 

 

 

2        3

 

 

16

71

 

 

 

1        2

 

 

15

70

 

 

 

0        1

 

 

14

69

 

 

5

0

 

 

13

68

 

4

 

 

 

 

12

67

 

3

 

 

 

 

11

66

 

2

 

 

 

 

10

65

 

1

 

 

 

 

9

64

 

0

 

 

 

 

8

63

4        5

 

 

 

 

 

7

62

3        4

 

 

 

 

 

6

61

2        3

 

 

 

 

 

5

60

1        2

 

 

 

 

 

4

59

0        1

 

 

 

 

 

3

58

        0

 

 

 

 

 

2

57

 

 

 

 

 

 

1

56

 

 

 

 

 

 

0

 

Д
е
с
я
т
к
и

л
е
т
 

04

52

20

20

88

 

56

00

Д
е
с
я
т
к
и

л
е
т

05

53

21

21

89

 

57

01

06

54

22

22

90

 

58

02

07

55

23

23

91

 

59

03

08

56

24

24

92

 

60

04

09

57

25

25

93

 

61

05

10

58

26

26

94

 

62

06

11

59

27

27

95

 

63

07

12

60

28

28

96

 

64

08

13

61

29

29

97

 

65

09

14

62

30

30

98

 

66

10

15

63

31

31

99

 

67

11

16

64

32

32

00

00

68

12

17

65

33

 

01

01

69

13

18

66

34

 

02

02

70

14

19

67

35

 

03

03

71

15

20

68

36

 

04

04

72

16

21

69

37

 

05

05

73

17

22

70

38

 

06

06

74

18

23

71

39

 

07

07

75

19

24

72

40

 

08

08

76

20

25

73

41

 

09

09

77

21

26

74

42

 

10

10

78

22

27

75

43

 

11

11

79

23

28

76

44

 

12

12

80

24

29

77

45

 

13

13

81

25

30

78

46

 

14

14

82

26

31

79

47

 

15

15

83

27

32

80

48

 

16

16

84

28

33

81

49

 

17

17

85

29

34

82

50

 

18

18

86

30

35

83

51

 

19

19

87

31

36

84

52

 

20

20

88

32

37

85

53

 

21

21

89

33

38

86

54

 

22

22

90

34

39

87

55

 

23

23

91

35

40

88

56

 

24

24

92

36

41

89

57

 

25

25

93

37

42

90

58

 

26

26

94

38

43

91

59

 

27

27

95

39

44

92

60

 

28

28

96

40

45

93

61

 

29

29

97

41

46

94

62

 

30

30

98

42

47

95

63

 

31

31

99

43

48

96

64

 

32

32

00

44

49

97

65

 

33

 

01

45

50

98

66

 

34

 

02

46

51

99

67

 

35

 

03

47

52

00

68

 

36

 

04

48

53

01

69

 

37

 

05

49

 Таблица XXI (вторая половина)

Перевод дат с древне-грузинского летосчисления на современное европейское

От "сотво-
рения мира"

Хрониконы

От "рождест-
ва христова"

12 (1)

13 (2)

14 (3)

15 (4)

 

75    76

 

 

 

 

1

19

С
о
т
н
и

л
е
т

 

74    75

 

 

 

 

0

18

73    74

 

 

 

4

 

17

72    73

 

 

 

3

 

16

71    72

 

 

 

2

 

15

70    71

 

 

 

1

 

14

69    70

 

 

 

0

 

13

68    69

 

 

4    5

 

 

12

67    68

 

 

3    4

 

 

11

66    67

 

 

2    3

 

 

10

65    66

 

 

1    2

 

 

9

64    65

 

 

0    1

 

 

8

63    64

 

5

     0

 

 

7

62    63

4

 

 

 

 

6

61    62

3

 

 

 

 

5

60    61

2

 

 

 

 

4

59    60

1

 

 

 

 

3

58    59

0

 

 

 

 

2

57    58

 

 

 

 

 

1

56    57

 

 

 

 

 

0

 

Д
е
с
я
т
к
и

л
е
т
 

54

02

02

70

38

06

50

Д
е
с
я
т
к
и

л
е
т

55

03

03

71

39

07

51

56

04

04

72

40

08

52

57

05

05

73

41

09

53

58

06

06

74

42

10

54

59

07

07

75

43

11

55

60

08

08

76

44

12

56

61

09

09

77

45

13

57

62

10

10

78

46

14

58

63

11

11

79

47

15

59

64

12

12

80

48

16

60

65

13

13

81

49

17

61

66

14

14

82

50

18

62

67

15

15

83

51

19

63

68

16

16

84

52

20

64

69

17

17

85

53

21

65

70

18

18

86

54

22

66

71

19

19

87

55

23

67

72

20

20

88

56

24

68

73

21

21

89

57

25

69

74

22

22

90

58

26

70

75

23

23

91

59

27

71

76

24

24

92

60

28

72

77

25

25

93

61

29

73

78

26

26

94

62

30

74

79

27

27

95

63

31

75

80

28

28

96

64

32

76

81

29

29

97

65

33

77

82

30

30

98

66

34

78

83

31

31

99

67

35

79

84

32

32

00

68

36

80

85

33

 

01

69

37

81

86

34

 

02

70

38

82

87

35

 

03

71

39

83

88

36

 

04

72

40

84

89

37

 

05

73

41

85

90

38

 

06

74

42

86

91

39

 

07

75

43

87

92

40

 

08

76

44

88

93

41

 

09

77

45

89

94

42

 

10

78

46

90

95

43

 

11

79

47

91

96

44

 

12

80

48

92

97

45

 

13

81

49

93

98

46

 

14

82

50

94

99

47

 

15

83

51

95

00

48

 

16

84

52

96

01

49

 

17

85

53

97

02

50

 

18

86

54

98

53

51

 

19

87

55

99

-76-

от "сотворения мира" или (что то же) 1--4 от "рождества христова".
        Порядковый номер того или иного года внутри каждого хроникона складывается из цифрового обозначения сотен, указанного наверху (на одной линии со столетиями самой даты) и десятков и единиц, которые обозначены ниже, против десятилетий и единиц годов соответствующей даты.
        При пользовании таблицей надо только обязательно наблюдать строгое соответствие в пределах различных граф цифр, (выделенных курсивом -- с одной стороны, и обычных -- с другой).
         § 3. Древне-армянское летосчисление. Продолжительность древне-армянского года была принята равной 365 суткам. Таким образом, армянский календарный год был немного короче солнечного (тропического), равного 365,2422 суток. Календарный год делился на 12 месяцев по 30 дней в каждом, три чем в конце года прибавлялось еще 5 дополнительных дней (30 * 12 + 5 = 365). Месяцы носили следующие названия: навасарди, хори, сахми, тре, кхалоц, арац, мехекани, арег, ахекани, марери, доаргац, хротиц.
        По своей структуре древне-армянский календарь воспроизводил одну из древнейших календарных систем -- египетскую. Египетский календарь, как мы видели вначале, также исходил из постоянного количества дней в году (= 365) и, в противоположность Юлианскому календарю, не знал високосных годов. Так же, как и армянский, древне-египетский год складывался из 12 тридцатидневных месяцев 1) с добавлением по их окончании еще 5 лишних дней. И древне-египетский и древне-армянский календари в одинаковой мере убегали вперед по сравнению с Юлианским. Отставание последнего достигало одних суток в четырехлетний период, т. к. из каждых четырех Юлианских лет один был високосным ( = 366, а не 365 суткам). Вследствие этого, египетское и армянское новогодие последовательно передвигались (с интервалами через каждое четырехлетие) по всем месяцам и дням Юлианского года, при чем в направлении, обратном их естественной последовательности. За 1460 лет египетский и армянский календари опережали Юлианский на целый год ( = 365 суткам). Действительно, исходя из нарастающей разницы между календарями (египетским и армянским -- с одной стороны, Юлианским -- с другой) в количестве одних суток за четырехлетие, разница в 365 суток наступит через 1460 лет. Другими славами, 1460 египетских или армянских лет = 1461 Юлианскому году. Через 1460 лет начало египетского или армянского года, обойдя последовательно (в обратном порядке) все числа Юлианского календаря, возвращается, на исходное число. Этот промежуток в 1460 лет древние египтяне, как мы знаем, называли "Софическим периодом" или "периодом Сотиса".
        В качестве эры, в древне-армянской хронологии фигурирует дата 11 июля 552 г. европейского летосчисления. Другая армянская
        ___________
        1) Их названия отличались от армянских.

-77-

хронологическая система берет за свою исходную точку дату на год позже (11 июля 553 г.). Таким образом, приходится говорить о двух видах древнеармяиского летосчисления и при пользовании армянскими источниками предварительно необходимо установить, по какой именно системе они датированы. Большею частью даты даются по счету от 11 июля 552 г. Поэтому дальнейшие указания по поводу перевода армянских хронологических данных на современное летосчисление будут даны применительно к этой эре.
        Если в 552 г. современной эры, когда началось армянское летосчисление, армянское новогодие (1-ое навасарди 1-го года) совпало с 11 июля Юлианского календаря, то через четыре года (в 556 г. н. э.) оно придется на 10 июля, через восемь лет (в 560 г. н. э.) --на 9 июля, через 12 лет (в 564 г. н. э.) -- на 8 июля и т. д. ..., через 1460 лет (в 2012 г. н. э.) -- снова на 11 июля 1). Поэтому, когда мы встречаем в источнике какую-либо армянскую дату (например, 5 хротиц 835 г.), то для ее перевода на европейское летосчисление мы прежде всего должны установить, на какое число, месяц и год Юлианского календаря падает начало (1-ое навасарди) интересующего нас армянского года. Мы знаем, что армянской эрой является 11 июля 552 г. Поэтому, если бы армянский календарный год по своей продолжительности был равен Юлианскому, то новогодие (1-ое навасарди) армянского 835 г. совпало бы с 11 июля 1387 г. Действительно, 11 июля 552 г. (армянская эра) + 835 = 11 июля 1387 г. Но (поскольку армянский год короче Юлианского, нам необходимо выяснить, на сколько суток армянский календарь опередил Юлианский за время до наступления той армянской даты, которую мы рассматриваем (835 г.). Если за каждые четыре года разница между армянским и Юлианским календарями выражается в одних сутках, то за 835 лет она достигнет 208 суток (835 : 4 = = 208, остаток отбрасываем). Учитывая подобное отставание Юлианского календаря, мы естественно должны внести поправку в ту дату (11 июля 1387 г.), которая получилась в результате предварительного перевода 835 г. армянской эры без учета (разницы двух календарей. Очевидно, начало 835 армянского года совпадет не с 11 июля 1357 г. н. э., а с датой, имевшей место на 208 суток ранее 11 июля 1357 г. - 208 суток = 15 декабря 1356г. Если 1 навасарди 835 армянского года соответствует 15 декабря 1386 г. н. э., то зная это, уже не трудно произвести перевод на нашу эру даты 5 хротиц 835 г. армянской эры. Для этого следует вычислить, каким по счету днем от начала армянского года (от 1-го навасарди) является 5 число месяца хротиц и отсчитать найденное количество дней от 15 декабря 1386 г. н. э. ( = 1 навасарди 835 г. армянского летосчисления). 5 хротиц -- 335-й день от начала армянского года. 15 декабря 1386 г. + 335 суток = 15 ноября 1387 г.
        Общая формула перевода дат с древне-армянского летосчисления на современное может быть выражена следующим образом:
        X = (11 июля 552 г. + N) - N4 суток + Т.
        ___________
        1) В 553--555 гг., как и в 552 г. новый армянский год будет 11 июля, в 559--559 -- 10 июля и т. д.

 Таблица XXII

Перевод дат с древне-армянского летосчисления на современное европейское

С о т н и   л е т

Десятки
и 
единицы
лет
армянской
эры

С о т н и   л е т

Десятки
и 
единицы
лет
армянской
эры

Эры "от
рождества
христова"

6

7

8

9

10

11

12

13

13

14

15

16

17

18

19

Армянской
эры

0

1

2

3

4

5

6

7

7

8

9

10

11

12

13

Десятки и
единицы
лет эры "от
рождества
христова"

1-й день начинающегося года

1-й день начинающегося года

Июнь

Июнь

Май

Апрель

Март

Февраль

Января

Январь

 

Декабрь

Ноябрь

Октябрь

Сентябрь

Сентябрь

Август

00

29

4

10

15

21

25

31

6

49

 

11

16

22

27

2

8

50

01

29

4

10

15

21

24

30

5

50

 

11

16

22

27

2

8

51

02

29

4

10

15

21

24

30

5

51

 

11

16

22

27

2

8

52

03

29

4

10

15

21

24

30

5

52

 

11

16

22

27

2

8

53

04

28

3

9

14

20

24

30

5

53

 

10

15

21

26

1

7

54

05

28

3

9

14

20

23

29

4

54

 

10

15

21

26

1

7

55

06

28

3

9

14

20

23

29

4

55

 

10

15

21

26

1

7

56

07

28

3

9

14

20

23

29

4

56

 

10

15

21

26

1 Сент.

7

57

08

27

2

8

13

19

23

29

4

57

 

9

14

20

25

31 Авг.

6

58

09

27

2

8

13

19

22

28

3

58

 

9

14

20

25

31

6

59

10

27

2

8

13

19

22

28

3

59

 

9

14

20

25

31

6

60

11

27

2

8

13

19

22

28

3

60

 

9

14

20

25

31

6

61

12

26

1

7

12

18

22

28

3

61

 

8

13

19

24

30

5

62

13

26

1

7

12

18

21

27

2

62

 

8

13

19

24

30

5

63

14

26

1

7

12

18

21

27

2

63

 

8

13

19

24

30

5

64

15

26

1 Июнь

7

12

18

21

27

2

64

 

8

13

19

24

30

5

65

16

25

31 Май

6

11

17

21

27

2

65

 

7

12

18

23

29

4

66

17

25

31

6

11

17

20

26

1

66

 

7

12

18

23

29

4

67

18

25

31

6

11

17

20

26

1

67

 

7

12

18

23

29

4

68

19

25

31

6

11

17

20

26

1

68

 

7

12

18

23

29

4

69

20

24

30

5

10

16

20

26

1

69

31

6

11

17

22

28

3

70

21

24

30

5

10

16

19

25->

 

70

31

6

11

17

22

28

3

71

22

24

30

5

10

16

19

25->

 

71

31

6

11

17

22

28

3

72

23

24

30

5

10

16

19

25->

 

72

31

6

11

17

22

28

3

73

24

23

29

4

9

15

19

25->

 

73

30

5

10

16

21

27

2

74

25

23

29

4

9

15

18

24->

 

74

30

5

10

16

21

27

2

75

26

23

29

4

9

15

18

24->

 

75

30

5

10

16

21

27

2

76

27

23

29

4

9

15

18

24->

 

76

30

5

10

16

21

27

2

77

28

22

28

3

8

14

18

24->

 

77

29

4

9

15

20

26

1

78

29

22

28

3

8

14

17

23->

 

78

29

4

9

15

20

26

1

79

30

22

28

3

8

14

17

23->

 

79

29

4

9

15

20

26

1

80

31

22

28

3

8

14

17

23->

 

80

29

4

9

15

20

26

1 Август

81

32

21

27

2

7

13

17

23->

 

81

28

3

8

14

19

25

31 Июль

82

33

21

27

2

7

13

16

22->

 

82

28

3

8

14

19

25

31

83

34

21

27

2

7

13

16

22->

 

83

28

3

8

14

19

25

31

84

35

21

27

2

7

13

16

22->

 

84

28

3

8

14

19

25

31

85

36

20

26

1

6

12

16

22->

 

85

27

2

7

13

18

24

30

86

37

20

26

1

6

12

15

21->

 

86

27

2

7

13

18

24

30

87

38

20

26

1

6

12

15

21->

 

87

27

2

7

13

18

24

30

88

39

20

26

1 Май

6

12

15

21->

 

88

27

2

7

13

18

24

30

89

40

19

25

30 Апр.

5

11

15

21->

 

89

26

1

6

12

17

23

29

90

41

19

25

30

5

11

14

20->

 

90

26

1

6

12

17

23

29

91

42

19

25

30

5

11

14

20->

 

91

26

1

6

12

17

23

29

92

43

19

25

30

5

11

14

20->

 

92

26

1 Дек.

6

12

17

23

29

93

44

18

24

29

4

10

14

20->

 

93

25

30 Нояб.

5

11

16

22

28

94

45

18

24

29

4

10

13

19->

 

94

25

30

5

11

16

22

28

95

46

18

24

29

4

10

13

19->

 

95

25

30

5

11

16

22

28

96

47

18

24

29

4

10

13

19->

 

96

25

30

5

11

16

22

28

97

48

17

23

28

3

9

13

19->

 

97

24

29

4

10

15

21

27

98

49

17

23

28

3

9

12

18->

 

98

24

29

4

10

15

21

27

99

Эра "от
рождества

христова"

Июнь

Май

Апрель

Апрель

Март

Февраль

Январь

 

Армян.
эра

Декабрь

Ноябрь

Ноябрь

Октябрь

Сентябрь

Август

Июль

Армян.
эра

1-й день начинающегося года

1-й день начинающегося года

 Таблица XXII (вторая половина)

Перевод дат с древне-армянского летосчисления на современное европейское

С о т н и   л е т

Десятки
и 
единицы
лет
армянской
эры

С о т н и   л е т

Десятки
и 
единицы
лет
армянской
эры

Эры "от
рождества
христова"

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

Армянской
эры

0

1
0

2
1

3
2

4
3

5
4

6
5

7
6

8

9

10

11

12

13

14

Десятки и
единицы
лет эры "от
рождества
христова"

1-й день начинающегося года

1-й день начинающегося года

Июль

Июнь

Май

Апрель

Апрель

Март

Февраль

Январь

 Декабрь

Ноябрь

Ноябрь

Октябрь

Сентябрь

Август

Июль

50

--

17

23

28

3

9

12

18

99

24

29

4

10

15

21

27

00

51

--

17

23

28

3

9

12

18

00

24

29

4

10

15

21

27

01

52

11

16

22

27

2

8

12

18

01

23

28

3

9

14

20

26

02

53

11

16

22

27

2

8

11

17

02

23

28

3

9

14

20

26

03

54

11

16

22

27

2

8

11

17

03

23

28

3

9

14

20

26

04

55

11

16

22

27

2

8

11

17

04

23

28

3

9

14

20

26

05

56

10

15

21

26

1

7

11

17

05

22

27

2

8

13

19

25

06

57

10

15

21

26

1

7

10

16

06

22

27

2

8

13

19

25

07

58

10

15

21

26

1

7

10

16

07

22

27

2

8

13

19

25

08

59

10

15

21

26

1 Апр.

7

10

16

08

22

27

2

8

13

19

25

09

60

9

14

20

25

31 Март

6

10

16

09

21

26

1

7

12

18

24

10

61

9

14

20

25

31

6

9

15

10

21

26

1

7

12

18

24

11

62

9

14

20

25

31

6

9

15

11

21

26

1

7

12

18

24

12

63

9

14

20

25

31

6

9

15

12

21

26

1 Нояб.

7

12

18

24

13

64

8

13

19

24

30

5

9

15

13

20

25

31 Окт.

6

11

17

23

14

65

8

13

19

24

30

5

8

14

14

20

25

31

6

11

17

23

15

66

8

13

19

24

30

5

8

14

15

20

25

31

6

11

17

23

16

67

8

13

19

24

30

5

8

14

16

20

25

31

6

11

17

23

17

68

7

12

18

23

29

4

8

14

17

19

24

30

5

10

16

22

18

69

7

12

18

23

29

4

7

13

18

19

24

30

5

10

16

22

19

70

7

12

18

23

29

4

7

13

19

19

24

30

5

10

16

22

20

71

7

12

18

23

29

4

7

13

20

19

24

30

5

10

16

22

21

72

6

11

17

22

28

3

7

13

21

18

23

29

4

9

15

21

22

73

6

11

17

22

28

3

6

12

22

18

23

29

4

9

15

21

23

74

6

11

17

22

28

3

6

12

23

18

23

29

4

9

15

21

74

75

6

11

17

22

28

3

6

12

24

18

23

29

4

9

15

21

25

76

5

10

16

21

27

2

6

12

25

17

22

28

3

8

14

20

26

77

5

10

16

21

27

2

5

11

26

17

22

28

3

8

14

20

27

78

5

10

16

21

27

2

5

11

27

17

22

28

3

8

14

20

28

79

5

10

16

21

27

2

5

11

28

17

22

28

3

8

14

20

29

80

4

9

15

20

26

1

5

11

29

16

21

27

2

7

13

19

30

81

4

9

15

20

26

1

4

10

30

16

21

27

2

7

13

19

31

82

4

9

15

20

26

1

4

10

31

16

21

27

2

7

13

19

32

83

4

9

15

20

26

1 Март

4

10

32

16

21

27

2

7

13

19

33

84

3

8

14

19

25

29 Фев.

4

10

33

15

20

26

1

6

12

18

34

85

3

8

14

19

25

28

3

9

34

15

20

26

1

6

12

18

35

86

3

8

14

19

25

28

3

9

35

15

20

26

1

6

12

18

36

87

3

8

14

19

25

28

3

9

36

15

20

26

1 Окт.

6

12

18

37

88

2

7

13

18

24

28

3

9

37

14

19

25

30 Сент.

5

11

17

38

89

2

7

13

18

24

27

2

8

38

14

19

25

30

5

11

17

39

90

2

7

13

18

24

27

2

8

39

14

19

25

30

5

11

17

40

91

2

7

13

18

24

27

2

8

40

14

19

25

30

5

11

17

41

92

1

6

12

17

23

27

2

8

41

13

18

24

29

4

10

16

42

93

1

6

12

17

23

26

1

7

42

13

18

24

29

4

10

16

43

94

1

6

12

17

23

26

1

7

43

13

18

24

29

4

10

16

44

95

1 Июль

6

12

17

23

26

1

7

44

13

18

24

29

4

10

16

45

96

30 Июнь

5

11

16

22

26

1 Фев.

7

45

12

17

23

28

3

9

15

46

97

30

5

11

16

22

25

31 Янв.

6

46

12

17

23

28

3

9

15

47

98

30

5

11

16

22

25

31

6

47

12

17

23

28

3

9

15

48

99

30

5

11

16

22

25

31

6

48

12

17

23

28

3

9

15

49

Эра "от
рождества

христова"

Июнь

Июнь

Май

Апрель

Март

Февраль

Январь

Январь

Армян.
эра

Декабрь

Ноябрь

Ноябрь

Октябрь

Сентябрь

Август

Июль

Армян.
эра

1-й день начинающегося года

1-й день начинающегося года

-78-

        Под N подразумевается цифровое обозначение года армянской эры, под Т -- количество дней от начала армянского года до данной для перевода даты включительно. X -- искомая дата современного летосчисления.
        Первую часть вычислений, именно перевод на наше летосчисление армянского новогодия, можно упростить, прибегнув к специальной таблице XXII, помещаемой ниже. В верхних графах двух половин таблицы дано соответствие столетий армянской и современной европейской эры. Десятки и единицы армянских годов расположены сверху вниз в правых вертикальных графах (в обеих половинах таблицы по пятидесятилетию). Соответствующие армянской дате десятки и единицы Юлианских годов находятся в крайней левой вертикальной графе. Пересечение перпендикуляра, опущенного сверху вниз от столетий армянского летосчисления, и горизонтали, проведенной справа налево от десятков и единиц интересующей нас армянской даты, укажет месяц и число Юлианского календаря, на которое приходится армянское новогодие (I навасарди). Установив последнее, легко уже указанным выше способом вычислить любую дату, относящуюся к середине года.
         § 4. Мусульманское летосчисление. В основу мусульманского календаря положен свободный лунный год. Этим термином, как было указано выше, принято называть календарный год, состоящий из 12 лунных месяцев. Длина синодического лунного месяца равна, как мы знаем, 29,5306 суток, или около 29,5 суток. Исходя из этой округленной средней цифры, продолжительность 12-ти месячного лунного года выразится в 354 сутках (29,5 * 12). Однако, явно неудобно при календарном счете приравнивать месяц неполному количеству суток. Поэтому мусульманский год строится на чередовании так называемых полных месяцев (содержащих каждый по 30 суток) и пустых (содержащих по 29 суток). 6 месяцев по 30 суток и 6 -- по 29 суток в сумме дают то же количество суток (354), которое получается из расчета средней продолжительности месяца в 29,5 суток.
        Наименования мусульманских месяцев и количество дней в каждом из них указаны в следующей таблице XXIII. В ней дано также количество дней, прошедших от мусульманского новогодия до первого числа каждого месяца.

 Таблица XXIII

Мусульманский календарный год

Месяцы

Мухаррам
(30)

Сафар
(29)

Реби I
(30)

Реби-II
(29)

Джумади-I
(30)

Джумади-II
(29)

Раджаб
(30)

Шабан
(29)

Рамазан
(30)

Шавалль
(29)

Зу-л-каде
(30)

Зу-л-хидже
(29 или 30)

Числа дней до первого числа

-

30

59

89

118

148

177

207

236

266

295

325

-79-

        Как видно из таблицы, нечетные месяцы мусульманского года (1-ый, 3-й, 5-й и т. д.) содержат по 30 суток, а четные (2-й, 4-й, 6-й и т. д.) -- по 29.
        Принятая в мусульманском лунном календаре длина месяца в 29,5 суток меньше действительной продолжительности лунного синодического месяца (= 29,5306). Таким образом, мусульманский календарный год заканчивается ранее завершения лунного года, складывающегося из 12-ти синодических лунных месяцев. Другими словами, начало календарных месяцев перестает приходиться на определенную фазу луны. За период в 30 лет разница между мусульманским календарным и синодическим лунными годами нарастает уже до 11 суток. Действительно:
        29,5 х 12 х 30 == 10620 суток.
        29,5306 х 12 х 30 = 10631 суток.
        10631 - 10620=11 суток.
        Для устранения указанной разницы было необходимо внести в мусульманский календарь 11 дополнительных дней в течение каждого 30-летнего периода. Иными словами, надо было в пределах каждых 30 лет считать 19 годов простых (по 354 суток) и 11 високосных (по 355 суток). В високосных годах последний месяц имеет не 29, а 30 суток. За високосные годы в мусульманском календаре приняты: 2-й, 5-й, 7-й, 10-й, 13-й, 16-й, 18-й, 21-й, 24-й, 26-й и 29-й (в каждом 30-летнем цикле).
        Мусульманской эрой является 16 июля 622 г. (от "рождества христова") -- дата бегства основателя мусульманской религии Мухаммеда из Мекки в Медину от преследований своих противников. Мусульманская эра носит название "гиджры" (иное написание -- "геджра", "хиджра"). Это -- арабское слово, буквально означающее "бегство".
        Знание мусульманской системы летосчисления имеет большое значение для историков СССР, т. к. им пользовались миогие народы, входящие в состав Советского Союза (татары, ряд народов Крыма, Кавказа, Средней Азии).
        Для перевода дат с мусульманского летосчисления на европейское необходимо учитывать не только то обстоятельство, что мусульманский счет лет начался на 622 года позднее нашей эры. Надо обращать внимание и на то, что год лунного мусульманского календаря (= 354 или 355 суткам) в среднем на 11 суток короче солнечного года (= 365 или 366 суткам), положенного в основу календарей Юлианского и Григорианского. Европейский календарь систематически отстает от мусульманского, при чем в течение 33 лет это отставание приблизительно достигает полного солнечного года (11 х 33 = 363 дня). Другими словами, 33 мусульманских календарных года почти равны по продолжительности 32 европейским календарным годам.
        Исходя из всех этих данных, попробуем вывести общую формулу перевода любой даты с эры гиджры на европейское летосчисление. Обозначим цифровое выражение данного нам года эры гиджры буквой N, а соответствующего ему года от "рождества христова" -- буквой X. Мы знаем, что наш календарный год длиннее

-80-

мусульманского, что за 33-летний период мусульманский календарь уходит на целый солнечный год по сравнению с нашим. Следовательно, нам необходимо определить то количество лет, на которое мусульманский календарь опередит европейский в течение указанного нам периода в N-ое число лет по мусульманскому календарному счету (т. е. до той даты эры гиджры, которая подлежит переводу на летосчисление от "рождества христова"). Для этого мы должны N разделить на 33. Выражение N33 показывает отставание европейского календаря. Поэтому, чтобы узнать, сколько европейских календарных годов прошло за период в N-ое число лет по мусульманскому календарному счету, мы должны из N вычесть частное N33.
        Но с другой стороны, нам известно, что мусульманское летосчисление началось на 622 года после нашей эры. Поэтому, при переводе на последнюю, к выражению (N-N33), показывающему количество европейских календарных годов, (содержащихся в N-ом числе мусульманских лет эры гиджры, мы должны прибавить 622. Таким образом, общая формула перевода дат с эры гиджры на эру от "рождества христова" может быть выражена следующим образом:
        X= N - N33 + 622.
        Предположим, что в источнике нам указан 845 г. эры гиджры. Пользуясь выведенной формулой, следующим образом производим перевод этой даты на эру от "рождества христова": X = 845 - 84533 + 622 = 845 - 25 + 622 = 1422 год нашей эры.
        Надо сразу оговориться, что пользуясь указанной выше формулой, мы лишены возможности достигнуть абсолютной точности при переводе дат с эры гиджры на наше летосчисление. В самом деле, отставание европейского календаря мы устанавливаем лишь приблизительно, отбрасывая остаток при делении N на 33.
        Мы уже не раз говорили, что мусульманский год короче европейского, поэтому начало года не совпадает по обоим календарям и мусульманское новогодие передвигается по различным датам нашего календаря. Когда начало мусульманского года приходится на первые январские числа европейского календаря, тогда он (как менее продолжительный) и заканчивается в течение того же самого европейского календарного года. Но в большинстве случаев N-ый мусульманский год, в основном соответствующий X-му году нашего летосчисления, частично захватывает своим началом или концом и предыдущий (X - 1)-ый или же, наоборот, следующий (X + 1)-ый год. Отсюда ясно, что при пользовании формулой, раскрывающей лишь цифровое значение X, всегда надо учитывать поправку

-81-

в сторону X + 1 или X - 1, в зависимости от месяца и числа подлежащей переводу даты. Другими словами, формула ие позволяет устанавливать пределы (начало и конец) мусульманского года по европейскому календарю. Производить перевод с предельной точностью помогает специально для этой цели составленная таблица XXIV. По ней мы имеем возможность установить год, число и месяц по (нашему календарю, на которые приходится, начало того или иного года эры гиджры, а отравляясь от магометанского новогодия, перевести далее на современный календарь любые числа Мусульманских месяцев.
        В приведенной таблице, в верхних графах, дано соответствие столетий мусульманской и современней эры. Десятки и единицы годов эры гиджры расположены сверху вниз в крайней левой вертикальной графе. Проведя вертикальную линию сверху вниз, от столетий мусульманского летосчисления, и горизонтальную линию слева направо, от десятков и годов данной мусульманской даты, мы на пересечении обеих линий найдем соответствующую дату по летосчислению от "рождества христова" и месяц и число Юлианского календаря, на которое приходится мусульманское новогодие (1-е мухаррама). Далее мы определяем, сколько полных дней от начала года по Юлианскому календарю (от 1 января) прошло до найденного в таблице числа, на которое падает мусульманское новогодие. Узнаем также (по таблице мусульманских месяцев), каким днем от начала мусульманского года (от 1 мухаррама) является число того или иного мусульманского месяца, указанное в дате, подлежащей переводу на нашу эру. Складываем обе найденных величины и узнаем таким образом, каким по счету днем (считая от 1 января найденной даты, современной эры) будет интересующее нас число мусульманского месяца эры гиджры.
        Пример: требуется перевести на нашу эру дату 3 реби 1 1037 г. эры гиджры. По таблице узнаем, что на 2 сентября 1627 г. нашей эры падает 1 мухаррама 1037 г. эры гиджры. До 2 сентября от начала Юлианского года прошло полных 244 дня. 3 реби 1 -- 62-й день мусульманского года. 244 + 62 = 306. 3 реби 1 1037 г. эры гиджры = 306-й день от начала 1627 г. нашей эры, т. е. 2 ноября 1627 г.
         § 5. Тюрко-монгольское летосчисление. Тюрко-монгольский календарь представляет собой попытку установить определенную связь между лунным месяцем и солнечным годом. В основу этого соотношения было положено то наблюдение, которое в свое время было сделано в древней Греции Метоном и к которому монголы пришли независимо от него: наблюдение о том, что 19 солнечных лет содержат 235 полных лунных месяцев. Исходя из этого, тюрко-монгольская календарная система предусматривала в пределах каждого девятнадцатилетнего периода чередование 12 простых годов (по 12 месяцев) и 7 годов удлиненных (по 13 месяцев). 12 Месяцев х 12 + 13 месяцев х 7 = 235 месяцев.
        Каждый месяц имел свой порядковый номер (от 1 до 12 в обычном году). Поэтому тюрко-монгольские календарные даты

 Таблица XXIV
(первая половина)

Перевод дат с мусульманского летосчисления на современное европейское

сто-
ле-
тия

Эра от "рожд.
христова"

6

 

7

 

8

 

9

 

10

 

11

 

12

 

13

 

14
13

 

15
14

 

16
15

 

17
16

 

18
17

 

19
18

сто-
ле-
тия

Эра Гидж-
ры

0

 

1

 

2

 

3

 

4

 

5

 

6

 

7

 

8

 

9

 

10

 

11

 

12

 

13

00

 

 

3 авг.

18

11 авг.

15

18 авг.

12

25 авг.

09

2 сен.

06

10 сен.

03

16 сен.

00

24 сен.

97

2 окт.

94

9 окт.

91

16 окт.

88

24 окт.

85

31 окт.

82

01

16 июля

22

24 июля

19

30 июля

16

7 авг.

13

15 авг.

10

22 авг.

07

29 авг.

04

6 сен.

01

13 сен.

98

21 сен.

95

28 сен .

92

5 окт.

89

13 окт.

86

21 окт.

83

02

5 июля

23

12 июля

20

20 июля

17

27 июля

14

4 авг.

11

11 авг.

08

18 авг.

05

26 авг.

02

3 сен.

99

9 сен.

96

17 сен.

93

24 сен.

90

2 окт.

87

9 окт.

84

03

24 июня

24

1 июля

21

9 июля

18

17 июля

15

23 июля

12

31 июля

09

8 авг.

06

15 авг.

03

22 авг.

00

30 авг.

97

6 сен.

94

14 сен.

91

21 сен.

88

28 сен.

85

04

13 июня

25

21 июня

22

28 июня

19

5 июля

16

13 июля

13

20 июля

10

28 июля

07

4 авг.

04

11 авг.

01

19 авг.

98

27 авг.

95

2 сен.

92

10 сен.

89

18 сен.

86

05

2 июня

26

10 июня

23

17 июня

20

24 июня

17

2 июля

14

10 июля

11

16 июля

08

24 июля

05

1 авг.

02

8 авг.

99

15 авг.

96

23 авг.

93

30 авг.

90

7 сен.

87

06

23 мая

27

29 мая

24

6 июня

21

14 июня

18

21 июня

15

28 июня

12

6 июля

09

13 июля

06

21 июля

03

28 июля

00

4 авг.

97

12 авг.

94

20 авг.

91

26 авг.

88

07

11 мая

28

19 мая

2В

27 мая

22

3 июня

19

10 июня

16

18 июня

13

25 июня

10

3 июля

07

10 июля

04

17 июля

01

25 июля

98

2 авг.

95

8 авг.

92

16 авг.

89

08

1 мая

29

8 мая

26

16 мая

23

23 мая

20

30 мая

17

7 июня

14

15 июня

11

21 июня

08

29 июня

05

7 июля

02

14 июля

99

21 июля

96

29 июля

93

5 авг.

90

09

20 апр.

30

28 апр.

27

4 мая

24

12 мая

21

20 мая

18

27 мая

15

3 июня

12

11 июня

09

18 июня

00

26 нюня

03

3 июля

00

11 июля

97

18 июля

94

26 июля

91

10

9 апр.

31

16 апр.

28

24 апр.

25

1 мая

22

9 мая

19

16 мая

16

23 мая

13

31 мая

10

8 июня

07

14 июня

04

22 нюня

01

30 июня

98

7 июля

95

14 июля

92

11

29 марта

32

5 апр.

29

13 апр.

26

21 апр.

23

27апр.

20

5 мая

17

13 мая

14

20 мая

11

27 мая

08

4 июня

05

11 нюня

02

19 июня

99

26 июня

96

3 июля

93

12

18 марта

33

26 марта

30

2 апр.

27

9 апр.

24

17 апр.

21

24 апр.

18

2 мая

15

9 мая

12

1 0 мая

09

24 мая

06

1 июня

03

7 нюня

00

15 июня

97

23 июня

94

13

7 мирта

34

15 марта

31

22 марта

28

29 марта

25

6 апр.

22

14 апр.

19

20 апр.

10

28 апр.

13

б мая

10

13 мая

07

20 мая

04

28 мая

01

4 июня

98

12 июня

95

14

25 февр.

35

3 марта

32

11 марта

29

|9 марта

26

26 марта

23

2 апр.

20

10 апр.

17

17 апр.

14

25 апр.

11

2 мая

08

9 мая

05

17 мая

02

25 мая

99

31 мая

96

15

14 февр.

36

21 февр.

33

28 февр.

30

8 марта

27

15 марта

24

22 марта

21

30 марта

18

7 апр.

15

13 апр.

12

21 апр.

09

29 апр.

06

6 мая

03

13 мая

00

21 мая

97

1б

2 фенр.

37

10 февр.

34

18 февр.

31

25 февр.

78

4 марта

25

12 марта

22

9 марта

19

26 марта

16

3 апр.

13

10 апр.

10

18 апр.

IV

25 апр.

04

2 мая

11

10 май

98

17

23 янв.

38

31 янв.

35

7 февр.

32

14 февр.

29

22 феор.

26

1 марта

23

8 марта

20

16 марта

17

23 марта

14

31 марта

11

7 апр.

08

14 апр.

05

22 апр.

02

30 апр.

99

18

12 янв.

39

20 янв.

36

27 янв.

33

3 февр.

30

11 февр.

27

19 февр.

24

25 февр.

21

5 марта

18

13 марта

15

19 марта

12

7 марта

09

4 апр.

06

1 1 апр.

03

18 апр.

00

19

2 янв.

40

8 янв.

37

16 янв.

34

24 янв.

31

31 янв.

28

7 февр.

25

15 февр.

22

22 февр.

19

1 мирта

16

9 марта

13

6 марта

10

24 марта

07

11 марта

04

7 апр.

01

20

21 дек.

40

29 дек.

37

5 янв.

35

13 янв.

32

20 янв.

29

27 февр.

26

4 февр.

23

12 февр.

20

18 февр.

17

26 февр.

14

6 марта

11

12 марта

08

20 марта

05

28 марта

02

21

10 дек.

41

18 дек.

38

26 дек.

35

1янв.

33

9 янв.

30

17 янв.

27

24 янв.

24

31 янв.

21

8 февр.

18

1 5 февр.

15

23 февр.

12

2 марта

09

9 марта

06

17 марта

03

22

30 нояб. 

42 

7 дек.

39 

14 дек. 

36

22 дек.

33 

29 дек.

30 

6 янв. 

28 

13 янв. 

25

20 янв.

22 

28 янв. 

19 

5 фев. 

16 

11 февр.

13

19 февр. 

10 

27 февр.

07

5 марта 

04

23

19 нояб.

43

26 нояб.

40

3 дек.

37

11 дек.

34

19 дек.

31

25 дек.

28

2 янв.

26

10 янв.

23

17 янв.

20

24 янв.

17

1 февр.

14

8 февр.

11

16 февр.

08

23 февр.

05

24 

7 нояб.

44 

15 нояб.

41

23 нояб.

38 

30 нояб.

35

7 дек.

32 

15 дек.

29 

22 дек. 

26

30 дек.

23

6 янв. 

21 

13 янв. 

18 

21 янв.

15 

29 янв. 

12

4 фев. 

09 

12 фев. 

06

25

28 окт.

45

4 нояб.

42

12 нояб.

39

19 нояб.

36

26 нояб.

33

4 дек.

30

12 дек.

27

18 дек.

24

26 дек.

21

3 янв.

19

10 янв.

16

17 янв.

13

25 янв.

10

1 фев.

07

26

17 окт.

46

25 окт.

43

31 окт.

40

8 нояб.

37

16 нояб.

34

23 нояб.

31

30 нояб.

28

8 дек.

25

15 дек.

22

23 дек.

19

30 дек.

16

6 янв.

14

14 янв.

11

22 янв.

08

27

7 окт.

47

13 окт.

44

21 окт.

41

29 окт.

38

5 нояб.

35

12 нояб.

32

20 нояб.

29

27 нояб.

26

5 дек.

23

12 дек.

20

19 дек.

17

27 дек.

14

4 янв.

12

10 яни.

09

28

25 сен.

48

3 окт.

45

10 окт.

42

18 окт.

39

25 окт.

36

1 нояб.

33

9 нояб.

30

17 нояб.

27

23 нояб.

24

1 дек.

21

9 дек.

18

16 дек.

15

23 дек.

12

31 дек.

09

29

14 сен.

49

22 сен.

46

30 сен.

43

6 окт.

40

14 окт.

37

22 окт.

34

20 окт.

31

5 нояб.

28

13 нояб.

25

20 нояб.

22

28 нояб.

19

5 дек.

16

12 дек.

13

20 дек.

10

30

4 сен.

50

11 сен.

47

18 сен.

44

26 сен.

41

3 окт.

38

11 окт.

З5

18 окт.

32

25 окт.

29

2 нояб.

26

10 нояб.

23

16 нояб.

20

24 нояб.

17

2 дек.

14

9 дек.

11

31

24 авг.

51

31 авг.

46

7 сен.

45

15 сен.

42

23 сен.

39

29 сен.

36

7 окт.

33

15 окт.

30

22 окт.

27

29 окт.

24

6 нояб.

21

13 нояб.

18

21 нояб.

15

28 нояб.

12

32

12 авг.

52

20 авг.

49

28 авг.

46

4 сен.

43

11 сен.

40

19 сен.

37

26 сен.

34

4 окт.

31

1 1 окт.

28

18 окт.

25

26 окт.

22

3 нояб.

19

9 нояб.

16

17 нояб.

13

33

2 авг.

53

9 авг.

50

17 авг.

47

24 авг.

44

31 авг.

41

8 сен.

38

16 сен.

35

22 сен.

32

30 сен.

29

8 окт.

26

15 окт.

23

22 окт.

20

30 окт.

17

6 нояб.

14

34

22 июля

54

30 июля

51

5 авг.

48

13 авг.

45

21 авг.

42

28 авг.

39

41сен.

36

12 сен.

33

19 сен.

30

27 сен.

27

4 окт.

24

11 окт.

21

19 окт.

18

21 окт.

15

35

11 июля

55

18 июля

52

26 июля

49

2 авг.

46

10 авг.

43

17 авг.

40

24 авг.

37

1 сен.

34

9 сен.

31

15 сен.

28

23 сен.

25

1. окт.

22

8 окт.

19

15 окт.

16

36

30 июня

56

7 июля

53

15 июля

50

23 июля

47

29 июля

44

6 авг.

41

14 авг.

38

21 авг.

35

28 авг.

32

5 сен.

29

12 сен.

26

20 сен.

23

27 сен.

20

4 окт.

17

37

19 июня

57

27 июня

54

5  июля

51

11 июля

48

19 июля

45

27 июля

42

3 авг.

39

10 авг.

36

18 авг.

33

25 авг.

30

2 сен.

27

9 сен.

24

16 сен.

21

24 сен.

18

38

9 июня

58

16 июля

55

23 июня

52

1 июля

49

8  июля

46

16 толя

43

23 июля

40

30  июля

37

7 авг.

34

15 авг.

31

21 авг.

28

29 авг.

25

6 сен.

22

13 сен.

19

39

29 мая

59

5 июня

56

12 июня

53

20 июня

50

28 июня

47

4 июля

44

12 июля

41

20 июля

38

27 июля

35

3 авг.

32

11 авг.

29

18 авг.

26

26 авг.

23

2 сен.

20

40

17 мая

60

25 мая

57

2 июня

54

9 июня

51

16 июня

48

24 июня

45

1июля

42

9 июля

39

16 июля

36

23 июля

33

31 июля

З0

8 авг.

27

14 авг.

24

22 авг.

21

41

7 мая

61

14 мая

58

22 мая

55

29 мая

52

5 июня

49

13 нюня

46

21 июня

43

27 нюня

40

5 июля

37

13 июля

34

20 июля

31

27 июля

28

4 авг.

25

11 авг.

22

42

26 апр.

62

4 мая

59

10 мая

56

18 мая

53

26 мая

50

2 нюня

47

9 июня

44

17 июня

41

24 июня

38

2 июля

35

9  июля

32

16 июля

29

24 июля

26

1 авг.

23

43

15 апр.

63

22 апр.

60

30 апр.

57

7 мая

54

15 мая

51

22 мая

48

29 мая

45

6  июня

42

14 июня

39

20 июня

36

28 июня

33

6  июля

30

13 июля

24

20 июля

24

44

4 апр.

64

11 апр.

б1

19 апр.

58

27 апр.

55

3 мая

52

11 мая

49

19 мая

46

26 мая

43

2 июня

40

10 июня

37

17  июня

34

25 июня

31

2  июля

28

9 июля

25

45

24 марта

65

1 апр.

б2

8 апр.

59

15 апр.

56

23 апр.

53

30 апр.

50

16 апр.

47

15 мая

44

22 мая

41

30 мая

38

7 июня

35

13 июня

32

21 июня

29

29 нюня

26

46

13 марта

66

21 марта

63

28 марта

60

4 апр.

57

12 апр.

54

20 апр.

51

26 апр.

48

4 мая

45

12 мая

42

19 мая

39

26 мая

36

3  июня

33

10 июня

31

18 июня

27

47

3 марта

67

10 марта

64

17 марта

61

25 марта

58

2 апр.

55

8 апр .

52

16 апр.

49

24 агр.

46

1 мая

43

8 мая

40

16 мая

37

23 мая

34

31 мая

31

7 июня

28

48

20 февр.

68

27 февр.

65

7 марта

62

14 марта

59

21 марта

56

29 марта

53

5 апр.

50

13 апр.

47

20 апр.

44

27 апр.

41

5 мая

38

13 мая

35

19 мая

32

27 мая

29

49

9 февр.

69

16 февр.

66

24 февр.

63

3 марта

60

10 марта

57

18 марта

54

26.марта

51

1 апр.

48

9 апр.

45

17 апр.

42

24 япр.

39

1 мая

З6

9 мая

33

16 мая

30

a

b

c

b

c

b

c

b

c

b

c

b

c

b

c

b

c

b

c

b

c

b

c

b

c

b

c

b

c

    a) Десятки и единицы лет мусульманского летосчисления.
    c) То же современного европейского (христианского) летосчисления.
    b) Мусульманское новогодие по Юлианскому календарю.
 

 Таблица XXIV
(вторая половина)

Перевод дат с мусульманского летосчисления на современное европейское

Эра "от
рождества
христова"

6

7

 

7

8

 

8

9

 

9

10

 

10

11

 

11

12

 

12

 

13

 

14

 

15

 

16

 

17

 

18

 

19

Сот-
ни
лет

Эра 
Гиджры

0

 

1

 

2

 

3

 

4

 

5

 

6

 

7

 

8

 

9

 

10

 

11

 

12

 

13

50

29 янв.

70

6 февр.

67

13 февр.

64

20 февр.

61

28 февр.

58

7 марта

55

14 марта

52

22 марта

49

29 марта

46

6 апр.

43

13 апр.

40

20 апр.

37

28 апр.

34

6 мая 

31

51

18 янв.

71

26 янв.

68

2 февр

65

9 февр.

62

17 февр.

59

25 февр.

56

3 марта

53

11 марта

50

19 марта

47

25 марта

44

2 апр.

41

10 апр.

38

17 апр.

35

24 апр

32

52

8 янв.

72

14 янв.

69

22 янв.

66

30 янв.

63

6 февр.

60

13 февр.

57

21 февр.

54

28 февр.

51

7 марта

48

15 марта

45

22 марта

42

30 марта

39

6 апр.

36

13 апр.

33

53

27 дек.

72

4 янв.

70

11 янв.

67

19 янв.

64

26 янв.

61

2 февр.

58

10 февр.

55

18 февр.

52

24 февр.

49

4 марта

46

12 марта

44

18 марта

40

26 марта

37

3 апр.

34

54

16 дек.

73

24 дек.

70

1 янв.

68

7 янв.

65

15 янвю

62

23 янв.

59 

30 янв.

56

6 февр.

53

14 февр.

50

21 февр.

47

29 февр.

44

8 марта

41

15 марта

38

23 марта

35

55

6 дек.

74

13 дек.

71

20 дек.

68

28 дек.

65 

4 янв.

63

12 янв.

60

19 янв.

57 

26 янв.

54 

3 февр.

51

11 февр .

48 

17 февр.

45

25 февр.

42

5 марта

39

11 марта

З6

56

25 нояб.

75

2 дек.

72

9 дек.

69

17 дек.

66

25 дек.

63

31 дек.

60

8 янв.

58

16 янв.

55

23 янв.

52

30 янв.

49

7 февр.

46

14 февр.

43

22 февр.

40

1 марта

37

57

14 нояб.

76

21 нояб.

73

29 нояб.

70

7 дек.

67

13 дек.

64

21 дек.

61

29 дек.

58 

5 янв.

56

12 янв.

53

20 янв.

50 

27 янв.

47

4 февр.

44 

11 февр .

41

18 февр.

38

58

3 нояб.

77

11 нояб.

74

18 нояб.

71

25 нояб.

68

3 дек.

б5

10 дек.

б2

18 дек.

59

25 дек.

56

1 янв.

54

9 янв.

51

17 янв.

48

23 яна.

45

31 янв.

42

8 февр.

39

59

23 окт

78

31 окт.

75

7 нояб.

72

14 нояб.

69

22 няб.

66

30 нояб.

63

6 дек

60

14 дек.

57

22 дек.

54

29 дек.

51

5 янв.

49

13 янв.

46

20 янв.

43

28 янв.

40

60

13 окт.

79

19 окт.

76

27 окт.

73

4 нояб.

70

11 нояб.

67

18 нояб.

64

26 нояб.

61

3 дек.

58

11 дек.

55

18 дек.

52

25 дек.

49

2 янв.

47

10 янв.

44

16 янв.

41

61

1 окт.

80

9 окт.

77

16 окт.

74

24 окт.

71

31 окт.

68 

7 нояб.

65

15 нояб.

62

23 нояб.

59 

 29 нояб.

56 

7 дек.

5З

15 дек.

50

22 дек.

47

29 дек.

44

6 янв.

42

62

20 сен .

81

28 сен.

78

6 окт.

75

12 окт.

72

20 окт.

69

28 окт.

66

4 нояб

61

11 нояб.

60

19 нояб.

57

26 нояб

54

4 дек

51

11 дек.

48

18 дек

45

26 дек.

42

63

10 сен.

82

17 сен.

79

24 сен.

76

2 окт.

73

9 окт.

70

17 окт.

67

24 окт.

64

31 окт.

61

8 нояб.

58

16 нояб.

55

22 нояб.

52

30 нояб.

49

8 дек. 

46

15 дек.

43

64

30 авг.

83

6 сен.

80

13 сен.

77

21 сен.

74

29 сен.

71

5 окт.

68

13 окт.

65

21 окт.

62

28 окт.

59

4 нояб.

56

12 нояб.

53

19 нояб.

50

27 нояб

47

4 дек.

44

65

18 адг

84

26 авг.

81

3 сен.

78

10 сен.

75

17 сен.

72

25 сен.

69

2 окт.

66

10 окт.

63

17 окт.

60

24 окт.

57

1 нояб.

54

9 нояб. 

51

15 нояб.

48

23 нояб.

45

66

8 авг.

85

15 авг.

82

23 авг.

79

30 авг.

76

6 сен.

73

14 сен.

70

22 сен.

67

28 сен.

64

6 окт.

61

14 окт.

58

21 окт.

55

28 окт.

52

5 нояб.

49

12 нояб.

46

67

28 июля

86

5 авг.

83

12 авг.

80

19 авг.

77

27 авг.

74

4 сен.

71

10 сен.

68

18 сен.

б5

26 сен.

62

3 окт.

59

10 окт.

56

18 окт.

53

25 окт.

50

2 нояб.

47

68

18 июля

87

24 июля

84

1 авг.

81

9 авг.

78

16 авг.

75

23 авг.

72

31 авг.

69

7 сен.

66

15 сен.

63

22 сен.

60

29 сен.

57

7 окт.

54

15 окт.

51

21 окт.

48

69

6 июля

88

14 июля

85

21 июля

82

29 июля

79

5 авг.

76

12 авг.

73

20 авг.

70

28 авг.

67

3 сен.

64

11 сен.

61

19 сен.

58

26 сен.

55

3 окт.

52

11 окт. 

49

70

25 июня

89

3 июля

86

11 июля

83

17 июля

80

25 июля

77

2 авг.

74

9 авг.

71

16 авг.

б8

24 авг.

65

31 авг.

62

8 сен.

59

15 сен.

56

22 сен.

53

30 сен.

50

71

15 июня

90

22 июня

87

29 июня

84

7 июля

81

14 июля

78

22 июля

75

29 июля

72

5 авг.

69

13 авг.

66

21 авг.

63

27 авг.

60

4 сен.

57

12 сен.

54

19 сен.

51

72

4 июня

91

11 июня

88

18 июня

85

26 июня

82

4 июля

79

11 июля

76 

18 июля

73

26 июля

70

2 авг.

67

9 авг.

64

17 авг.

61

24 авг.

58

1 сен.

55

8 сен.

52

73

23 мая

92

31 мая

89

8 июня

86

15 июня

83

22 июня

80

31 июня

77

7 июля

74

15 июля

71

22 июля

68

29 июля

65

6 авг.

62

14 авг.

59

20 авг.

56

28 авг.

53

74

13 мая

93

20 мая

90

28 мая

87

4 июня

84

1 1 июня

81

19 июня

78

27 июня

75

3 июля

72

11 июля

69

19 июля

66

26 июля

63

2 авг.

60

10 авг.

57

17 авг.

54

75

2 мая

94 

10 мая

91

16 мая

88

24 мая

85

1 июня

82

8 июня

79

15 июня

76

23 июня

73

30 июня

70

8 июля

67

15 июля

64

22 июля

61

30 июня

58

6 авг.

55

76

21 апр.

95

28 апр.

92

6 мая

89

13 мая

86

21 мая

83

28 мая

80

4 июня

77

12 июня

74

20 июня

71

26 июня

68

4 июля

65

12 июня

62

19 июля

59

26 июля

56

77

10 апр.

96

18 апр.

93

25 апр.

90

3 мая

87

10 мая

84

17 мая

81

25 мая

78

2 июня

75

8 июня

72

16 июня

69

24 июня

66

1 июля

63

8 июля

60

16 июля

57

78

30 марта

97 

7 апр. 

94

15 апр.

91

21 апр.

88

29 лир.

85

7 мая

82

14 мая

79

21 мая

76

29 мая

73

5 нюня

70

13 июня

67

20 июня

64

27 нюня

61

5 июля

58

79

20 марта

98

27 марта

95

3 апр.

92

11 апр.

89

18 апр.

86

26 апр.

83

3 мая

80

10 мая

77

18 мая

74

26 мая

71

1 нюня

68

9 июня

65

17 июня

62

24 июня

59

80

9 марта

99

16 марта

96

23 марта

93

31 марта

90

8 апр.

87

14 апр.

84

22 апр.

81

30 апр.

78

 7 мая

75

14 мая

72

22 мая

69

29 мая

66

6 июня

63

13 июня

60

81

26 февр.

00

5 марта

97

12 марта

94

20 марта

91

27 марта

88

4 апр.

85

11 апр.

82

19 апр.

79

26 апр.

76

3 мая

73

11 мая

70

19 мая

67

25 мая

64

3 июня

61

82

15 февр.

01

22 февр.

98

2 марта

95

9 марта

92

16 марта

89

24 марта

86

1 апр.

83

7 апр.

80

10 апр.

77

23 апр.

74

30 апр.

71

7 мая

68 

15 мая

65

22 мая

62

83

4 февр.

02

12 февр.

99

19 февр.

96

26 февр

93

6 марта

90

13 марта

87

20 марта

84

28 марта

81

4 апр.

78

12 апр

75

19 апр.

72

26 апр.

69

4 мая

66

12 мая

63

84

24 янв.

03

1 февр.

00

8 февр.

97

15 февр.

94

23 февр.

91

2 марта

88

9 марта

85

17 марта

82

25 марта

79

31 марта

76

8 апр.

73

16 апр.

70

23 апр. ;

67

30 апр.

64

85

14 янв.

04

20 янв.

01

28 янв.

98

5 февр.

95

12 февр.

92

19 февр.

89

27 февр.

86

6 марта

83

13 марта

80

21 марта

77

28 марта

74

5 апр.

71

12 апр.

68

19 апр.

65

86

2 янв.

05

10 янв.

02

17 янв.

99

25 янв.

96

1 февр.

93

8 февр.

90

16 февр.

87

24 февр.

84

2 марта

81

10 марта

78

18 марта

75

24 марта

72

1апр.

69

9 апр.

66

87

23 дек.

05

30 дек.

02

7 янв.

00

14 янв.

97

21 янв.

94

29 янв.

91

6 февр.

88

12>свр.

85

20 февр.

82

28 февр.

19

6 марта

76

14 марта

73

22 марта

70

29 марта

67

88

12 дек.

06

20 дек.

03

26 дек.

00

3 янв.

98

11 янв.

95

18 янв.

92

25 янв.

89

2 февр.

86

9 февр.

83

17 февр.

80

24 февр.

77

3 марта

74

11 марта

71

18 марта

68

89

1 дек.

07

8 дек.

04

16 дек..

01

23 дек.

98

31 дек.

95

7 янв.

93

14 янв.

90

22 янв.

87

30 янв.

84

5 февр.

81

13 февр.

78

21февр.

75

28 февр.

72

7 марта

69

90

20 нояб.

08

27 нояб.

05

5 дек.

02

13 дек.

99

19 дек.

96

27 дек.

93

4 янв.

91

11 янв.

88

18 янв.

85

26 янв.

82

2 февр.

79

10 февр.

76

17 февр.

73

24 февр.

70

91

9 нояб.

09

17 нояб.

06

24 нояб.

03

1 дек.

00

9 дек. 

97

16 дек.

94

24 дек.

91

31 дек.

88

7 янв.

86

15 янв.

83

23 янв.

80

29 янв.

77

6 февр.

74

14 февр.

71

92

29 окт.

10

6 нояб.

07

13 нояб.

04

20 нояб.

01

28 нояб.

98

6 дек.

95

12 дек.

92

20 дек.

89

28 дек.

86

4 янв.

84

11 янв.

81

19 янв.

78

26 янв.

75

3 февр.

72

93 

19 окт.

11

25 окт.

08

2 нояб.

05

10 нояб.

02

17 нояб.

99

24 нояб.

96

2 дек.

93

9 дек.

90

17 дек.

87

24 дек.

84

31 дек.

81

 8 янв.

79

16 янв.

76

22 янв.

73

94

7 окт.

12

15 окт.

09

22 окт.

06

30 окт.

03

6 нояб.

00

13 нояб.

97

21 нояб.

94

29 нояб.

91

5 дек.

88

13 дек.

85

21 дек.

82

28 дек.

79

4 янв.

77

12 янв.

74

95

26 сен.

13

4 окт.

10

12 окт.

07

18 окт.

04

26 окт.

01

3 нояб.

98

10 нояб.

95

17 нояб.

92

25 нояб.

89

2 дек.

86

10 дек.

83

17 дек.

80

24 дек.

77

1 янв.

75

96

16 сен.

14

23 сен.

11

30 сен.

08

8 окт.

05

15 окт.

02

23 окт.

99

30 окт.

96

6 нояб.

93

14 нояб.

90

22 нояб.

87

28 нояб.

84

6 дек.

81

14 дек.

78

21 дек.

75

97 

5 сен.

15

12 сен.

12

20 сен.

09

27 сен.

06

5 окт.

03

12 окт. 

00

19 окт.

97

27 окт.

94

4 нояб. 

91

10 нояб. 

88

18 нояб.

85

26 нояб.

82

3 дек.

79

10 дек.

76

98

25 авг.

16

1 сен.

13

9 сен.

10

17 сен.

07

23 сен.

04

1 окт.

01

9 окт.

98

16 окт.

95

23 окт.

92

31 окт.

89

7 нояб.

86

15 нояб.

83

22 нояб.

80

29 нояб.

77

99

14 авг.

17

22 авг.

14

29 авг.

11

5 сен.

08

13 сен.

05

20 сен.

02

28 сен.

99

5 окт.

96

12 окт.

93

20 окт.

90

27 окт.

87

3 нояб.

84

11 нояб.

81

19 нонб.

78

a

b

c

b

с

b

c

b

c

b

c 

b

c

b

c

b

c

b

c

b

c

b

c

b

c

b

c

b

c

-82-

обычно указывают, что событие произошло "в таком-то году такой-то (по счету) Луны (или месяца)". Иногда счет велся еще по четырем временам года или сезонам (весна, лето, осень и зима), при чем каждый сезон подразделялся на три месяца (луны). Отсюда -- такие календарные даты: первая летняя луна (месяц), средняя летняя луна (месяц), первая зимняя луна и т. д. Год начинался весной, при чем первый весенний месяц соответствовал нашему январю или февралю. Месяц делился на две половины, из которых первая называлась новой, а вторая -- старой или ветхой. Таким образом, мы можем, например, встретить в документе такое указание: "осеннего первого месяца (луны) в четвертый день ветха", т. е. речь идет о 4-м числе второй половины первого осеннего месяца (седьмого месяца от начала года).
        В основу тюрко-монгольского летосчисления был положен также особый циклический счет. Вначале монголы исходили из периода в 12 лет. Каждый год в пределах двенадцатилетнего цикла назывался именем определенного животного. Первый год носил название мыши или крысы; второй -- коровы, тельца или быка; третий -- барса или тигра; четвертый -- зайца; пятый -- дракона или крокодила; шестой -- змеи; седьмой -- лошади (коня); восьмой -- овцы или барана; девятый -- обезьяны; десятый -- курицы; одиннадцатый -- собаки (пса); двенадцатый -- свиньи.
        Впоследствии, под влиянием китайцев, монголы удлиннили первоначальный двенадцатилетний цикл до шестидесятилетнего. Последний строился путем комбинации названий двенадцати животных и пяти стихий (дерево, огонь, земля, железо и вода). При этом наименования животных сменялись в пределах цикла ежегодно, наименования стихий применялись к каждым двум годам, идущим подряд. При такой системе сочетание названий определенного животного и определенной стихии встречалось только один раз в 60 лет. Например, в каждом шестидесятилетнем цикле был только один год воды и лошади, один год огня и обезьяны, один год железа и курицы и т. д.
        Для того, чтобы отличить друг от друга два соседних года, носящих, как указано, наименование одной и той же стихии, к первому присоединялось иногда указание на мужской род, ко второму -- на женский. Например: мужской род, год дерева и мыши; женский род, год дерева и коровы.
        Вместо названий стихий иногда употреблялись названия пяти цветов. При этом каждой стихии соответствовал определенный цвет: дереву -- голубой или синий, огню -- красный, земле -- желтый, железу -- белый, воде -- черный. В том случае, когда стихия употреблялась в сочетании с годом мужского рода, заменяющий ее цвет выступал в своей обычной форме (голубой, красный, желтый и пр.). В применении к году женского рода названия тех же цветов встречаются в уменьшительной форме: вместо "голубой" --"голубоватый", вместо "красный" -- "красноватый" и т. д.
        Таким образом, отдельные годы в пределах тюрко-монгольского шестидесятилетнего цикла могут быть обозначены следующим

-83-

образом: "год дерева и мыши" или "год синей мыши"; "год воды и курицы" или "год черноватой курицы" и т. д. 1).
        Следует тадже отметить, что каждый год шестидесятилетнего цикла, помимо своего наименования определенным животным и стихией, носит еще особое название. Так четвертый год (огня и зайца) именуется "совершенным", двенадцатый, (дерева и свиньи) --"исполненным жизни" и т. д.
        При циклической системе времясчисления должна быть установлена какая-то исходная точка (эра), от которой ведется счет циклов. Монгольская эра заимствована из Тибета. Шестидесятилетние монгольские циклы считаются от 1027 г., который и является начальным годом тюрко-монгольской системы летосчисления ("рабчжуном"), занимая четвертое порядковое место в первом цикле (см. таблицу XXV). Поскольку 1027 г. по тюркомонгольской номенклатуре был годом огня и зайца, постольку все дальнейшие хронологические даты приводятся тоже в циклах (кругах) огня и зайца. Когда например, говорят: "второй цикл (круг) огня и зайца"; то значит, что речь идет о втором шестидесятилетнем периоде по тюрко-монгольской эре, т. е. от 1027 г. (рабчжуна), который носил название огня и зайца и был четвертым по счету в исходном цикле.
        В целях точной датировки, монгольские хронологические данные обычно содержат указания: 1) на название года, соответственно занимаемому им порядковому месту в пределах текущего шестидесятилетнего цикла; 2) на порядковый номер цикла (круга) огня и зайца, т. е. того незаконченного шестидесятилетнего периода 2), в котором находится интересующий нас год. Например: год воды и барса в одиннадцатом кругу огня и зайца. Или: "год беловатой змеи в двенадцатом кругу огня и зайца.
        Ниже приводится таблица XXV, в которой дано соответствие тюрко-монгольской и современной европейской систем летосчисления. Перевод дат с монгольской эры на современную производится следующим образом. В левой крайней вертикальной графе таблицы мы находим указанное нам наименование года в пределах монгольского шестидесятилетнего цикла. Проводим от него вправо горизонтальную линию вплоть до той вертикальной графы, где находится дата, являющаяся монгольской эрой, т. е. 1027 г. Это первая по счету графа, содержащая даты. От этой графы по той же горизонтали отсчитываем еще столько десятилетий, сколько нам указано, циклов огня и зайца, и находим соответствующую дату современной зры.
        Перевод дат с тюрко-монгольского летосчисления на современное производится также по особой формуле, при чем в этом случае таблица играет лишь второстепенную вспомогательную роль. Формула перевода такова:
        X = 1027 + N + C - 4.
        ___________
        1) Отдельные дни монгольского календаря также носили комбинированные названия животных и стихий (цветов).
        2) Считая начальным тот цикл, где 4-е место занимал 1027 г. - год огня и зайца.

 Таблица XXV
(первая половина)

Перевод дат с тюрко-монгольского летосчисления на современное европейское

Наименования годов монгольского 
шестидесятилетнего цикла

Даты современного европейского летосчисления

1. М. Р. дерева (голубой, синий) мыши

 

1084

1144

1204

1264

1324

1384

1444

1504

1564

1624

1684

1744

1804

1864

1924

2. Ж. Р. дерева (голубоватый, синеватый) коровы (тельца, быка)

 

1085

1145

1205

1265

1325

1385

1445

1505

1565

1625

1685

1745

1805

1865

1925

3. М. Р. огня (красный) барса (тигра)

 

1086

1146

1206

1266

1326

1386

1446

1506

1566

1626

1686

1746

1806

1866

1926

4. Ж. Р. огня (красноватый) зайца

1027

1087

1147

1207

1267

1327

1387

1447

1507

1567

1627

1687

1747

1807

1867

1927

5. М. Р. земли (желтый) дракона (крокодила)

1028

1088

1148

1208

1268

1328

1388

1448

1508

1568

1628

1688

1748

1808

1868

1928

6. Ж. Р. земли (желтоватый) змеи

1029

1089

1149

1209

1269

1329

1389

1449

1509

1569

1629

1689

1749

1809

1869

1929

7. М. Р. железа (белый) лошади (коня)

1030

1090

1150

1210

1270

1330

1390

1450

1510

1570

1630

1690

1750

1810

1870

1930

8. Ж. Р. железа (беловатый) овцы (барана, овна)

1031

1091

1151

1211

1271

1331

1391

1451

1511

1571

1631

1691

1751

1811

1871

1931

9. М. Р. воды (черный)  обезьяны

1032

1092

1152

1212

1272

1332

1392

1452

1512

1572

1632

1692

1752

1812

1872

1932

10. Ж. Р. воды (черноватый) курица

1033

1093

1153

1213

1273

1333

1393

1453

1513

1573

1633

1693

1753

1813

1873

1933

11. М. Р. дерева (голубой, синий) собаки

1034

1094

1154

1214

1274

1334

1394

1454

1514

1574

1634

1694

1754

1814

1874

1934

12. Ж. Р. дерева (голубоватый, синеватый) свиньи

1035

1095

1155

1215

1275

1335

1395

1455

1515

1575

1635

1695

1755

1815

1875

1935

13. М. Р. огня (красный)  мыши

1036

1096

1156

1216

1276

1336

1396

1456

1516

1576

1636

1696

1756

1816

1876

1936

14. Ж. Р. огня (красноватый)  коровы (тельца, быка)

1037

1097

1157

1217

1277

1337

1397

1457

1517

1577

1637

1697

1757

1817

1877

1937

15. М. Р. земли (желтый) барса (тигра)

1038

1098

1158

1218

1278

1338

1398

1458

1518

1578

1638

1698

1758

1818

1878

1938

16. Ж. Р. земли (желтоватый)  зайца

1039

1099

1159

1219

1279

1339

1399

1459

1519

1579

1639

1699

1759

1819

1879

1939

17. М. Р. железа (белый) дракона (крокодила)

1040

1100

1160

1220

1280

1340

1400

1460

1520

1580

1640

1700

1760

1820

1880

1940

18. Ж. Р. железа (беловатый)  змеи

1041

1101

1161

1221

1281

1341

1401

1461

1521

1581

1641

1701

1761

1821

1881

1941

19. М. Р. воды (черный)  лошади (коня)

1042

1102

1162

1222

1282

1342

1402

1462

1522

1582

1642

1702

1762

1822

1882

1942

20. Ж. Р. воды (черноватый)   овцы (барана, овна)

1043

1103

1163

1223

1283

1343

1403

1463

1523

1583

1643

1703

1763

1823

1883

1943

21. М. Р.  дерева (голубой, синий) обезьяны

1044

1104

1164

1224

1284

1344

1404

1464

1524

1584

1644

1704

1764

1824

1884

1944

22. Ж. Р. дерева (голубоватый, синеватый)  курицы

1045

1105

1165

1225

1285

1345

1405

1465

1525

1585

1645

1705

1765

1825

1885

1945

23. М. Р. огня (красный) собаки

1046

1106

1166

1226

1286

1346

1406

1466

1526

1586

1646

1706

1766

1826

1886

1946

24. Ж. Р.  огня (красноватый) свиньи

1047

1107

1167

1227

1287

1347

1407

1467

1527

1587

1647

1707

1767

1827

1887

1947

25. М. Р. земли (желтый)  мыши 

1048

1108

1168

1228

1288

1348

1408

1468

1528

1588

1648

1708

1768

1828

1888

1948

26. Ж. Р. земли (желтоватый)  коровы (тельца, быка)

1049

1109

1169

1229

1289

1349

1409

1469

1529

1589

1649

1709

1769

1829

1889

1949

27. М. Р. железа (белый) барса (тигра)

1050

1110

1170

1230

1290

1350

1410

1470

1530

1590

1650

1710

1770

1830

1890

1950

28. Ж. Р. железа (беловатый) ; зайца

1051

1111

1171

1231

1291

1351

1411

1471

1531

1591

1651

1711

1771

1831

1891

1951

29. М. Р. воды (черный)  дракона (крокодила)

1052

1112

1172

1232

1292

1352

1412

1472

1532

1592

1652

1712

1772

1832

1892

1952

30. Ж. Р.  воды (черноватый)  змеи

1053

1113

1173

1233

1293

1353

1413

1473

1533

1593

1653

1713

1773

1833

1893

1953

 Таблица XXV
(вторая половина)

Перевод дат с тюрко-монгольского летосчисления на современное европейское

Наименования годов монгольского 
шестидесятилетнего цикла

Даты современного европейского летосчисления

31. М. Р. дерева (голубой, синий) лошади (коня)

1054

1114

1174

1234

1294

1354

1414

1474

1534

1594

1654

1714

1774

1834

1894

1954

32. Ж. Р. дерева (голубоватый, синеватый)  овцы (барана, овна)

1055

1115

1175

1235

1295

1355

1415

1475

1535

1595

1655

1715

1775

1835

1895

1955

33. М. Р. огня (красный) обезьяны

1056

1116

1176

1236

1296

1356

1416

1476

1536

1596

1656

1716

1776

1836

1896

1956

34. Ж. Р. огня (красноватый) курицы

1057

1117

1177

1237

1297

1357

1417

1477

1537

1597

1657

1717

1777

1837

1897

1957

35. М. Р. земли (желтый) собаки

1058

1118

1178

1238

1298

1358

1418

1478

1538

1598

1658

1718

1778

1838

1898

1958

36. Ж. Р. земли (желтоватый) свиньи

1059

1119

1179

1239

1299

1359

1419

1479

1539

1599

1659

1719

1779

1839

1899

1959

37. М. Р. железа (белый) мыши

1060

1120

1180

1240

1300

1360

1420

1480

1540

1600

1660

1720

1780

1840

1900

1960

38. Ж. Р. железа (беловатый) (тельца, быка)

1061

1121

1181

1241

1301

1361

1421

1481

1541

1601

1661

1721

1781

1841

1901

1961

39. М. Р. воды (черный) барса (тигра)

1062

1122

1182

1242

1302

1362

1422

1482

1542

1602

1662

1722

1782

1842

1902

1962

40. Ж. Р. воды (черноватый) зайца

1063

1123

1183

1243

1303

1363

1423

1483

1543

1603

1663

1723

1783

1843

1903

1963

41. М. Р. дерева (голубой, синий) дракона (крокодила)

1064

1124

1184

1244

1304

1364

1424

1484

1544

1604

1664

1724

1784

1844

1904

1964

42. Ж. Р. дерева (голубоватый, синеватый) змеи

1065

1125

1185

1245

1305

1365

1425

1485

1545

1605

1665

1725

1785

1845

1905

1965

43. М. Р. огня (красный)  лошади (коня)

1066

1126

1186

1246

1306

1366

1426

1486

1546

1606

1666

1726

1786

1846

1906

1966

44. Ж. Р. огня (красноватый)  овцы (барана, овна)

1067

1127

1187

1247

1307

1367

1427

1487

1547

1607

1667

1727

1787

1847

1907

1967

45. М. Р. земли (желтый) обезьяны 

1068

1128

1188

1248

1308

1368

1428

1488

1548

1608

1668

1728

1788

1848

1908

1968

46. Ж. Р. земли (желтоватый) курицы

1069

1129

1189

1249

1309

1369

1429

1489

1549

1609

1669

1729

1789

1849

1909

1969

47. М. Р. железа (белый) собаки

1070

1130

1190

1250

1310

1370

1430

1490

1550

1610

1670

1730

1790

1850

1910

1970

48. Ж. Р. железа (беловатый) свиньи

1071

1131

1191

1251

1311

1371

1431

1491

1551

1611

1671

1731

1791

1851

1911

1971

49. М. Р. воды (черный) мыши

1072

1132

1192

1252

1312

1372

1432

1492

1552

1612

1672

1732

1792

1852

1912

1972

50. Ж. Р. воды (черноватый) коровы (тельца, быка)

1073

1133

1193

1253

1313

1373

1433

1493

1553

1613

1673

1733

1793

1853

1913

1973

51. М. Р. дерева (голубой, синий) барса (тигра)

1074

1134

1194

1254

1314

1374

1434

1494

1554

1614

1674

1734

1794

1854

1914

1974

52. Ж. Р. дерева (голубоватый, синеватый) зайца

1075

1135

1195

1255

1315

1375

1435

1495

1555

1615

1675

1735

1795

1855

1915

1975

53. М. Р. огня (красный) дракона (крокодила)

1076

1136

1196

1256

1316

1376

1436

1496

1556

1616

1676

1736

1796

1856

1916

1976

54. Ж. Р. огня (красноватый) змеи

1077

1137

1197

1257

1317

1377

1437

1497

1557

1617

1677

1737

1797

1857

1917

1977

55. М. Р. земли (желтый)  лошади (коня) 

1078

1138

1198

1258

1318

1378

1438

1498

1558

1618

1678

1738

1798

1858

1918

1978

56. Ж. Р. земли (желтоватый) овцы (барана, овна)

1079

1139

1199

1259

1319

1379

1439

1499

1559

1619

1679

1739

1799

1859

1919

1979

57. М. Р. железа (белый) обезьяны

1080

1140

1200

1260

1320

1380

1440

1500

1560

1620

1680

1740

1800

1860

1920

1980

58. Ж. Р. железа (беловатый) курицы

1081

1141

1201

1261

1321

1381

1441

1501

1561

1621

1681

1741

1801

1861

1921

1981

59. М. Р. воды (черный) собаки

1082

1142

1202

1262

1322

1382

1442

1502

1562

1622

1682

1742

1802

1862

1922

1982

60. Ж. Р. воды (черноватый) свиньи

1083

1143

1203

1263

1323

1383

1443

1503

1563

1623

1683

1743

1803

1863

1923

1983

-84-

        Под X подразумевается искомая дата современной европейской (христианской) эры. Буквой N обозначено то порядковое место, какое занимает название данного нам монгольского года внутри шестидесятилетнего цикла. C -- количество лет в пределах полных (закончившихся до переводимой даты) кругах огня и зайца (т. е. шестидесятилетних циклах, отсчитываемых от того, в котором под четвертым номером помещен 1027 г., известный под именем огня и зайца).
        Выяснить значение формулы не представляется трудным. Монгольское летосчисление началось на 1027 лет после нашего (христианского). Следовательно, естественно, что при переводе дат с монгольской эры на нашу прежде всего надо учесть это число 1027 в качестве основного слагаемого. Его надо увеличить далее на количество лет, содержащееся в пределах тех циклов огня и зайца, которые закончились полностью до наступления монгольской даты, подлежащей переводу. Последний текущий цикл мы, конечно, должны брать в качестве слагаемого не целиком. Нам необходимо отсчитать в нем только то количество лет, на которое указывает нам порядковый номер, занимаемый в цикле названием интересующей нас монгольской даты. Легко убедиться, что сумма (1027 + N + С) допускает ошибку в 4 единицы при переводе монгольской даты на нашу эру. Дело в том, что 1027 г. (год огня и зайца), как это видно из таблицы, занимает четвертое место в цикле. Значит, при подсчете полных циклов (C) от 1027 г. в первом кругу иадо было считать не 60, а только 56 лет. Путем вычитания 4 мы исправляем эту неточность.
        Приведем конкретный пример применения формулы. Пусть нам дан год красного барса в одиннадцатом кругу огня и зайца.
        Год красного барса занимает третье место в цикле (см. таблицу). Следовательно, N = 3. Полных циклов огня и зайца прошло 10. Поэтому C = 10 х 60 = 600. Итак X = 1027 + 600 + 3 - 4 = 1626 г.
        Из всего вышеизложенного совершенно ясно, что перевод монгольских хронологических данных на нашу эру возможен только в том случае, если эти данные содержат указания на какой-то круг огня и зайца. При отсутствии подобной ссылки, мы лишены возможности дать точный перевод. В самом деле, если в источнике назван, например, год желтого дракона, то трудно сказать, какому именно году европейской (христианской) эры он соответствует. Ведь это название повторяется через каждые 60 лет. Но если дата уточнена дополнительным упоминанием какого-то определенного (скажем, 5-го) круга огня и зайца, то в этом случае вступает в силу выведенная выше формула и перевод на наше летосчисление производится без всяких затруднений.
        Предельной же точности этот перевод может достигнуть лишь в том случае, когда источники дают не только название года по циклической системе и круг огня и зайца, но также называют число и месяц монгольского календаря. Независимо от того, приведен ли общий порядковый номер месяца внутри года (первая луна, вторая луна и т. д.), или указано место, занимаемое им

-85-

в пределах определенного сезона (первая летняя луна, вторая зимняя и т. д.), при всех случаях надо иметь в ввиду, что начало каждого монгольского месяца совпадало с новолунием. Первый месяц нового года начинался с момента январского новолуния (если оно было во второй половине) или с февральского (в первой половине). При счете временами года следует учитывать, как это уже и было отмечено выше, что первым сезонам, падающим на январь по Юлианскому календарю, была весна, вторым -- лето, затем -- осень и зима. Длительность каждого сезона была равна трем месяцам. В случае деления месяца на две половины (новую и старую или ветхую), надо исходить из средней продолжительности лунного месяца = около 29,5 суток. В целях облегчения перевода дат, можно несколько округлить это число и довести его до 30.
        Повторяю, что удобство тюрко-монгольского календаря по сравнению, например, с мусульманским, заключается в том, что он устанавливает определенную связь между солнечным годом и лунным месяцем. Поэтому исключена возможность блуждания монгольского новогодия, подобно мусульманскому, по всем датам Юлианского календаря.
        Итак, совершенно очевидно, что при точном переводе дат с монгольской системы летосчисления на нашу необходимо прежде всего уметь, устанавливать момент новолуния для каждого месяца любого Юлианского года, т. к. время новолуния определяет (в датах Юлианского календаря) начало соответственного монгольского месяца. Ниже приводится таблица XXVI, с помощью которой легко разрешается эта предварительная задача. В ее основу (как и в основу монгольской хронологии) положен девятнадцатилетний лунный цикл. Ведь мы уже хорошо знаем, что через каждые 19 лет фазы луны приходятся на одни и те же числа солнечного года. Построение этой таблицы несколько отлично от таблицы, при посредстве которой находятся круги луны. Там на основе древне-русской хронологии 19-летний цикл поставлен в связь с византийской эрой (от "сотворения мира").
        Таблица, помещаемая ниже, исходит из современной системы летосчисления (от "рождества христова"). В левой вертикальной графе помещены порядковые номера девятнадцатилетнего цикла. Против каждого номера указаны числа новолуний для каждого из двенадцати месяцев тех лет, которые занимают данное порядковое место в пределах лунного цикла. Циклический счет строится начиная с 1 года нашей эры. Следовательно, узнав остаток от деления интересующей нас даты на 19 и установив таким образом ее номер в цикле, находим затем по таблице все двенадцать дат новолуний даиного года. В целях уточнения таблицы 1) в эти даты новолуний следует внести следующие поправки:
        ___________
        1) Соответствие дат новолуний раз в 19 лет не учитывает некоторого расхождения в часах и минутах. С течением времени это расхождение становится ощутительным и выражается уже в сутках. Даже при пользовании таблицей поправок надо учитывать возможность расхождения в пределах 1--2 дней.

-86-

Для

IV--VI

столетий

уменьшить

дату

на

1

"

VII--IX

"

"

"

"

2

"

X--XII

"

"

"

"

3

"

XIII--XV

"

"

"

"

4

"

XVI--XVIII

"

"

"

"

5

"

XIX--XX

"

"

"

"

6


        Тюрко-монгольский счет встречается в очень интересных источниках периода феодальной раздробленности -- ярлыках (грамотах) ханов Золотой Орды русским князьям и митрополитам XIII--XIV в.в., предоставляющих ряд привилегий церковным феодалам. Эти ярлыки дошли до нас в русском переводе.
        Так, например, в грамоте ханши Тайдулы в. кн. Семену Ивановичу имеется дата: "свиного лета осмого месяца в пятый ветха". Год свиньи в княжение Семена Ивановича Гордого (1341--1353) имел место только один раз 1). По современной эре это -- 1347 г. В лунном цикле 1347 г. занимает 17 место (1347:19 = 70 и 17 в остатке). Январское новолуние для года с порядковым номером 17 приходится на 16 января, а с поправкой на 4 для XIV в. -- на 12 января 2). Следовательно, монгольское новогодие падает уже иа февраль, именно (учитывая поправку) -- на 10 число 2). Восьмой месяц начинается 5 сентября 2), а вторая (ветхая) его половина через 15 дней, т. е. 20 сентября, 5 день второй (ветхой), половины -- 24 сентября 1347 г.
        Второй пример: грамота Тайдулы в подтверждение ярлыка Джанибека митрополиту Алексею от "ентя года, арама месяца во второй ветха". "Ентя года" значит: в год лошади, которым за время митрополита Алексея и хана Джанибека был только 1354 г. Юлианского календаря (см. таблицу XXV). Месяц арам (испорченное слово: мухаррам) = первый (новогодний) месяц 3). По таблице XXVI (с соответственными поправками для XIV в.) в 1354 г. январское новолуние, совпадающее с монгольским новогоднем, было 24 января. Ветхая (вторая) половина первого месяца (арама или по мусульманскому календарю -- мухаррама) считается с 8 февраля (т. е. через 15 дней), а 2-й день этой половины (придется, следовательно, на 9 февраля.
         § 6. Взаимоотношение мусульманской и тюрко-монгольской систем летосчисления. Иногда в источниках мы встречаем параллельно две системы датировки: и мусульманскую и монгольскую. Такой комбинированный счет облегчает взаимный контроль и уточнение хронологических дат. Так, например, если в документе указано, что он выдан в год курицы (по монгольскому циклическому счету), соответствующий 634 г. эры гиджры, то мы прежде всего производим перевод с эры гиджры на современное летосчисление. 634 мусульманский год падает на период с 4 сентября 1236 г. по 24 августа 1237 г. н. э. (см. таблицу XXIV). Годом курицы в монгольском цикле был 1237 г. (см. таблицу XXV). Поэтому дата уточняется. Период с 4 сентября 1236 г. по 24 августа
        ___________
        1) См. таблицу XXV.
        2) См. таблицу XXVI.
        3) Мусульманское название в применении к монгольскому календарю.

-87-

1237 г. сокращается до следующих пределов: 27 января (монгольское новогодие: см. таблицу XXVI с поправкой для XIII в.) -- 24 августа 1237 г.

 Таблица XXVI

Новолуния

Порядковый
N года в
лунном цикле

Месяцы Юлианского года

Январь

Февраль

Март

Апрель

Май

Июнь

Июль

Август

Сентябрь

Октябрь

Ноябрь

Декабрь

1

13

11

13

11

11

9

9

7

6

6

4

4

2

2

1

2

1 и 3

30

28

28

26

25

24

23

22

3

21

20

21

20

19

18

17

16

14

14

12

12

4

10

9

9

8

8

6

6

4

3

2

1 и 30

30

5

28

27

28

27

26

25

24

23

22

21

20

19

6

18

16

18

16

16

14

14

12

11

10

9

8

7

7

6

7

6

5

4

3

2 и 31

30

29

28

27

8

26

24

25

24

23

22

21

20

18

18

16

16

9

14

13

14

13

12

11

10

9

8

7

6

5

10

4

2

4

2

2 и31

30

29

28

26

26

24

24

11

23

21

23

21

21

19

19

17

16

15

14

13

12

12

10

11

10

9

8

7

6

4

4

2

2 и 31

13

30

28

30

28

28

26

26

25

23

23

21

21

14

19

18

19

18

17

16

15

14

12

12

10

10

15

9

7

9

7

7

5

5

3

2

1 и 31

29

29

16

27

26

27

25

25

23

23

21

20

19

18

17

17

16

14

16

14

14

12

12

11

9

9

7

7

18

5

4

5

4

3

2

1 и 31

29

28

27

26

26

19

24

23

24

23

22

21

20

19

17

17

15

15


Ярлык хана Тулун-бека митрополиту Михаилу датирован следующим образом: "овечия лета дарыка (т. е. летосчисления) в 708 лето солгата месяца в десятый нова". 708 г. эры гиджры = 1308--1309 г. н. э. (см. таблицу XXIV). Но эта дата явно невозможна для времени Тулун-бека, который жил значительно позднее. Надо предположить, что первоначально в тексте было не 708, а 780. Действительно, буквенное обозначение двух цифр -- 8 (И) и 80(П) чрезвычайно сходно и поэтому возможно допустить, что при переписке произошла ошибка: вместо YП (780) появилось: YИ (708). 780 г. эры гиджры соответствует 1378 -- 78 гг. н. э. (см. таблицу XXIV), под словом "солгат", повидимому, следует подразумевать испорченное "зу-л-каде" -- одиннадцатый месяц мусульманского календаря. Поскольку новогодие (1 мухаррама) 780 г. падает на 30 апреля 1378 г., постольку 1 зул-каде 780 г. придется 18 февраля 1379 г. (см. таблицу XXIII--XXIV). Число месяца указано по монгольскому календарному счету: "десятый (день) нова", т. е. десятый день первой половины месяца, именно -- 27 февраля. 1379 г. был действительно годом овцы, как это и указано в источнике, и эта дата вполне совпадает с временем Тулун-бека.

-88-

        Так приходится разрешать вопросы, связанные с переводом на нашу эру дат комбинированной системы летосчисления, в которой имеются элементы и мусульманского, и тюрко-монгольского счета.

 V. ЗАКЛЮЧЕНИЕ

         § 1. Значение хронологии как вспомогательной исторической дисциплины. Чтобы оценить в должной мере значение хронологии, как вспомогательной исторической дисциплины, приведем несколько примеров, из которых станет ясно, что только при очень серьезном и умелом пользовании теми приемами определения и уточнения дат, которым нас учит хронология, мы имеем возможность установить время ряда первостепенных исторических событий. Когда мы раскрываем, например, учебник для исторических вузов по истории СССР до XVIII в. и в конце его находим стройную таблицу главнейших дат, у нас остается впечатление, что дело с хронологией обстоит легко и просто. Все даты, имеющие значение, известны, собраны в учебнике, и остается лишь закрепить их в своей памяти. Но мы забываем при этом, что не только нигде в первоисточниках нельзя встретить подобной цельной систематизированной хронологической таблицы, но мы не найдем даже в готовом виде и дат отдельных событий. Их приходится еще устанавливать, и здесь-то вступает в свои права хронология, как вспомогательная историческая дисциплина. Насколько важно в этом отношении в совершенстве владеть научными методами исследовательской техники, видно из того, что по поводу дат ряда событий идут научные споры. Разрешить их дает возможность только детальный и правильно поставленный анализ соответствующих источников в тех направлениях, которые нам указаны специальной вспомогательной исторической дисциплиной -- хронологией.
        В качестве примера остановимся только на трех датах: договора Олега с Византией, похода кн. Игоря Святославича против половцев, о котором говорит уникальный художественный памятник Киевской Руси -- "Слово о полку Игореве", и битвы на Калке.
        Это -- события большого исторического значения, и стоит потрудиться над уточнением вопроса о времени, к которому они относятся.
        Начнем с договора Олега с Византией. В учебнике указано, что он был заключен в 911 г. Но некоторые ученые, и среди них очень авторитетные, признавали правильным датировать договор 912 г. Почему такие разногласия и какой дате отдать предпочтение? Для решения этого вопроса обратимся к источникам.
        Договор Олега сохранился в двух древнейших списках летописи -- Лаврентьевском и Ипатьевском. Помещен он под 6420 г. При этом точная дата сформулирована следующим образом: "сентября в 2, а в неделю 15, в лето создания миру 6420". При

-89-

переводе на нашу эру естественно возникает вопрос о том календарном стиле, которым пользовался летописец. Если это мартовский стиль, то сентябрь 6420 г. (византийского летосчисления соответствует 912 г. нашей эры (6420 -- 5508). При сентябрьском счете речь, очевидно, идет о 911 г. (6420 -- 5509). Именно в вопросе о календарном стиле и кроются причины разногласий ученых по поводу даты договора.
        Но как выяснить, каким именно стилем пользовался летописец? Вчитаемся в дату. Договор заключен "сентября в 2, а в неделю 15". Неделя -- воскресенье. Не вполне ясные указания договора можно расшифровать в четырех направлениях: 1) дело происходило в воскресенье 2 сентября, которое (воскресенье) являлось 15 по счету в данном (мартовском или сентябрьском) году; 2) дело происходило 15 сентября в воскресенье, которое являлось вторым но счету в данном (мартовском или сентябрьском) году; 3) "возможно, что после цифры 15 пропущено слово "индикта", --тогда смысл текста таков -- дело происходило в воскресенье 2 сентября, в году, индикт которого равен 15; 4) возможно, что слово "неделя" поставлено ошибочно вместо "индикт" -- следовательно, дело происходило 2 сентября (день недели неизвестен) в том году, индикт которого равен 15.
        Проверяя последовательно все три предположения, убеждаемся, что первое из них явно невозможно, т. к. в мартовском году 15 воскресенье от начала года пришлось бы в июне, в сентябрьском -- в декабре, но ни в том, ни в другом случае, никак не могло быть в сентябре. Кроме того, таблицы IX -- X легко нас убеждают, что 2 сентября вообще не совпадало в 6420 г. с воскресеньем ни по мартовскому, ни по сентябрьскому календарному стилю. По этой же причине приходится отбросить и третий вариант. Второй вариант должен быть отвергнут в силу того, что хотя, судя по таблицам IX -- X, 15 сентября в 6420 (сентябрьском) году и было воскресенье, но не второе, а третье от начала года. Приходится остановиться на четвертом варианте. Если договор не указывал, на какой день недели приходилось 2 сентября, а речь шла только о 15 индикте (слово "неделя" вместо "индикт" ошибочно появилось уже позднее), то 15 индикт (как показывает таблица V) действительно совпадает с 6420 (сентябрьским) годом. При подобном допущении 2 сентября 6420 г. от "сотворения мира" = 2 сентября 911 г. н. э. (6420 -- 5509). Вот такой сложный путь должен пройти исследователь для уточнения даты интересующего его события, при чем, как мы могли убедиться, без знания вспомогательной исторической дисциплины -- хронологии он не смог бы ориентироваться на этом пути.
        Второй пример: поход Игоря Святославича помещен в Лаврентьевской летописи под 6693 г., "в Ипатьевской -- под 6694 г. Почему такое расхождение в датах? Объясняется ли оно тем, что летописцы пользуются при датировке различными календарными стилями, или же тем, что они намеренно относят это событие к различным годам. В этом случае, очевидно, важно выяснить, какая летопись ошибается.

-90-

        В Ипатьевской летописи рассказывается в связи с описанием похода Игоря, что в мае 6694 г. было солнечное затмение. В зависимости от календарной системы, май 6694 г. может соответствовать или 1185 г. н. э. (при ультра-мартовском стиле: 6694 -5509 = 1185) или 1186 г. н. э. (при мартовском и сентябрьском стилях: 6694 - 5508 = 1186). По таблицам XVII--XIX убеждаемся, что затмение солнца имело место в мае 1185 г. (ультра-мартовский стиль). Эта дата соответствует показаниям Лаврентьевской летописи, пользующейся мартовским стилем (6693 - 5508 = 1185).
        Обращаемся к выяснению даты битвы на Калке. Различные летописцы по разному датируют это событие, называя следующие годы: 6731, 6732, 6733 и 6734. Учитывая возможность пользования со стороны летописцев тремя календарными стилями (сентябрьским, мартовским и ультра-мартовским), в зависимости от чего при переводе дат от "сотворения мира" на современное летосчисление приходится вычитать одно из трех чисел (5507, 5508 и 5509), мы приходим к выводу, что названным выше четырем датам византийского летосчисления соответствуют шесть возможных дат н. э.: 1222 г., 1223 г., 1224 г., 1225 г., 1226 г., 1227 г. Выбирая между ними, очевидно следует итти путем исключения.
        Летописцы неодинаковым образом указывают также день битвы. По разноречивым показаниям, битва происходила или
        30 мая, или 31 мая, или 16 июня, при этом те известия, которые говорят о мае, приурочивают день битвы к празднику св. Еремия. Последний, как показывает календарь, приходился именно на 31 мая, таким образом, дата 30 мая отпадает, как явно ошибочная. Исследователю приходится колебаться только между двумя возможными днями: 31 мая и 16 июня. Но поскольку дело происходило во всяком случае или в июне или в мае, постольку при переводе той или иной из вышеприведенных дат с византийского летосчисления на нашу эру, при любом календарном стиле отпадает в качестве вычитаемого число 5507. Следовательно, шесть возможных дат н. э. (1222--1227) приходится сократить до пяти (1222--1226), исключив 1227 г., как явно неприемлемый.
        В некоторых летописях указано, что переправа князей через Днепр, -- предшествовавшая битве на Калке, произошла во вторник за 8 или 9 дней до самой битвы. Учитывая, что битва могла быть или 31 мая, или 16 июня, очевидно следует проверить, в каких из пяти указанных выше годов (1222--1226) день недели, на 8--9 или даже 10 (принимая во внимание неточность расчетов) суток, предшествовавший 31 мая или 16 июня, был вторником. По таблицам IX--X выясняем, что при допущении днем битвы 31 мая, это могло быть в 1223 и 1224 годах. Если же предположить, что битва случилась 16 июня, то в таком случае, как легко убедиться из тех же таблиц, предварительная (за 8--10 суток) переправа могла быть во вторник в 1222 и 1223 года. Таким образом, новая проверка заставляет нас отказаться при датировке битвы на Калке от 1225 и 1226 г. Очевидно, событие имело место 31 мая 1223 или 1224 г. или же 16 июня 1222 или 1223 г.
        Случайно сохранившееся в работах известного историка Карамзина

-91-

указание, что днем битвы на Калке была пятница, позволяет еще более сузить круг дат, из которых нам приходится выбирать. Из двух лет (1223 и 1224), останавливаемся на последнем годе, т. к. именно тогда 31 мая приходилось в пятницу. Выбор между 1222 и 1223 годами решаем в пользу 1223 г., когда пятница совпадала с 16 июня.
        Итак, метод исключения в конечном итоге заставляет сосредоточить свое внимание только на двух датах: 31 мая 1224 г. и 16 июня 1223 г. Какая же из них является наиболее вероятной? Русские источники не дают ответа на этот вопрос, в силу чего приходятся обращаться к данным мусульманских писателей. Один из них, Ибн-Эльасир, датирует битву на Калке 620 г. эры гиджры. В переводе на современное летосчисление (см. таблицы XXIII --XXIV) получим период с 4 февраля 1223 г, по 23 января 1224 г. Из двух дат, выведенных выше на основании русских источников для битвы на Калке, в эти пределы укладывается только дата 16 июня 1223 г.
        Приведенные выше примеры должны были наглядно показать, какое громадное значение имеет хронология, как вспомогательная историческая дисциплина, для определения дат исторических событий.
        Основательное знакомство с хронологией оказывает громадную помощь для понимания содержания документа, его классовой сущности. Сроки уплаты денег в заемных кабалах часто указывались не числовою датою, а названием праздника или дня памяти святого. Вот перед нами кабала, данная старухой-вогулкой со внуком, под залог пашни и луга, оцененных в 100 рублей. На первый взгляд названная кабала ничем не отличается от тысячи таких же кабальных записей. Но если учесть сроки совершения сделки -- 16 марта и уплаты долга -- "благовещеньев день", т. е. 25 марта того же года, -- всего 9 дней до уплаты, -- то злостный, ростовщический характер сделки становится очевидным.
         § 2. Литература по хронологии.
        Укажем специальные работы по различным вопросам хронологии для лиц, желающих углубить свои знания в этой области.
        Общие обзоры, в популярной форме, систем летосчисления у различных народов в различные эпохи дают работы В. К. Никольского, "Происхождение нашего летосчисления" (М., 1938) и Н. И. Идельсона, "История календаря" (Л., 1925).
        Для получения более специальных сведений следует обратиться к фундаментальным трудам по хронологии на иностранных языках. На немецком языке в первую очередь должны быть рекомендованы исчерпывающие труды Шрама, "Вспомогательные таблицы по хронологии" (Schram, R. "Hilfstafeln fur Chronologie", Wien, 1907) и Гинцеля, "Руководство по математической и технической хронологии" (Ginzel, F. K. Handbuch fur mathematischen und technischen Chronologie, Bd. 1--4, 1906--1914). Из работ французских авторов заслуживают внимания "Хронология" Кавеньяка (Cavaignac, Е. "La chronologie" Paris, 1934) и большой специальный раздел по

-92-

хронологии, помещенный в руководстве по дипломатике Жири (Giry, Manuel de diplomatique, Paris, 1894, рр. 83--275).
        Сводной работой, справочного характера, охватывающей различные проблемы древне-русской хронологии, является книга Н. В. Степанова, "Календарно-хронологический справочник". (Чтения в Московском Обществе истории и древностей российских, 1917 г., кн. 1). В исследовании того же автора "Новый стиль и православная пасхалия" (М., 1907) рассматривается весь круг вопросов, связанных с вычислением православной пасхи.
        Не будем здесь называть остальных многочисленных работ Н. В. Степанова, посвященных выяснению систем летосчисления различных русских летописных сводов и других исторических памятников нашего прошлого.
        Наряду со Степановым, большой вклад в изучение вопросов древне-русской хронологии сделал Д. О. Святский, книга которого "Астрономические явления в русских летописях" (М., 1917) дает научную основу изучения летописных известий о солнечных и лунных затмениях, кометах, метеорах, падающих, звездах и. пр.
        Ряд таблиц, составленных Степановым и Святоким, приведен в настоящем пособии.
        Отдельно формулы для решения задач по хронологии разработаны Д. М. Перевощиковым, "Правила времясчисления, принятого православною церковью" (М., 1880) и Н. И. Черухиным, "Календарь для хронологических справок" (журн. "Русская Старина", 1873 г., N 7).
        До сих пор не утратила своего значения старая работа Д.И.Прозоровского: "О старинном русском счислении часов" (Труды 2-го Археологического съезда, вып. 2, Спб., 1881, стр. 105--194). На основе анализа многочисленных источников, Прозоровский делает попытку выяснить систему деления времени на часы в до-Петровской Руси. Некоторые его данные, сведенные в таблицы, приведены в соответствующем разделе настоящего пособия.
        Вопросам, связанным с изучением особенностей летописной хронологии, посвящены две статьи А. А. Шахматова: 1) "Исходная точка летосчисления "Повести временных лет" (Журн. Мин. Нар. Просв., 1897 г., N 3) и 2) "Хронология древнейших русских летописных сводов" (Журн. Мин. Нар. Проев., 1897, N 4).
        Материал по хронологии народов СССР отчасти имеется в основной работе Степанова (системы летосчисления: грузинская, армянская, мусульманская). Дополнительно могут быть указаны некоторые специальные пособия.
        Занимавшийся русско-ливонскими источниками А. Е. Энгельман написал "Хронологические исследования в области русской и ливонской истории" (Спб., 1858).
        Вопросы грузинской хронологии разрабатывал М. И. Броссе (Бюллетень Академии наук, т. XXII).
        Есть специальное исследование по "восточной хронологии" Н. Ф. Катанова, напечатанное в N 1 "Известий Северо-восточного Археологического Института в Казани" (Казань, 1920). Но работой

-93-

этой нужно пользоваться с осторожностью, так как в ней есть ряд погрешностей.
        Известный востоковед А. М. Позднеев издал "Монгольскую летопись Эрдэнийн Эрихэ" (Спб., 1883). В ней широко используется тюрко-монгольcкий циклический счет. В предисловии к летописному тексту даны основы тюрко-монгольской хронологии, а в конце помещена таблица животного цикла. Составленная на монгольском, манчжурском и китайском языках, она была недоступна для пользования. В настоящем руководстве указанная таблица дана в русском переводе (Н. В. Устюгова) и переработке.
        Взаимоотношение мусульманского и тюрко-монгольского счета применительно к ханским ярлыкам XIII-XIV вв.. изучено в работах В. В. Григорьева "О достоверности ярлыков, данных ханами Золотой Орды русскому духовенству", М., 1842, и М. Д. Приселкова, "Ханские ярлыки русским митрополитам", Пг., 1916.
        В качестве иллюстрации для заключительной части пособия на конкретном примере значения хронологии, как вспомогательной исторической дисциплины, может быть рекомендована статья А. Б. Салтыкова "Хронология битвы на р. Калке" (Ученые записки Института Истории РАНИИОН, т. 4, М., 1929). Правда, конечный вывод автора нуждается в исправлении.
        В библиотеке Московского Историко-Архивного института имеется размноженное на стеклографе на правах рукописи учебное пособие по хронологии Н. В. Устюгова, которое было нами использовано.

-94-

 

НА СТРАНИЦУ АВТОРА

НА ГЛАВНУЮ СТРАНИЦУ САЙТА

 

 

Все материалы библиотеки охраняются авторским правом и являются интеллектуальной собственностью их авторов.

Все материалы библиотеки получены из общедоступных источников либо непосредственно от их авторов.

Размещение материалов в библиотеке является их цитированием в целях обеспечения сохранности и доступности научной информации, а не перепечаткой либо воспроизведением в какой-либо иной форме.

Любое использование материалов библиотеки без ссылки на их авторов, источники и библиотеку запрещено.

Запрещено использование материалов библиотеки в коммерческих целях.

 

Учредитель и хранитель библиотеки «РусАрх»,

академик Российской академии художеств

Сергей Вольфгангович Заграевский