|
РусАрх |
Электронная научная библиотека по истории древнерусской архитектуры
|
Источник: Ефимов А.П. Три взгляда на акустику помещений. В журн. Install-pro. №№ 3-7, 2000 г. Все права сохранены.
Размещение электронной версии в открытом доступе произведено: http://www.install-pro.ru. Все права сохранены.
Размещение в библиотеке «РусАрх»: 2011 г .
А.П. Ефимов
Три взгляда на акустику помещений
Введение
 Современному инженеру в
практической деятельности приходится иметь дело с проектированием и
эксплуатацией студий звукозаписи, звукового и телевизионного
вещания, систем и устройств звукоусиления в производственных помещениях,
аудиториях, театральных и концертных задах. В связи с этим ему
необходимо знать и понимать основные положения акустики помещений
(строительной, архитектурной акустики) и применять эти положения при решении
возникающих задач.
Современному инженеру в
практической деятельности приходится иметь дело с проектированием и
эксплуатацией студий звукозаписи, звукового и телевизионного
вещания, систем и устройств звукоусиления в производственных помещениях,
аудиториях, театральных и концертных задах. В связи с этим ему
необходимо знать и понимать основные положения акустики помещений
(строительной, архитектурной акустики) и применять эти положения при решении
возникающих задач.
Цель статьи - ознакомить с историей, развитием и сов-ременным состоянием этой важной отрасли акустики как науки, дать некоторые знания, которые могут понадобиться при выполнении проектов, частью которых является акустический расчет перечисленных объектов.
Истоки архитектурной (строительной) акустики восходят к глубокой древности. Акустические задачи в те времена ставились и решались в связи со строительством гигантских сначала культовых, а позже и других общественных сооружений - залов для собраний и зрелищ.
Зодчие Ассирии, Вавилона, Древнего Египта в V-II тысячелетиях до н. э. строили храмы, обладавшие выразительной архитектурой и впечатляющим художественным убранством. И мощные строительные конструкции, и скульптура, и живопись - все было направлено на то, чтобы поразить и подавить психику молящихся, создать у них ощущение своего ничтожества, мистического страха перед божественными силами. Зодчим, по-видимому, уже были известны законы распространения и отражения звуковых волн. Пользуясь ими, они достигали акустических эффектов, поражавших воображение молящихся.
Иные, хотя и столь же сильные чувства возбуждало искусство Древней Греции (VII-IV вв. до н. э.) - одной из вершин мировой цивилизации. В отличие от искусства Древнего Египта в основе древнегреческого лежало представление о силе и красоте человека, его неразрывной связи с окружающей природой и общественной средой. Искусство Древней Греции отличалось гармоничностью и светлыми чувствами. Древним греческим храмам и другим общественным сооружениям свойственна соразмерность частей, она определила их высокие акустические свойства. Рациональность принятых древними греками акустических решений была впоследствии подтверждена наукой нашего времени.
Наряду с храмовыми зданиями уделялось большое внимание сооружениям общественного назначения. Зрелищные сооружения Древней Греции разделялись на два вида: одейоны и театры. Первые представляли собой сравнительно небольшие крытые здания для репетиций и представлений с малым количеством исполнителей (без хора) и зрителей, вторые являлись зрелищными сооружениями открытого типа и большой вместимости (тысячи и десятки тысяч человек). Каменные скамьи зрительских мест располагались на склонах возвышенностей.
Традиции греческих архитекторов были продолжены их римскими последователя в VII-I вв. до нашей эры. Римские театры на открытом воздухе были сходны с греческими, хотя в отличие от них строились не только на естественных склонах, но и на горизонтальных участках. Типичным примером такого театра служит амфитеатр Флавия - Колизей на 56 тыс. зрителей, построенный в 80-90 гг. н. э.
В наше время требуется установка систем звукоусиления даже в залах вместимостью 200-300 человек. Поэтому кажутся фантастическими свидетельства историков о вместимости древних греческих и римских театров, обслуживающихся естественной звучностью голосов актеров. Так, театр Помпея вмещал 17800 человек, театр Марцелла в Риме - 20 тыс. человек. Если даже эти данные сильно преувеличены (по современным оценкам, названные театры вмещали соответственно 5 и 7 тыс. человек), то кажется чудом, что в этих гигантских театрах достигали удовлетворительной звучности на слушательских местах. Остается предположить: либо уши тогдашних посетителей зрелищ были в несколько раз чувствительнее современных, либо древние строители знали неведомые нам секреты, позволявшие получить достаточную громкость и разборчивость на слушательских местах. Известно, что в маски актеров, изображающие различные эмоции действующих лиц, были встроены рупоры, направлявшие звук в сторону зрителей.
Римский поэт, философ, ученый Лукреций Кар (99-55 гг. до н. э.) в трактате "О природе вещей" выразил тогдашние представления об акустике, в том числе и об акустике помещений. Витрувий в "Десяти книгах об архитектуре" обобщил опыт античных архитекторов и сформулировал ряд положений, которые являются гениальным предвидением и используются при строительстве современных театров. Наши далекие предки имели ясное представление о роли прямого звука, опасности поздних отражений, способных вызвать эхо, и о "нарушении строения звуковых волн", вызванных отражениями звуков от преград.
Знание акустических явлений в помещениях находило подчас самое необычное применение. До наших дней дошли так называемые "шепчущие галереи" Древнего Рима и Китая. В них, благодаря умело расставленным и особым образом ориентированным отражающим поверхностям стен, тихие звуки распространялись на большие расстояния, и люди, удаленные друг от друга на десятки метров, могли общаться, не напрягая голоса.
 Вблизи г. Сиракузы на
острове Сицилия сохранились древние каменоломни. По преданию, в одну из
галерей, названную "ухом Диониса", помещали пленных. Наверху благодаря
естественным каналам-щелям было слышно все, что пленные говорили между собой.
Таким образом выведывались их секреты.
Вблизи г. Сиракузы на
острове Сицилия сохранились древние каменоломни. По преданию, в одну из
галерей, названную "ухом Диониса", помещали пленных. Наверху благодаря
естественным каналам-щелям было слышно все, что пленные говорили между собой.
Таким образом выведывались их секреты.
Особые звуковые каналы позволяли правителям в своих дворцах подслушивать откровенные высказывания сановников, полагавших, что их не слышат, и на основании этого оценивалась их преданность.
В конце
дохристианской эры развитие акустики как экспериментальной части физики
приостановилось. Считалось, что немалую роль в этом сыграл авторитет греческого
ученого Аристотеля (384-
Античные знания об акустике помещений нашли практическое применение при сооружении культовых зданий раннего и позднего средневековья. В католических храмах создавалось впечатление музыки, льющейся с небес. Это не случайная находка строителей, а сознательное использование особых архитектурных форм и продуманное расположение духового органа и хора. Своеобразными акустическими эффектами отличались и православные храмы. Голоса священника и певчих отражались от купольной части сооружения вниз, к молящимся, и у них возникало ощущение общения с небом. Для создания желаемой акустической среды строители закладывали в стены и своды храмов глиняные кувшины разных размеров, так называемые "голосники". Это были своеобразные акустические резонаторы.
В 18 и начале 19 в. внимание стали уделять сооружению концертных и театральных залов. Развивалось синтетическое музыкальное искусство - опера. Разумным выбором геометрической формы, размеров, продуманным размещением звукопоглощающих материалов в этих залах создавали хорошие условия для слушателей и исполнителей - певцов, музыкантов.
 В 19 в. из не вполне
четких представлений античного мира стали выкристаллизовываться точные знания.
Эйлер, Лагранж, Фурье, Стокс, Юнг, Гельмгольц, Дж. Стретт (последний более
известен под именем лорда Рэлея, точнее Рейли) создали акустику как науку. В
конце 19 и начале 20 в. У. Сэбин (Walles Sabine) выполнил эксперименты,
положившие начало теории архитектурной акустики, выявил количественные связи
между геометрическими параметрами помещений и их акустическими
характеристиками. Его работы были продолжены другими.
В 19 в. из не вполне
четких представлений античного мира стали выкристаллизовываться точные знания.
Эйлер, Лагранж, Фурье, Стокс, Юнг, Гельмгольц, Дж. Стретт (последний более
известен под именем лорда Рэлея, точнее Рейли) создали акустику как науку. В
конце 19 и начале 20 в. У. Сэбин (Walles Sabine) выполнил эксперименты,
положившие начало теории архитектурной акустики, выявил количественные связи
между геометрическими параметрами помещений и их акустическими
характеристиками. Его работы были продолжены другими.
Эйринг, Хант, Беранек, Ма Да-ю, Кнудсен, Майер, Ватсон создали солидный теоретический фундамент современной акустики помещений. Заметный вклад в архитектурную акустику внесли отечественные ученые: И.И. Андреев, И.Г. Дрейзен, А.Н. Качерович, С.Я. Лифшищ, А.В. Рабинович, С.Н. Ржевкин, М.А. Сапожков, В.В. Фурдуев и другие.
Сэбин рассматривал акустические процессы в помещении после выключения источника звука как запаздывание многократно отраженных волн и их постепенное ослабление в результате поглощения энергии волн преградами. Исходной причиной этого процесса является энергия, сообщенная помещению источником звука.
Теория У.
Сэбина, несмотря на большие практические успехи, вызвала серьезную критику. В
До начала 20 в., т. е. до работ У. Сэбина, главное внимание в акустике помещений уделяли анализу направлений путей распространения потоков звуковой энергии в помещении - прямого и отраженного от преград, т. е. рассмотрению геометрической (лучевой) картины. Геометрическая теория - самая древняя. Она успешно применяется и в наше время, особенно при проектировании залов большой вместимости. Геометричес-кая теория получила развитие в работах И.Г. Дрейзена, А.Н. Качеровича, Л. Контюри. С.Я. Лифшица. Е. Скучика и других.
В настоящее время не существует единой теории, объясняющей все акустические процессы в помещениях и позволяющей с единых позиций решать конкретные задачи оптимизации в помещениях разного назначения. К тому же эти задачи связаны с психофизиологией и эстетической оценкой звучания слушателями, со вкусами музыкантов и актеров. Такие задачи носят особый характер, и мы не будем их касаться. Проблемы акустики залов большой вместимости, оборудованных системами звукоусиления, также находятся за пределами данной статьи. Она посвящена лишь рассмотрению основных положений и практическому применению трех существующих теорий - статистической, волновой, геометрической.
Статистическая теория
|
|
|
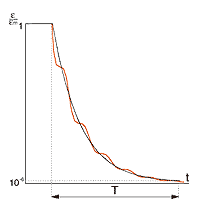
Рис. 1а. Процесс спада звуковой энергии |
Основные положения. В статистической теории акустические процессы в помещении рассматриваются как постепенный спад энергии многократно отраженных преградами помещения волн. Этот спад происходит после прекращения действия источника звука. Идеализируя, считают этот процесс в первом приближении непрерывным. Тогда его можно изобразить в линейном масштабе экспонентой (рис.1,а), а в полулогарифмическом масштабе - прямой (рис 1,б). Предпосылкой к такому рассмотрению является выполнение двух условий: все направления движения волн равновероятны, а плотность звуковой энергии e = Е / V в каждой точке пространства помещения одинакова.
|
|
|
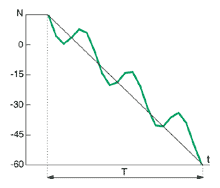
Рис. 1б. Процесс спада звуковой энергии в полулогарифмическом масштабе |
Прежде чем анализировать процесс спада звуковой энергии в помещении, необходимо объяснить, почему в архитектурной акустике большее внимание уделяется не стационарному процессу (процессу установившихся колебаний), а переходному (нестационарному). Последний начинается после прекращения действия источника звука, заключается в постепенном спаде звучания вследствие потерь звуковой энергии и называется отзвуком, или реверберацией.
Реверберация существенно влияет на качество и речевого, и музыкального звучания. Чрезмерная длительность реверберации приводит к тому, что новые слоги речи звучат на фоне предыдущих затухающих слогов. Разборчивость речи при этом ухудшается. При коротком отзвуке разборчивость речи вполне удовлетворительна, но своеобразная "безжизненность", "стерильность" такого звучания воспринимается так же, как не-достаток, особенно при художественном чтении. Еще большее значение имеет процесс отзвука при слушании музыки. Каждая музыкальная фраза представляет собой последовательность звуковых импульсов. Затянутый отзвук нарушает эстетичность восприятия музыки тем сильнее, чем быстрее темп исполнения, так как звуки "набегают" друг на друга. Наоборот, при очень коротком отзвуке или его отсутствии (при исполнении на открытом воздухе) музыка звучит сухо. Утрачивается слитность звучания. Лишь при некотором, вполне определенном для каждого стиля исполнения времени отзвука образуется необходимая связность звучания, создающая наилучший эстетический результат.
|
|
|
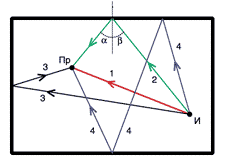
Рис. 2. Прямой и отраженные сигналы |
Рассмотрим процессы, происходящие в помещении при звучании источника И (рис. 2). Первым в точку приема Пр, где находятся уши слушателя или микрофон, приходит по пути 1 прямой звук, затем по пути 2 звуки, отраженные от ближайших к источнику поверхностей, далее звуки по пути 3, отраженные от удаленных поверхностей. Позже приходят звуки, претерпевшие двукратные отражения на пути 4, и т. д. Количество отражений в единицу времени возрастает пропорционально второй степени времени. Помещение постепенно заполняется звуковой энергией. После прекращения звучания источника начинается процесс отзвука. В той же последовательности, как и при начале звучания, сперва в точку приема приходят сравнительно редкие начальные отражения. Далее плотность запаздывающих импульсов увеличивается, а их энергия постепенно спадает (рис. 3).
|
|
|
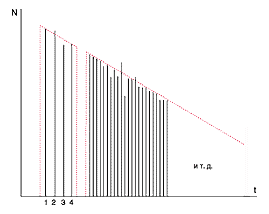
Рис. 3. Структура ранних отражений |
Статистическая теория занимается именно этой, второй частью отзвука с повышающейся плотностью импульсов во времени и уменьшающейся их энергией. Прямой звук и начальные сравнительно редкие отражения статистической теорией не принимаются во внимание.
Метод, предложенный У. Сэбином, основан на модели идеального помещения, в котором звуковое поле после прекращения действия звукового сигнала может быть рассчитано на основе статистического рассмотрения процесса затухания звука. При этом предполагается, что амплитуды и фазы отраженных звуковых волн распределены хаотически, т. е. в волновом движении нет преобладающих направлений потоков и симметрии в распределении амплитуд. Принятое допущение позволяет считать, что средние значения звуковой энергии по различным направлениям одинаковы, т. е. звуковое поле изотропно, и средняя по времени плотность звуковой энергии в любой точке помещения тоже одинакова. Такое звуковое поле называют диффузным. Его рассмотрение дало возможность пренебречь явлениями интерференции и применить при расчетах энергетическое суммирование. Этот подход подобен используемому в кинетической теории газов и основан на математической теории вероятностей. Л. Бреховских показал, что для помещений, линейные размеры которых велики по сравнению с длиной волны, получаются достаточно удовлетворительные результаты.
Методами математической статистики в диффузном поле определяют среднюю длину пробега звукового луча между двумя отражениями. Для помещения в форме прямоугольного параллелепипеда с линейными размерами, близкими к "золотому сечению" (длина относится к ширине и к высоте, как 2 : 20,5 : 1, по другому определению 5 : 3 : 2), статистически определенная средняя длина свободного пробега звукового луча
lср = 4V / S ,
где V - объем помещения, S - общая площадь всех ограничивающих поверхностей (пола, потолка, стен).
Впоследствии было установлено, что полученная зависимость примерно сохраняется и для помещений, линейные размеры которых отклоняются от "золотого сечения", и для помещений более сложной формы.
При каждом отражении часть падающей энергии поглощается преградами и превращается в тепло. Процесс постепенного уменьшения плотности звуковой энергии У. Сэбин назвал реверберацией (reverberation в переводе означает "отражение", "отзвук"). В Германии для обозначения этого процесса используется слово Nachhall, в переводе на русский "отзвук", "отголосок", "отклик". Термин "отзвук" ранее встречался и в русской технической литературе.
За длительность процесса, реверберации - время реверберации - было принято считать промежуток, за который плотность звуковой энергии уменьшается в 106 раз, звуковое давление в 103, а уровень звукового давления на 60 дБ.
Прямых объяснений мотивов выбора спада уровня на 60 дБ нет. Попытаемся найти разумные причины. Фортиссимо оркестра соответствуют уровни звукового давления 90-100 дБ, а пианиссимо - 35-40 дБ. Тогда средние уровни составят 63-70 дБ и принятое по определению (спад на 60 дБ) время реверберации будет примерно соответствовать длительности спада средних уровней до порога слышимости. Возможно, данное обстоятельство и стало причиной выбора такого определения времени реверберации.
Разумеется, все это справедливо в отсутствии акустических помех. При шумах, например, с уровнями 30-40 дБ, что характерно и для жилой комнаты, и для концертного зала, значительная часть отзвука будет маскироваться шумами, и слышимый отзвук будет длиться менее половины времени реверберации.
Расчетные соотношения. Для экспериментального определения времени реверберации Сэбин пользовался простейшими приспособлениями: органными трубами как источником звука и секундомером. Он нашел, что время реверберации Т прямо пропорционально объему помещения V и обратно пропорционально произведению среднего коэффициента поглощения aср и площади всех преград S:
![]()
Средний коэффициент поглощения:
![]()
где a1, a2,... - коэффициенты поглощения различных материалов;
S = S1 + S2 + ... - общая площадь преград; n - количество разных преград.
Из этого
выражения можно заключить, что средний коэффициент поглощения соответствует
единому материалу, которым можно было бы покрыть все поверхности преград
помещения с сохранением общего звукопоглощения А = aсрS.
Единицей поглощения считают
 По измерениям времени реверберации
в пяти различных помещениях в форме прямоугольного параллелепипеда и объемами
от 96 до
По измерениям времени реверберации
в пяти различных помещениях в форме прямоугольного параллелепипеда и объемами
от 96 до
В дальнейшем было обнаружено, что k различно для помещений разной формы. Измеренные значения k приведены в таблице.
|
Форма помещения |
k |
|
Крестообразное в плане, с куполообразным потолком |
0,177 |
|
Близкое к "золотому сечению" |
0,164 |
|
Трапециевидное в плане, театрального типа |
0,160 |
|
Кубической формы |
0,157 |
|
Очень широкое в плане, с низким потолком |
0,152 |
Из приведенных примеров видно, что форма помещения влияет на значение времени реверберации, хотя из структуры самой формулы У. Сэбина это не вытекает. Дело в том, что от соотношения линейных размеров зависит средняя длина пробега между двумя отражениями lcр, следовательно, зависит и время реверберации Т.
Теоретический вывод формулы Сэбина основан на предположении о диффузном, равномерном распределении звуковой энергии по пространству помещения и о непрерывном поглощении энергии преградами в процессе реверберации.
Это допущение дает сравнительно небольшое отклонение рассчитанной величины Т от измеренной, если средний коэффициент поглощения мал, и поэтому количество отражений получается достаточно большим, чтобы пренебречь дискретностью этого процесса.
На самом деле звуковая энергия поглощается преградами не непрерывно, а скачками, по мере достижения волной той или иной поверхности. Поэтому вполне равномерного заполнения энергией всего объема по-мещения не будет.
Более точные
исследования реверберации были проведены в
![]()
Разложив выражение ln(1-a) в ряд и оставив в нем ввиду малости a только первый член, обнаружим, что при небольших значениях a формула Эйринга переходит в формулу Сэбина. Действительно,
![]()
Объясним смысл знака минус в знаменателе формулы. Логарифм чисел меньше единицы имеет отрицательное значение. Знак минус введен, чтобы исключить физическую несообразность - отрицательное значение Т. Выражение, стоящее в знаменателе, является эквивалентом общего поглощения А = aсрS, содержащегося в формуле Сэбина.
Сравнивая формулы Сэбина и Эйринга, приходим к выводу, что приближение Сэбина дает завышенное значение T. Расхождение увеличивается с возрастанием aср:
|
aср |
0,2 |
0,5 |
0,8 |
|
Завышение Т, % |
11 |
37 |
100 |
При значении aср = 1 получается физически нереальный результат: T= V/6S, хотя в этом случае должно Т = 0.
Формулы Сэбина и Эйринга могут быть применены, если звукопоглощающие материалы распределены по ограждающим помещение поверхностям достаточно равномерно, чтобы можно было пользоваться понятием среднего коэффициента поглощения.
Для оптимизации акустических условий в концертных залах рекомендуется aср = 0,19. Поэтому вполне допустимо время реверберации в этом случае рассчитывать по формуле Сэбина.
При выводе формулы Сэбина и Эйринга приняты некоторые допущения, которые редко оговариваются в литературе по акустике. Формула Сэбина получена в предположении, что волны падают на преграды под любыми углами, а при выводе формулы Эйринга принято, что волны падают на преграды под углами, близкими к нормали. Поэтому, строго говоря, в формулу Сэбина следовало бы подставлять значения коэффициента поглощения, определенные в диффузном поле, в реверберационной камере, а в формулу Эйринга - значения коэффициента поглощения, измеренные в плоском поле, при нормальном падении, т. е. в трубе.
При очень неравномерном распределении общего поглощения результат, вычисленный по формуле Эйринга, может оказаться далеким от измеренного. Миллингтон (Millington) объяснил причину этого расхожде-ния. Эйринг полагал, что число отражений от разных поверхностей с площадями S1, S2,... одинаково. В действительности вероятность числа отражений от данной поверхности тем больше, чем больше сама поверхность. На основании этих соображений Миллингтон вывел иную формулу для расчета времени реверберации:
![]()
где Si - площадь материалов с коэффициентами поглощения ai.
Недостаток формулы Миллингтона заключается в следующем: вычисленное значение времени реверберации получается равным нулю, если хотя бы один элемент преграды, как бы он ни был мал, имеет aср = 1. По-видимому, при выводе формулы было принято какоето сомнительное допущение. Впрочем, парадоксального результата легко избежать, приняв, что ни один коэффициент поглощения не равен единице.
 Практика показала, что
для помещений с небольшим aср (театральные и концертные залы,
учебные аудитории и т. п.) все три формулы дают одинаково удовлетворительный
результат. Для помещений со средними коэффициентами затухания (например,
студии) более близки к измеренным значения времени реверберации, рассчитанные
по формуле Эйринга. Если материалы имеют сильно различающиеся ai, а
сами материалы распределены по поверхностям неравномерно, более близкими к
измеренным получаются значения Т, рассчитанные по формуле Миллингтона.
Используя названные формулы, необходимо принять те a, которые были рассчитаны с
помощью этих же формул при обработке экспериментального материала, полученного
в звукомерной камере.
Практика показала, что
для помещений с небольшим aср (театральные и концертные залы,
учебные аудитории и т. п.) все три формулы дают одинаково удовлетворительный
результат. Для помещений со средними коэффициентами затухания (например,
студии) более близки к измеренным значения времени реверберации, рассчитанные
по формуле Эйринга. Если материалы имеют сильно различающиеся ai, а
сами материалы распределены по поверхностям неравномерно, более близкими к
измеренным получаются значения Т, рассчитанные по формуле Миллингтона.
Используя названные формулы, необходимо принять те a, которые были рассчитаны с
помощью этих же формул при обработке экспериментального материала, полученного
в звукомерной камере.
Определение коэффициента поглощения. Коэффициенты поглощения материалов определяют измерениями в "гулкой" (реверберационной) камере. Обозначим объем камеры через V, а ее время реверберации через TO. После внесения в камеру исследуемого материала с площадью SM время реверберации уменьшается до TM. Тогда:
![]()
Если площадь исследуемого предмета (например, стола, кресла и т. д.) не может быть выражена определенным числом, находят поглощение предмета
![]()
Итак, с помощью вышеприведенных формул Сэбина и Эйринга решают обратную задачу: определяют a или А по измеренному времени реверберации.
Учет
поглощения звука в воздухе. Пауль Сэбин (Paul Sabine) – двоюродный брат У. Сэбина – в
Поглощение
звука вызвано вязкостью и теплопроводностью воздуха, а также молекулярными
потерями. Оно становится заметным на частотах более 2 кГц в помещениях объемом
свыше
![]()
Заменив натуральный логарифм на десятичный, получим формулу с иными числовыми коэффициентами, более удобную для расчетов:
![]()
Коэффициент m
– показатель затухания в воздухе, имеющий размерность м-1, определяют по
графикам, приведенным в руководствах и учебниках по акустике. Он возрастает с
увеличением частоты и уменьшением влажности. Поправка на затухание звука в
воздухе пропорциональна объему, поскольку звуковая энергия ослабляется по всему
пространству помещения. По данным И.Г. Дрейзена в больших студиях уже на
частоте 4 кГц поглощение звука в воздухе достигает 1/3–1/4 общего
звукопоглощения. В помещениях объемом более
Это означает, что время реверберации на верхних частотах в помещениях большого объема определяется климатическими условиями в помещении, т.е. температурой и относительной влажностью.
Оценим на нескольких примерах влияние на время реверберации поглощения звука в воздухе.
Имеется
помещение объемом
![]()
При температуре воздуха 21° и относительной влажности 70, 40 и 20% значения m будут соответственно 0,05; 0,01 и 0,02, а время реверберации – 1,23; 1,05 и 0,84 с, т.е. снижается весьма заметно. Поэтому поддерживать постоянными климатические параметры в студии необходимо не только для того, чтобы исполнители чувствовали себя хорошо, но и чтобы были стабильными акустические условия в студии, другими словами, чтобы частотная характеристика времени реверберации не претерпевала изменений.
Заметим попутно, что вследствие сезонной акклиматизации человеческого организма комфортные условия несколько меняются: летом желательна температура 22–25° при относительной влажности 60–45%, для зимы – 20–23° при относительной влажности 70–50%.
|
|
|
Рис. 4. График влияния энергии диффузного и прямого звука при оценке акустических процессов |
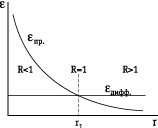
Эффективная (эквивалентная) реверберация. Для более точной оценки акустических процессов в помещении необходимо учитывать энергию и диффузного, и прямого звука (рис.4). На небольших расстояниях от источника преобладает энергия прямого звука, на больших расстояниях – энергия диффузного звука, поскольку первая уменьшается обратно квадрату расстояния, а вторая примерно постоянна. Отношение плотностей этих двух энергий называют акустическим отношением:
![]()
На расстоянии r1 обе составляющие одинаковы (R = 1). На расстояниях более r1 преобладание диффузной энергии проявляется на слух как повышенная “гулкость” помещения. Численное значение r1 связано с объемом помещения V и временем реверберации T эмпирически:
![]()
При объеме
помещения
|
|
|
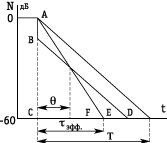
Рис. 5. Различие между временем реверберации Т и временем эффективной реверберации Тэфф. |
На расстояниях более r1 характер звучания определяется главным образом энергией диффузного звука. Для определения времени реверберации в этой области используют ранее приведенные формулы. На близких расстояниях спад уровня имеет иной, более сложный характер, представленный на рис. 5 “ступенчатой” линией А-В-Е. Ощущаемая эффективная реверберация в этом случае будет меньше, чем рассчитанная по ранее приведенным формулам. Сравнивая два процесса спада уровней – со “ступенькой” и без “ступеньки”, Г.А. Голъдберг и С. Ф. Тер-Осипянц обнаружили, что определяющим для равенства двух ощущений длительности процессов является следующее обстоятельство. Два процесса отзвука создают одинаковое впечатление длительности процессов, если через промежуток времени 0,1 - 0,3 с графики обоих процессов проходят через одну точку, соответствующую какому-то значению уровня. Время эффективной реверберации Tэфф. < Т определяют на основе равенства площадей двух треугольников В-С-Е и А-С-F. Оно характеризуется временем, в течение которого уровень уменьшился бы на 60 дБ от начального уровня 0 дБ при условии спада уровня без “ступеньки”, и зависит от соотношения энергий диффузного и прямого звука, численно выражаемого акустическим отношением R и коэффициентом направленности микрофона W (если в качестве приемника звука выступает микрофон). Для расчета времени эффективной реверберации была предложена формула
![]()
В этой формуле Q – ранее указанный промежуток времени, в течение которого слух достаточно хорошо интегрирует процесс спада уровня, его среднее значение 0,2 с, что несколько больше постоянной времени слуха t = 0,165 с. Подставив в формулу численное значение 6Q, получим
![]()
В качестве примеров рассчитаем Tэфф. при Т = 2 с, R = 1, для
W = 1 (ненаправленный микрофон) и W = 3 (микрофон с косинусоидальной или кардиоидной диаграммой направленности):
![]()
![]()
Изменяя расстояние между источником звука и используя микрофоны с разными диаграммами направленности, можно в широких пределах регулировать время эффективной реверберации. Тем самым подбирают эффект реверберации в соответствии с содержанием передаваемых сцен или с жанром музыкальных произведений.
Из-за различного расстояния от инструментов оркестра до микрофона может возникнуть нежелательный эффект, нарушающий баланс звучания (под балансом понимают задуманную композитором определенную соразмерность звучностей различных оркестровых групп, солирующего инструмента и оркестрового сопровождения). Ближайшие к микрофону инструменты будут воздействовать на него прямым звуком, а удаленные – звуком с заметной реверберацией. Перемещение певца-солиста во время исполнения перед микрофоном приведет к ощущению изменения “гулкости” помещения.
Понимая явление эффективной реверберации и используя его, можно добиться полезного эстетического воздействия. Так, на общем фоне звучания оркестра с присущей данному помещению реверберацией передавать звучание солистов с укороченным временем реверберации, улучшая тем самым разборчивость пения или добиваясь четкого звучания солирующего инструмента, например рояля. На основе этого же явления студию с большим временем реверберации можно успешно использовать для небольших ансамблей с малой эффективной реверберацией, необходимой для них.
Реверберация с позиций слушателя и исполнителя. Рассмотрим, насколько правомерно при проектировании залов требование диффузности звукового поля, положенное в основу статистической теории.
При акустическом проектировании концертных и театральных залов выполнение требования диффузности поля и вытекающего из него требования равномерного распределения звукопоглощающих материалов по всем преградам приведет к тому, что значительная часть звуковой энергии будет бесцельно теряться. Тем самым пренебрегают интересами и слушателей, и исполнителя. Последний должен хорошо слышать себя и своих товарищей по ансамблю. Для этого необходимо, чтобы достаточно большое количество отраженной звуковой энергии возвращалось к исполнителю. Это тем более важно потому, что тесно расположенные в группе исполнители сами по себе поглощают значительную долю энергии, а значит в зоне их расположения дополнительное звукопоглощение должно быть сравнительно небольшим.
Оценить комфортность условий исполнения для певца можно на основании данных, приведенных в табл. 1.
 Несколько меньшие
значения времени реверберации являются комфортными для чтеца. Однако с позиций
слушателя более приемлемо время реверберации от 1 до 1,7 с в зависимости от
характера исполняемого произведения. Чтобы разрешить это противоречие,
необходимо создать достаточно большую местную реверберацию в зоне расположения
исполнителей. Эффективные звукопоглощающие материалы надо размещать на тех
поверхностях, которые могут дать интенсивные отражения с большой разностью хода
по отношению к прямому звуку. Остальные преграды покрывают звукопоглощающими
материалами лишь в той мере, чтобы обеспечить нужную реверберацию в зале и не
допустить неравномерного затухания разных частотных составляющих спектра звука.
Несколько меньшие
значения времени реверберации являются комфортными для чтеца. Однако с позиций
слушателя более приемлемо время реверберации от 1 до 1,7 с в зависимости от
характера исполняемого произведения. Чтобы разрешить это противоречие,
необходимо создать достаточно большую местную реверберацию в зоне расположения
исполнителей. Эффективные звукопоглощающие материалы надо размещать на тех
поверхностях, которые могут дать интенсивные отражения с большой разностью хода
по отношению к прямому звуку. Остальные преграды покрывают звукопоглощающими
материалами лишь в той мере, чтобы обеспечить нужную реверберацию в зале и не
допустить неравномерного затухания разных частотных составляющих спектра звука.
Даже при проектировании студий следует относиться осмотрительно к рекомендации равномерно размещать звукопоглощающие материалы. В зоне расположения исполнителей желательно обеспечить большую реверберацию, чем в остальной части студии. Правда, при этом руководитель записи или передачи несколько скован в возможностях иного размещения ансамбля, например, выигрышного со зрелищных позиций, что имеет место при телевизионном вещании.
Слуховое ощущение реверберации. Не вся длительность процесса реверберации ощущается нашим слухом. Постоянная времени слуха t, характеризующая инерционные свойства слуха и соответствующая спаду слухового ощущения в е раз (уменьшению уровня громкости на 8,7 дБ), составляет по разным данным 0,125–0,15 с (по некоторым сведениям даже 0,165 с). Это соответствует спаду уровня интенсивности на 60 дБ, т.е. времени стандартной реверберации 0,86–1,05 с. Следовательно, процесс реверберации при Т < 0,86 с мало заметен на слух ввиду его маскировки собственным процессом спада слухового ощущения. Еще более он маскируется акустическими помехами (шумами) помещения. Поэтому длительность слышимой части отзвука составляет менее половины времени реверберации и реверберация при Т < 0,86 с мало ощущается нашим сознанием. Для ощущения полноты музыки время реверберации должно быть существенно больше 0,86 с. Как известно, этот оптимум составляет для различных музыкальных звучаний от 1 до 1,7 с.
Ограничения теории по диапазону частот и объему помещения. Рассмотрим ограничения на использование расчетов, основанных на статистической теории, по диапазону частот и объемам помещений.
Частотный
диапазон слышимых звуков простирается от 20 до 20 000 Гц. Между тем
акустические расчеты проводятся для интервала, ограниченного частотами 100–4000
Гц. Причина ограничения по верхним частотам очевидна из предыдущего. На
частотах более 4 кГц в помещениях большого объема трудно разделить составляющие
поглощения, обусловленные материалами и воздухом. Поэтому достоверные данные о
коэффициентах поглощения материалов на более высоких частотах отсутствуют. Так
же трудно, если не невозможно вовсе, получить достоверные данные о
коэффициентах поглощения на частотах ниже 100 Гц. Линейные размеры образцов
материалов должны быть, по крайней мере, соизмеримы с длиной волны. Для частоты
100 Гц это
Нижний предел применения статистических методов по объему помещения обусловлен тем, что при размерах преград, соизмеримых с длиной волн, невозможно пользоваться понятием отражения волн.
Для оценки нижней границы по объему пользуются соотношением
![]()
Обоснование причины ограничения применимости статистических методов в помещениях большого объема требует более подробного объяснения. Предпосылки статистической теории тем ближе к действительности, чем большее количество отражений претерпевает звуковая энергия по мере затухания. Отсюда следует, что положения статистической теории не применимы к крупным помещениям и к помещениям с большим средним коэффициентом поглощения. В обоих случаях количество отражений оказывается слишком малым. Рассмотрим некоторые конкретные случаи.
1.
В помещении
объемом 12 х 9 х
2.
Для зала с
линейными размерами 40, 30,
3.
Пусть
комната имеет размеры 6, 4 и
Из этих примеров видно, насколько формулы, по которым определяют время реверберации, основываются в некоторых случаях на спорных положениях.
В статистической теории не рассматриваются соотношение между энергией прямого и диффузного звука, энергия начальных, сравнительно редких отражений, направленные потоки энергии, фокусировка звука. Сфера ее рассмотрения – достаточно плотный временной ряд отражений, создающий слитную последовательность запаздывающих звуков. Ее выводы тем точнее, чем дальше находится точка наблюдения от точки расположения источника звука.
Статистическая теория имеет ряд уязвимых мест. Некоторые ее положения не находят подтверждения в повседневной практике, расходятся с ней. Она не объясняет акустических процессов на очень низких и очень высоких звуковых частотах, в небольших и очень больших помещениях, в помещениях с резким преобладанием какого-то линейного размера, с неравномерным распределением звукопоглощающих материалов.
Несмотря на это, она является мощным и действенным инструментом исследования и проектирования помещений, поскольку дает числовые значения параметров, характеризующих акустику помещений. Важно знать ее сильные и слабые стороны, с пониманием и осторожностью применять расчетные формулы и на этой основе сознательно пользоваться ее достижениями.
Волновая теория
Основные положения. В статистической теории отзвук рассматривается как затухание последовательного ряда отраженных звуковых импульсов, излученных источником звука. Подразумевается, что форма импульсов, следовательно, и их спектр, заданные источником звука, при отражениях остаются неизменными. Такое представление вызвало сомнения принципиального характера: ведь замкнутый воздушный объем помещения, если его размеры соизмеримы с длиной волны или больше ее, следует рассматривать как колебательную систему с распределенными параметрами, которая обладает спектром собственных (резонансных) частот. После прекращения действия источника звука, поддерживающего вынужденные колебания воздуха в помещении, в системе совершаются только собственные колебания, они затухают по мере поглощения энергии. В явлении реверберации нет места остаточному колебательному процессу, навязанному ранее действием вынуждающей внешней силы; отзвук есть собственное затухающее колебание воздушного объема с частотами, зависящими от размеров и формы помещения.
Следовательно, сутью реверберации являются не многократные отражения, а постепенно затухающие собственные колебания объемного резонатора, не зависящие от внешних влияний.
Такой взгляд положен в основу волновой теории акустических процессов в помещении.
Акустику помещений с позиции волновых, колебательных процессов анализировали Дж. В. Стретт, Бейль, Курант, Шустер и Ветцман, Кнудсен, Морз и Болт и другие. Среди разработчиков волновой теории в нашей стране следует в первую очередь назвать И.Г. Дрейзена и В.В. Фурдуева.
Большинство инженеров полагают, что волновая теория основана на анализе действия объемных электромагнитных резонаторов. Действительно, в обеих теориях есть много общего, включая расчетные соотношения. Но волновую теорию реверберации начали разрабатывать еще в середине прошлого века, значительно раньше статистической. Просто в ее разработке продвинулись меньше, чем в статистической.
Идеи,
положенные в основу волновой теории, были впервые высказаны Дж. В. Стреттом
(лордом Релеем). В “Основах акустики”, изданных впервые в
![]()
Отсюда
![]()
В приведенных выражениях l, b, h – линейные размеры, р, q, n – любые целые числа. В зависимости от значений коэффициентов р, q, n принята следующая классификация типов образующихся стоячих волн:
· осевые, когда два из трех коэффициентов равны нулю,
· касательные, когда один из коэффициентов равен нулю,
· косые, когда ни один из коэффициентов не равен нулю.
Осевые волны отражаются только от одной пары противоположных параллельных преград (стен), касательные – от двух пар (т.е. устанавливаются в плоскости, параллельной третьей паре преград), косые – от всех пар преград. Для многих материалов коэффициенты поглощения зависят от угла падения волны на преграду. В связи с этим волны разных типов затухают с разной скоростью. Затухание получается наибольшим для косых волн и наименьшим для осевых. Поэтому, когда источник звука возбуждает колебания разных типов, то различные собственные колебания, даже с близкими частотами, будут затухать с неодинаковой скоростью. В результате кривая спада интенсивности звука не будет иметь регулярного вида, который предписывается статистической теорией. Крутизна спада уровня на разных стадиях отзвука будет различной, и тогда теряется определенный смысл самого понятия времени реверберации. Процесс спада будет складываться из разных частных процессов и значит не будет изображаться экспоненциальной кривой (см. рис. 1а статьи, опубликованной в предыдущем номере), а будет следовать ей лишь в среднем. На него будут накладываться небольшие флуктуации, изображенные на рис. 2 (см. там же) штриховой линией. Практика показывает, что наличие малых флуктуаций благоприятно сказывается на оценке качества звучания. Поэтому значение статистической теории не только не снижается, а, наоборот, приобретает новую опору в выводах волновой теории. Итак, в статистической теории ход спада интенсивности рассчитывается методами теории вероятности, “в среднем”, а флуктуации фактического спада относительно усредненной формы определяются методами волновой теории.
Из волновой теории вытекает, что помещения простой правильной геометрической формы менее удовлетворяют условию диффузности поля, чем помещения сложной геометрической формы с непараллельными стенами, косо поставленными плоскостями или выпуклыми поверхностями, углублениями в виде кессонов. Разумеется, линейные размеры этих поверхностей должны быть соизмеримы с длиной волны или быть больше ее.
Спектр
собственных частот. Приведем в качестве примеров результаты расчета длин волн и
частот, соответствующих резонансным колебаниям в помещении в виде
прямоугольного параллелепипеда с линейными размерами 10, 6,
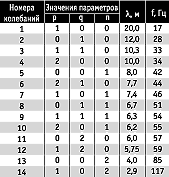 Из результатов расчета
видно, что на нижних частотах резонансы следуют через значительные промежутки и
должны привести к заметному изменению спектра отзвука по сравнению со спектром
исходного звучания, следовательно, к изменению тембра отзвука. Между тем,
повседневный опыт убеждает нас в обратном. Как объяснить это противоречие?
Объяснение сводится к следующему. В той области частот, где резонансные частоты
расположены редко, соответствующие частотные составляющие в спектре речевых и музыкальных
сигналов почти не встречаются. Реальное значение могли бы иметь, например, 13 и
14 частоты, но интенсивность резонансных колебаний столь больших номеров
невелика, поэтому заметного изменения тембра отзвука не произойдет. С
увеличением частоты плотность резонансных частот быстро возрастает. Так, в
области 500 Гц на 1 Гц полосы частот придется примерно 10 резонансных частот. В
связи с этим в помещениях большого объема, какими являются концертные и
театральные залы, ухудшения звучания не происходит.
Из результатов расчета
видно, что на нижних частотах резонансы следуют через значительные промежутки и
должны привести к заметному изменению спектра отзвука по сравнению со спектром
исходного звучания, следовательно, к изменению тембра отзвука. Между тем,
повседневный опыт убеждает нас в обратном. Как объяснить это противоречие?
Объяснение сводится к следующему. В той области частот, где резонансные частоты
расположены редко, соответствующие частотные составляющие в спектре речевых и музыкальных
сигналов почти не встречаются. Реальное значение могли бы иметь, например, 13 и
14 частоты, но интенсивность резонансных колебаний столь больших номеров
невелика, поэтому заметного изменения тембра отзвука не произойдет. С
увеличением частоты плотность резонансных частот быстро возрастает. Так, в
области 500 Гц на 1 Гц полосы частот придется примерно 10 резонансных частот. В
связи с этим в помещениях большого объема, какими являются концертные и
театральные залы, ухудшения звучания не происходит.
Иное положение складывается в помещениях небольшого объема, например в речевых (дикторских) студиях и жилых комнатах. Известны жалобы дикторов, что их голос в речевых студиях звучит совершенно необычно, неприятно, ощущается “бубнение”. Объясняется это тем, что в помещениях небольшого объема основная резонансная частота попадает в область хорошо слышимых звуков. Для борьбы с этим неприятным явлением приходится либо значительно уменьшать время реверберации путем использования в студии эффективно поглощающих материалов, либо ограничивать полосу пропускания электрического тракта ниже 250–300 Гц. “Бубнение” свойственно и многим жилым комнатам. Устранить этот недостаток почти невозможно, так как нет дешевых материалов, эффективно поглощающих звуковую энергию в области 100 Гц и ниже.
Особенно выражены резонансы в помещениях с совпадающими линейными размерами. В этом случае совпадают резонансные частоты, обусловленные стоячими волнами в разных плоскостях. Наихудшим в акустическом отношении является помещение кубической формы, наилучшим – помещение, пропорции которого приближаются к “золотому сечению”. Заключение, сделанное акустиками древности, нашло подтверждение в выводах волновой теории.
Дж. В. Стретт в “Теории звука” отметил наблюдавшееся им вырождение спектра собственных частот в помещении с преобладанием одного из линейных размеров и, следовательно, с преобладанием одного из видов собственных колебаний: “В моем доме есть подземный коридор, в котором можно, пропев надлежащую ноту, возбудить свободные колебания, продолжающиеся много секунд, и часто случается, что звучащая нота сопровождается отчетливыми биениями.” Эти биения порождаются одновременным возбуждением двух близких собственных частот.
Каждый человек обнаружит резонансные частоты помещения, пропев несколько звуков разной частоты. Помещение отзовется на некоторые из них усилением колебаний.
Убедиться, что помещение небольшого объема с совпадающими линейными размерами обладает обедненным спектром собственных частот, можно, проделав простой опыт. В слабо заглушенном помещении (например, ванной комнате), стены которого покрыты кафельными плитками, ударьте в ладоши. Вместо ожидаемого шумового отклика вы услышите звенящий звук с заметно выраженной высотой тона. Это объясняется бедностью спектра собственных частот такого помещения.
Стретт заметил, что люди с особо развитым слухом, например слепые, обладают способностью решить обратную задачу: анализируя каким-то неведомым способом спектр отзвука, они определяют линейные размеры помещения и их пропорции.
Коэффициент поглощения с позиций волновой теории. Волновая теория дала ответ на вопрос, имеющий практическое значение при сооружении различных залов и аудиторий: почему звукопоглощающие материалы, коэффициенты поглощения которых определены в звукомерной камере, ведут себя в помещении иным образом, как будто их коэффициенты поглощения отличаются от измеренных и указанных в справочниках.
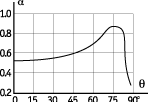
В звукомерной камере материал, как правило, исследуют в диффузном поле. Коэффициент поглощения определяется усреднением по всем углам падения звуковых волн, интегрально. Но коэффициент поглощения многих материалов зависит от угла падения волны. Поэтому поглощение материала в зале даже на близких частотах будет зависеть от типа волны – осевого, касательного, косого. А от образующегося типа волны зависят углы, под которыми волны падают на преграду. Для большинства пористых материалов коэффициент поглощения растет с увеличением угла падения по закону a(q) = a(0)/cos(q), где a(0) – коэффициент поглощения при нормальном (перпендикулярном) падении, а q– угол между нормалью и направлением падающей на преграду волны. Но при приближении q к 90° a резко уменьшается в результате скольжения волны вдоль преграды (рис. 6). Поэтому в помещении материал ведет себя иначе, чем в звукомерной камере.
|
|
|
Рис. 6. Зависимость коэффициента поглощения a пористого материала от угла падения звуковой волны |
Кроме того, из-за нестационарности звукового поля a зависит не только от свойств материала преграды, но и от общего поглощения помещения A = acpS. Поэтому коэффициент поглощения одного и того же материала в разных помещениях может отличаться в 1,5–2 раза. Правда, учитывая, что оптимум времени реверберации – понятие несколько неопределенное и что расчеты времени реверберации в силу высказанных ранее причин носят приближенный характер, с такими тонкостями поведения звукопоглощающих материалов чаще всего не считаются.
Противоположность и единство теорий. При всей разнице в подходах к объяснению акустических процессов в помещениях статистическая и волновая теории дополняют друг друга и потому в известной мере работают на практику совместно.
В заключение настоящего раздела заметим следующее. Многие люди, попав в помещение с большой реверберацией, произносят: “ Какой здесь резонанс!” Известный акустик В. Кнудсен высказался по этому поводу: “Те, кто смешивают процесс реверберации с резонансом, видимо, не так уж далеки от истины.” Кнудсен этим высказыванием подчеркнул физическое единство акустических процессов, описываемых с разных точек зрения статистической и волновой теориями.
Принципиальное различие подходов к объяснению акустических процессов заключается в том, что в одном случае процесс отзвука рассматривается с помощью теории вероятностей усредненно, а в другом с волновых позиций определяются отклонения фактического хода процесса от “среднего”.
Из оптики известно, что при уменьшении длины волны волновые законы приближаются к законам геометрической оптики. Точно так же в помещениях, размеры которых весьма велики по сравнению с длиной волны, можно пользоваться законами геометрической оптики, строить пути звуковых лучей, находить точки фокусов, определять запаздывание начальных отражений, т.е. использовать весь арсенал геометрической теории.
Геометрическая (лучевая) теория
Основные положения. Геометрическая (лучевая) теория акустических процессов в помещениях основана на законах геометрической оптики. Движение звуковых волн рассматривают подобно движению световых лучей. В соответствии с законами геометрической оптики при отражении от зеркальных поверхностей угол отражения b равен углу падения a, и падающий и отраженный лучи лежат в одной плоскости. Это справедливо, если размеры отражающих поверхностей много больше длины волны, а размеры неровностей поверхностей много меньше длины волны.
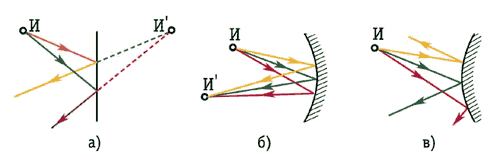
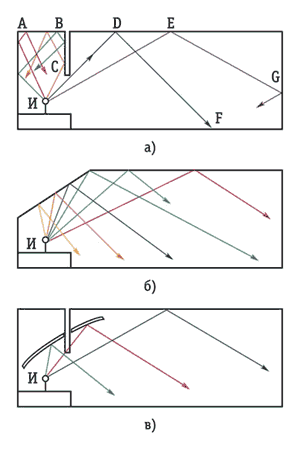
Характер отражения зависит от формы отражающей поверхности. При отражении от плоской поверхности (рис.7, а) возникает мнимый источник И', место которого ощущается на слух подобно тому, как глаз видит мнимый источник света в зеркале. Отражение от вогнутой поверхности (рис.7, б) приводит к фокусировке лучей в точке И'. Выпуклые поверхности (колонны, пилястры, крупные лепные украшения, люстры) рассеивают звук (рис.7, в).
Роль начальных отражений. Немаловажным для слухового восприятия является запаздывание отраженных звуковых волн. Звук, излученный источником, доходит до преграды (например, стены) и отражается от нее. Процесс многократно повторяется с потерей при каждом отражении части энергии. На места слушателей (или в точку расположения микрофона) первые запаздывающее импульсы, как правило, приходят после отражения от потолка и стен зала (студии).
Вследствие
инерционности слуха человек обладает способностью сохранять (интегрировать)
слуховые ощущения, объединять их в общее впечатление, если они длятся не более
50 мс (точнее 48 мс). Поэтому к полезному звуку, подкрепляющему исходный,
относятся все волны, которые достигают уха в течение 50 мс после исходного звука.
Запаздыванию на 50 мс соответствует разница в пути
Исследования начальных отражений методом акустического моделирования были проведены в Научно-исследовательском кинофотоинституте (НИКФИ) под руководством А. И. Качеровича. Изучалось влияние на качество звучания речи и музыки формы, объема, линейных размеров, размещения звукопоглощающих материалов. Получены интересные результаты.
Существенную роль играет направление прихода начальных отражений. Если запаздывающие сигналы, т.е. все ранние отражения, поступают к слушателю с того же направления, что и прямой сигнал, слух почти не различает разницы в качестве звучания по сравнению со звучанием только прямого звука. Возникает впечатление "плоского" звука, лишенного объемности. Между тем даже приход только трех запаздывающих сигналов по разным направлениям, несмотря на отсутствие реверберационного процесса, создает эффект пространственного звучания. Качество звучания зависит от того, с каких направлений и в какой последовательности приходят запаздывающие звуки. Если первое отражение поступает с фронтальной стороны, звучание ухудшается, а если с тыльной стороны, то резко ухудшается.
Весьма существенно время запаздывания начальных отражений по отношению к моменту прихода прямого звука и относительно друг друга. Длительности запаздывания должны быть различными для наилучшего звучания речи и музыки. Хорошая разборчивость речи достигается, если первый запаздывающий сигнал поступает не позже 10 - 15 мс после прямого, а все три должны занимать интервал времени 25 - 35 мс. При звучании музыки наилучшее ощущение пространственности и "прозрачности" достигается, если первое отражение приходит к слушателю не ранее 20 мс и не позже 30 мс после прямого сигнала. Все три запаздывающих сигнала должны располагаться в промежутке времени 45 - 70 мс. Наилучший пространственный эффект достигается, если уровни запаздывающих начальных сигналов незначительно отличаются друг от друга и от уровня прямого сигнала.
При подключении к структуре начальных отражений (первого, второго, третьего) остальной части отзвука наиболее благоприятное звучание получается в том случае, когда вторая часть процесса начинается после всех дискретных отражений. Подключение же процесса реверберации (отзвука) сразу же за прямым сигналом ухудшает качество звучания.
При обеспечении оптимальной структуры начальных (ранних) отражений звучание музыки остается хорошим даже при значительном (на 10 - 15%) отклонении времени реверберации от рекомендуемого. Достижение оптимального запаздывания отраженных сигналов по отношению к прямому звуку выдвигает требование к минимальному объему помещения, которое не рекомендуется нарушать. Между тем при проектировании помещения выбирают его размеры, исходя из заданной вместимости, т.е. решают задачу чисто экономически, что неправильно. Даже в небольшом концертном зале оптимальную структуру ранних отражений можно получить лишь при заданных высоте и ширине зала перед эстрадой, меньше которых спускаться нельзя. Известно, например, что звучание симфонического оркестра в зале с низким потолком существенно хуже, чем в зале с высоким потолком.
 Полученные результаты
дали возможность выработать рекомендации в отношении времени запаздывания и
размеров зала. Учитывалось, что первый запаздывающий сигнал, как правило,
приходит от потолка, второй - от боковых стен, третий - от задней стены зала.
Разные требования по времени задержки начальных отражений объясняются
особенностями речи и музыкальных звуков и различием решаемых акустических задач
(табл.3).
Полученные результаты
дали возможность выработать рекомендации в отношении времени запаздывания и
размеров зала. Учитывалось, что первый запаздывающий сигнал, как правило,
приходит от потолка, второй - от боковых стен, третий - от задней стены зала.
Разные требования по времени задержки начальных отражений объясняются
особенностями речи и музыкальных звуков и различием решаемых акустических задач
(табл.3).
Чтобы
добиться хорошей разборчивости речи, запаздывания должны быть сравнительно
небольшими. При звучании музыки нужно подчеркнуть мелодическое начало, для
обеспечения слитности звуков необходимо большее время запаздывания начальных
отражений. Отсюда вытекают рекомендуемые размеры концертных залов: высота и
ширина не менее 9 и
Увеличивать
высоту и ширину зала в некоторой мере можно лишь на расстоянии от портала сцены
(эстрады), превышающем примерно 1/4 - 1/3 общей длины зала: высоту до
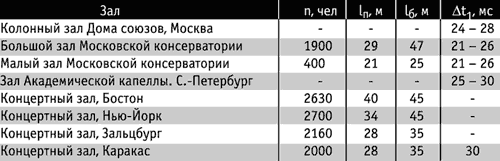
В табл. 4 приводим сведения о геометрии некоторых залов, акустические качества которых считаются хорошими (n - вместимость зала, lп - наибольшее удаление слушателя от эстрады в партере, lб - то же на балконе, Dt1 - время запаздывания первого отражения).
Таким образом, минимальные размеры помещения для воспроизведения музыки (высота и ширина) не связаны с его вместимостью, а определяются необходимой структурой начальных отражений. Даже если помещение предназначено для исполнения музыки в отсутствии слушателей (студия звукозаписи, звукового вещания, ателье записи музыки, зал прослушивания киностудии), его размеры должны определяться только качеством звучания музыки. "Экономить" на этих размерах - значительно ухудшать качество звучания.
Исторические примеры. По сохранившимся до наших времен культовым и зрелищным сооружениям видно, что основные положения лучевой теории были известны древним строителям и что эти положения неукоснительно соблюдались. Размеры греческих и римских театров на открытом воздухе были выбраны такими, чтобы в наибольшей степени использовать энергию отраженных волн.
Театры
(рис.8) содержали три основные части:
·
сцену
(shena) глубиной 3,5 -
· площадку перед сценой - орхестру (orhestra буквально "место плясок"), на которой располагался хор и выступали танцоры;
· поднимающиеся ступенями зрительские места вокруг орхестры, образующие так называемый амфитеатр (от греческих слов amphi - "с обеих сторон", "кругом" и theatron - "место зрелищ").
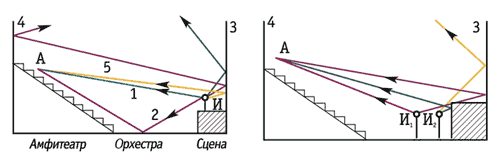
Звуки от
исполнителей достигали зрителей, располагавшихся на амфитеатре, прямым путем 1,
а также после отражений от поверхности орхестры (луч 2) и стены 3, находящихся
позади сцены (рис.9,а). Плоскость орхестры покрывали хорошо отражающим
материалом. Как указывал Витрувий, высоту стены 3 следовало выбирать равной
высоте парапета 4, ограждавшего верхний ряд амфитеатра, "для улучшения
акустики". Видимо, речь шла о том, чтобы не допустить излишнего рассеяния
звуковой энергии в пространстве. Глубину сцены в греческих театрах делали
небольшой, чтобы лучи 5, отраженные от задней стены, не слишком запаздывали по
отношению к прямому лучу 1 и не ухудшали разборчивость речи актеров. Часть
звуковой энергии, отразившись от стен 3 и 4, уходила вверх. В современных
крытых театральных залах эта энергия отражается потолком вниз и увеличивает
интенсивность звука на зрительских местах. На орхестре происходили танцы и
располагался хор, повторявший реплики актеров, т.е. выполнявший задачу
звукоусиления. При расположении хора в точке 1 звуковые лучи, отразившись от
стены 3 (рис.9,б), приходят к зрителю с большой задержкой во времени,
вызывающей эхо. Для уменьшения этого недостатка в римских театрах хор стали
располагать ближе к сцене, в точке 2. Тогда для направления энергии в сторону
зрителей начали использовать отражения от сцены (ее высота в римских театрах
достигала
Особую роль в усилении и обогащении звучания играли так называемые "гармоники" - системы резонаторов в виде бронзовых цилиндрических сосудов и глиняных кувшинов-амфор. Они располагались в нишах стены позади зрительских мест и под скамьями. Греки считали, что для благозвучия речи и музыки резонаторы должны быть подобраны или настроены по тонам музыкальных гамм: энгармонической, хроматической и диатонической.
· Первая система, по мнению их создателей, придавала звукам торжественность и строгость;
· Вторая, благодаря "толпящимся" нотам, - утонченность, нежность звучанию;
· Третья - из-за консонансности интервалов - естественность музыкальному исполнению.
Очевидно, что античные архитекторы при строительстве театров искали и находили технические пути передачи зрителям и слушателям не только смысловой (семантической), но и художественной (эстетической) информации, стремились обогатить музыкальное звучание.
Рациональной формой и разумно выбранными размерами отличались театральные и концертные залы 18 и 19 веков. Ряд хороших в акустическом отношении театральных и концертных залов был построен в разных странах в 20 веке.
 Неудачные решения.
Казалось бы, опыт, накопленный за тысячелетия, должен использоваться
современными архитекторами и строителями. Между тем множатся примеры
неудовлетворительных акустических решений, например, строительство залов
круглой или эллиптической в плане формы (кинотеатр "Колизей" в
Санкт-Петербурге, концертный зал им. Чайковского в Москве и др.). В них
образуются зоны фокусировки отраженных лучей и зоны, в которые отраженные лучи
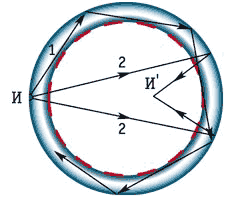
либо не попадают, либо попадают с большой временной задержкой. В круглом в
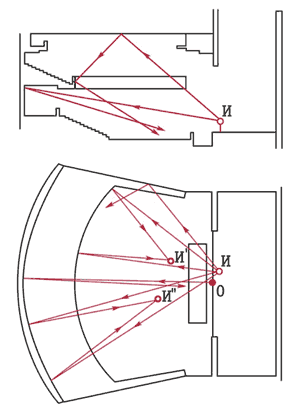
плане зале (рис.10) касательный к стене луч 1 и при последующих отражениях
остается в близкой к стене зоне. Лучи 2, распространяющиеся примерно в
диаметральном направлении, образуют после отражения мнимое изображение
источника И', в котором интенсивность звука, как и в кольцевой зоне возле
стены, повышена. Неудовлетворительными являются залы с плоским потолком и
низким порталом сцены (рис.11, а). Зона АВС оказывается своеобразной ловушкой
для значительной части, излучаемой источником звука энергии. Только зона DE
дает полезные отражения, но они попадают лишь в удаленную часть зала ЕС.
Предпочтительнее конструкции с рассеивающим потолком (рис.11,б), акустической
раковиной и козырьком (рис.11,в).
Неудачные решения.
Казалось бы, опыт, накопленный за тысячелетия, должен использоваться
современными архитекторами и строителями. Между тем множатся примеры
неудовлетворительных акустических решений, например, строительство залов
круглой или эллиптической в плане формы (кинотеатр "Колизей" в
Санкт-Петербурге, концертный зал им. Чайковского в Москве и др.). В них
образуются зоны фокусировки отраженных лучей и зоны, в которые отраженные лучи
либо не попадают, либо попадают с большой временной задержкой. В круглом в
плане зале (рис.10) касательный к стене луч 1 и при последующих отражениях
остается в близкой к стене зоне. Лучи 2, распространяющиеся примерно в
диаметральном направлении, образуют после отражения мнимое изображение
источника И', в котором интенсивность звука, как и в кольцевой зоне возле
стены, повышена. Неудовлетворительными являются залы с плоским потолком и
низким порталом сцены (рис.11, а). Зона АВС оказывается своеобразной ловушкой
для значительной части, излучаемой источником звука энергии. Только зона DE
дает полезные отражения, но они попадают лишь в удаленную часть зала ЕС.
Предпочтительнее конструкции с рассеивающим потолком (рис.11,б), акустической
раковиной и козырьком (рис.11,в).
 Неудовлетворительным в
акустическом отношении являлся знаменитый зал Альберт-холл в Лондоне шириной
Неудовлетворительным в
акустическом отношении являлся знаменитый зал Альберт-холл в Лондоне шириной
Примером
неудачного акустического решения может служить Большой зал Центрального театра
Российской армии (ЦТРА). Основные недостатки зала: большая ширина, равная в
середине зала
Когда-то хорошей акустикой отличался актовый зал МТУСИ, где даже проводились симфонические концерты, транслировавшиеся по радио. Акустические условия значительно ухудшились после косметического ремонта зала. Была изменена конструкция ограждения балкона, в глубине которого был поставлен отражающий щит. Сильные отражения от парапета и щита ухудшили звучание в партере. Из-за больших запаздываний снизилась разборчивость речи.
 Примером неудачного
акустического решения является и Центральный концертный зал гостиницы
"Россия" в Москве. Квадратная в плане форма зала привела к обеднению
спектра собственных частот, низкий потолок создает малую задержку первых
отражений, а большая ширина зала приводит к тому, что отражения от стен не
попадают в первую половину партера. Трижды пытались улучшить звучание заменой
звукопоглощающих материалов и их размещением в зале. Однако скомпенсировать
заведомо неудачную исходную форму зала не удалось.
Примером неудачного
акустического решения является и Центральный концертный зал гостиницы
"Россия" в Москве. Квадратная в плане форма зала привела к обеднению
спектра собственных частот, низкий потолок создает малую задержку первых
отражений, а большая ширина зала приводит к тому, что отражения от стен не
попадают в первую половину партера. Трижды пытались улучшить звучание заменой
звукопоглощающих материалов и их размещением в зале. Однако скомпенсировать
заведомо неудачную исходную форму зала не удалось.
Даже в
помещениях с правильно выбранными формой и линейными размерами, пропорции
которых приближаются к "золотому сечению", обнаруживаются недостатки
звучания, устранение которых занимает много времени, сил и средств. В
тщательной подготовке к нормальной эксплуатации нуждаются студии звукового и
телевизионного вещания. Примером может служить комплекс работ по подготовке
студии N5 Государственного дома радиовещания и звукозаписи (ГДРЗ). Студия
предназначена для исполнения произведений крупных форм с участием
симфонического оркестра и хора в присутствии слушателей. Ее линейные размеры
(29,8 х 20,5 х
Встречаются залы, рассчитанные на небольшое количество слушателей, соответственно небольшой площади и невысокие. Авторы их, по-видимому, полагали, что при небольших размерах зала "все будет хорошо слышно". В действительности в таких залах на слушательских местах образуется плотная структура начальных отражений. Из-за этого при небольшом времени реверберации звучание оказывается "плоским", подобно звучанию на открытом воздухе, а при большом времени реверберации теряется "прозрачность" звучания, начинается маскировка последующих музыкальных звуков предыдущими.
Также неудовлетворительны большей частью так называемые актовые залы. Они предназначаются для собраний, т.е. для звучания речи. Низкий потолок, гладкие параллельные стены, лишенные акустической отделки порождают неоптимальные начальныфяе отражения. Попытки проводить в них концерты не приносят успеха. Музыка звучит в них плохо. Хуже всего, что концерты в таких залах портят публику. Ниже всякой критики акустика так называемых "концертно-спортивных" залов.
В нашей стране большой вред качеству театральных и концертных залов принесла "борьба с архитектурными излишествами". "Излишествами" были объявлены все звукорассеивающие и звукопоглощающие конструкции и даже мягкая обивка кресел, призванная служить эквивалентом отсутствующих зрителей. В результате - на слушательских местах плохая структура начальных отражений, невысокая диффузность, а при частичном заполнении - чрезмерная "гулкость".
Лучшие залы. Непревзойденными по качеству звучания остаются Колонный зал Дома союзов, Большой и Малый залы Московской консерватории, Большой зал Санкт-Петербургской филармонии и некоторые другие залы старой постройки.
К достижениям отечественной архитектурной акустики следует отнести зрительные залы Детского музыкального театра, Театра им. Евг. Вахтангова, Московского драматического театра им. А.С. Пушкина, Дворца культуры ЗиЛ, студии Государственного дома звукозаписи, ателье записи звука и зал прослушивания "Мосфильма". При их проектировании и строительстве были учтены положения и рекомендации отечественных и зарубежных акустиков.
В этих залах соблюдены требования геометрической акустики: рационально выбраны форма и размеры, что обеспечило высокую степень диффузности поля и оптимизацию времен запаздывания начальных отражений. В каждом конкретном случае выбраны свои архитектурно-планировочные решения. Залам сравнительно небольшой ширины придана форма прямоугольного параллелепипеда. Таковы Большой и Малый залы Московской консерватории, Большой зал московского Дома ученых. При небольшой ширине количество отражений, приходящих на места слушателей, быстро нарастает со временем и в завершающей части процесса реверберации настолько велико, что обеспечивает хорошую диффузность поля. В залах большой ширины (Колонный зал Дома союзов, Большой зал Санкт-Петербургской филармонии) введены звукорассеивающие конструкции в виде ряда колонн. В современных залах большой вместимости хорошего рассеяния звуков достигают членением стен и потолка и установкой крупных рассеивающих поверхностей на стенах.
Важное значение имеет материал, которым отделаны стены и потолок. Наилучшим является дерево. Звучание музыки в залах, отделанных деревом, отличается красивой тембральной окраской. Наоборот, совершенно противопоказаны железобетонные конструкции, особенно тонкие, и штукатурка по сетке рабица. Звуки, отраженные от этих поверхностей, обладают неприятным "металлическим" оттенком.
Заключение
Три рассмотренные теории с разных сторон объясняют акустические процессы, происходящие в помещениях. Из них только одна - статистическая - позволяет определить численно важную величину, характеризующую акустические свойства помещения - время реверберации. Следует лишь сознательно, критически относиться к получаемой числовой оценке, понимать, что в большинстве случаев, особенно при рассмотрении крупных помещений, она носит ориентировочный характер.
По современным воззрениям принято разделять процесс отзвука, реверберации на две части: начальные, сравнительно редкие запаздывающие импульсы, и более уплотняющаяся во времени последовательность импульсов. Первую часть отзвука оценивают с позиций геометрической (лучевой) теории, вторую - с позиций статистической теории.
Геометрическая теория более приложима к анализу акустических процессов в помещениях больших размеров - концертных и театральных залах, крупных студиях. Оптимальные размеры зала (студии) определяют на основе анализа начальных отражений. При проектировании больших помещений расчет времени реверберации может дать результат, значительно отличающийся от реального, и главное - эта величина не позволяет полностью оценить акустическое качество помещения. В такой оценке главную роль играют начальные отражения. Правильное временное соотношение начальных отражений обеспечивает высокое качество звучания даже тогда, когда время реверберации отличается от оптимального.
Статистическая и волновая теории особенно применимы к помещениям сравнительно малых размеров, например к студиям звукового вещания и аудиториям различного назначения. Результаты этих теорий как бы дополняют друг друга. Первая дает возможность оценить время реверберации, вторая - рассчитать спектр собственных (резонансных) частот, скорректировать размеры помещения так, чтобы спектр собственных частот в области нижних частот был более равномерным.
Было бы очень интересно и важно объединить положения акустических теорий, создать единую теорию, объясняющую с общих позиций сложные акустические процессы, протекающие в помещениях разного назначения, разной формы и разных размеров. Но пока это не достигнуто, остается сознательно использовать существующие теории и добиваться с их помощью наилучших решений.
Рекомендуем обратиться к источникам, перечисленным в списке литературы, где можно найти много интересного и полезного для себя.
Литература
- Акустика:
Справочник / под ред. М.А. Сапожкова. - М.: Радио и связь, 1989.
- Бреховских
Л.М. Распространение волн в слоистых средах. - М.-Л.: Изд. АН СССР, 1958.
- Дрейзен
И.Г. Курс электроакустики, ч. 1. - М.: Связьрадиоиздат, 1938.
- Дрейзен
И.Г. Электроакустика и звуковое вещание. - М.: Связьиздат, 1951.
- Емельянов
Е.Д. Звукофикация театров и концертных залов. - М.: Искусство, 1989.
- Контюри
Л. Акустика в строительстве. - М.: Стройиздат, I960.
- Макриненко
Л.И. Акустика помещений общественного назначения. -- М.: Стройиздат, 1986.
- Морз
Ф. Колебания и звук. - М.-Л.: Гостехиздат, 1949.
- Сапожков
М.А. Звукофикация помещений. - М.: Связь, 1979.
- Скучик
Е. Основы акустики. - М.: Изд. иностр. лит., 1959.
- Стрэтт
Дж.В. (лорд Релей). Теория звука. - М.: ГИТТЛ, 1955.
- Фурдуев
В.В. Электроакустика. - М.-Л.: ОГИЗ-ГИТТЛ. 1948.
- Фурдуев
В.В. Акустические основы вещания. - М.: Связьиздат, I960.
- Фурдуев
В.В. Моделирование в архитектурной акустике // Техника кино и телевидения,
1966. N 10.
Все материалы библиотеки охраняются авторским правом и являются интеллектуальной собственностью их авторов.
Все материалы библиотеки получены из общедоступных источников либо непосредственно от их авторов.
Размещение материалов в библиотеке является их цитированием в целях обеспечения сохранности и доступности научной информации, а не перепечаткой либо воспроизведением в какой-либо иной форме.
Любое использование материалов библиотеки без ссылки на их авторов, источники и библиотеку запрещено.
Запрещено использование материалов библиотеки в коммерческих целях.
Учредитель и хранитель библиотеки «РусАрх»,
академик Российской академии художеств
Сергей Вольфгангович Заграевский